수학의 기초 4. 행렬

chapter 1. 행렬 기초

1. 개념

(1) 통계학과 행렬

행렬은 통계학에서 데이터를 표현하고 분석하는 데 핵심적인 도구로 사용된다. 행렬은 대규모 데이터의 구조를 간단히 표현하고, 계산을 효율적으로 수행하여 통계학에서 중요한 역할을 한다.

데이터 표현

데이터를 행렬로 저장하여 표 형식으로 표현한다. 다음은 관측값(행)과 변수(열)로 구성된 데이터 행렬이다.

\[X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}\]

연산의 간결화

여러 변수와 관측값 간의 관계를 분석할 때 행렬식으로 간단히 표현하고 행렬 연산을 이용하여 추정값을 계산한다.

$Y = X\beta + \epsilon$, OLS 추정=$\widehat{\beta} = (X'X)^{- 1}X'Y$

(2) 정의

행과 열로 배열된 숫자, 기호 또는 표현식의 직사각형 배열을 행렬이라 한다. 행의 차수는 $m$, 열의 차수는 $n$이다.

$A_{m \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$ (간편식) $A = \{ a_{ij}\}$

행렬의 각 셀을 원소 element라 한다.
행의 차수 $m = 1$인 행렬을 열 column 벡터이다.
열의 차수 $n = 1$인 행렬을 행 row 벡터이다.
행의 차수, 열의 차수 모두 1인 행렬을 스칼라 scalar이다.
행렬을 $n$-열벡터로 표현 : $A_{m \times n} = \begin{bmatrix} a_{1} & a_{2} & \cdots a_{n} \end{bmatrix}$
행렬을 $m$-헹벡터로 표현 : $A_{m \times n} = \left\lbrack \begin{array}{r} a_{1} \\ a_{2} \\ \cdots \\ a_{m} \end{array} \right\rbrack$

(3) 동일 행렬이란

행의 차수와 열의 차수가 같다. $A_{m \times n} = B_{m \times n}$
대응하는 모든 원소 값은 동일하다. $\{ a_{ij} = b_{ij}\} foralli,j$

2. 특수한 행렬

영행렬 zero matrix

행렬의 모든 원소가 0인 행렬입니다. 기호 : $0_{m \times n}or0$ 숫자 0에 해당된다.

정방행렬 square matrix

행렬의 행차수와 열차수가 동일한 행렬이다. 기호 : $A_{m \times m} = A_{m}$

대각행렬 diagonal matrix

대각원소를 제외한 모든 원소가 0인 정방행렬이다. 기호 : $A_{ij} = 0fori \neq j$, $diag(a_{11},a_{22},...,a_{mm})$

\[D = \begin{pmatrix} - 1 & 0 \\ 0 & 7 \end{pmatrix}\]

대각합 trace

대각행렬의 대각원소의 합을 대각합이라 한다. $tr(D) = 6$

단위행렬 identity matrix

정방행렬의 대각 원소가 모두 1이고 그외 원소는 0인 행렬로 숫자 1과 같은 역할을 한다. 기호 : $I_{ij} = \{\begin{array}{r} 1i = j \\ 0i \neq j \end{array}$ , $I_{m \times m}orI_{m}$

$A = \begin{bmatrix} 1 & 2 & 3 \\ 3 & 4 & 5 \end{bmatrix}$⇨ $A = \begin{bmatrix} 1 & 0 & 1 & 2 & 3 \\ 0 & 1 & 3 & 4 & 5 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} I & A \\ 0 & I \end{bmatrix}$

삼각행렬 triangular matrix

【상삼각행렬】 대각원소 아래 원소가 모두 0인 정방행렬이다. 기호 : $A_{ij} = 0fori > j$

【하삼각행렬】 대각원소 윗 원소가 모두 0인 정방행렬이다. 기호 : $A_{ij} = 0fori < j$

희소행렬 Sparse matrices

행렬 원소의 대부분이 0인 행렬을 의미하며 $nnz(A)$은 행렬 $A_{m \times n}$에서 0인 아닌 원소의 개수를 나타내며 $nnz(A)/(m \times n)$을 행렬의 밀도라 정의한다.

수학자 제임스 H. 윌킨슨(James H. Wilkinson)이 정의 : ”행렬이 충분히 많은 0 원소를 포함하고 있어 이를 활용하는 것이 유리한 경우, 그 행렬을 희소 행렬이라 한다.” 희소행렬은 컴퓨터에서 효율적으로 저장하고 조작할 수 있다.

영행렬 > 단위행렬 > 대각행렬 > 삼각행렬 : 대표적인 희소행렬

3. 행렬 놈

모든 원소의 제곱합의 양의 제곱근: $\parallel A \parallel = \sqrt{\overset{m}{\sum_{i}}\overset{n}{\sum_{j}}a_{ij}}$

행렬의 놈은 스칼라이며 행렬의 크기나 거리를 측정하며 행렬의 평균제곱근(Root Means Square)는 $RMS(A) = \frac{\parallel A \parallel}{\sqrt{mn}}$이다.

$\parallel A \parallel \geq 0$ 행렬 놈은 0보다 크거나 같다.
$\parallel cA \parallel = |c| \parallel A \parallel$
$\parallel A + B \parallel \leq \parallel A \parallel + \parallel B \parallel$
$\parallel A - B \parallel$ : 두 행렬의 유사성(거리)을 나타낸다.
$\parallel A \parallel = \parallel A^{T} \parallel$ : 원행렬 놈과 전치행렬 놈은 동일하다.

4. 전치

전치 transpose는 행과 열을 서로 바꾸는 연산: $(A^{T})_{ij} = A_{ji}$

$(A^{T})^{T} = A$ : 전치 행렬을 다시 전치하면 원래 행렬이 된다.
$(A + B)^{T} = A^{T} + B^{T}$ : 행렬 합의 전치는 각 행렬의 전치 합과 같다.
$(cA)^{T} = cA^{T}$ : 스칼라 곱의 전치는 스칼라 곱과 같다.
$(AB)^{T} = B^{T}A^{T}$ : 행렬 곱의 전치는 각 행렬의 전치의 순서를 바꾼 곱과 같다.

원행렬과 전치행렬과 동일한 행렬은 대칭행렬이다. $A = A^{T}$

chapter 2. 행렬 연산

1. 행렬 합 연산

행렬의 합을 구하는 경우 두 행렬의 차수는 동일해야 하며(conformable for addition/substraction: 합 연산 적합) 각 행렬에서 대응하는 원소들의 합을 그 위치에 적으면 된다.

\[(A + B)_{m \times n} = \{ a_{ij} + b_{ij}\}\]

\[(A + B)_{m \times n} = \begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\ a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn} \end{bmatrix}\]

\[A = \begin{bmatrix} 1 & 3 & 5 \\ 7 & 3 & 1 \end{bmatrix}$, $B = \begin{bmatrix} 1 & 0 & 1 \\ - 1 & 1 & 0 \end{bmatrix}$ ⇢ $A + B = \begin{bmatrix} 2 & 3 & 6 \\ 6 & 4 & 1 \end{bmatrix}\]

성질

교환법칙 Commutativity : $A + B = B + A$
결합법칙 Associativity : $A + (B + C) = (A + B) + C = A + B + C$
영행렬과 합 : $A + 0 = 0 + A = A$
합의 전치 : $(A + B)^{T} = A^{T} + B^{T}$

2. 스칼라-행렬 곱하기

행렬 모든 원소에 스칼라 곱을 하여 결과는 원행렬과 동일한 차수의 행렬이다. (기호) $cA = \{ ca_{ij}\} = Ac$ 다음의 성질을 갖는다.

$(cA)^{T} = cA^{T}$
$(c + d)A = cA + dA$

3. 행렬x벡터 곱하기

행렬 $A_{m \times n}$와 행벡터 $x_{n}$ 곱 연산은 다음과 같이 정의되며 결과는 행벡터 $y_{m \times 1} = A_{m \times n}x_{n \times 1}$이며 차수는 $m$이다.

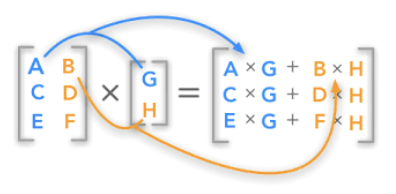
연산 가능

앞의 행렬($A_{m \times n}$)의 열차수와 뒤의 행벡터($x_{n}$) 행차수가 동일해야 한다.

행 측면

행렬 $A$의 $i$-번째 행벡터을 $a_{i}^{T}$라 하면 $y_{i} = a_{i}^{T}x$(내적)이다.

열 측면

$A$의 $k$-번째 열벡터을 $a_{k}$라 하면 $y = x_{1}a_{1} + x_{2}a_{2} + + ... + x_{n}a_{n}$.

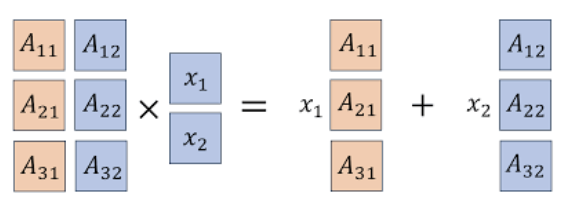
행렬 $A$의 열벡터 선형독립이다

만약 $x = 0$인 경우에만 $Ax = 0$이 성립하면, 열벡터는 선형독립이다.

활용

행렬 $A$가 영행렬이면 $Ax = 0$는 영벡터이다.
행렬 $A$가 단위행렬이면 $Ax = x$이다.
행렬 $A$의 $j$-번째 열벡터는 $Ae_{j} = a_{j}$이다.
행렬 $A$의 $i$-번째 행벡터는 $(A^{T}e_{i})^{T}$이다.

예제

(예측데이터 행렬) Feature matrix $X_{N \times n}$는 $N$개의 객체에 대한 특성 $n$-벡터, 객체들에 대한 가중치 $w$-벡터(차수 $N$)라 하자. $X^{T}w$는 객체들에 대한 가중 점수 벡터이다.

(포트폴리오 자산 수익율) 포트폴리오 자산 수익율 행렬 $R_{T \times n}$($T$ 기간 동안 $n$개의 자산의 수익률)이라 하고 $w$을 포트폴리오 $n$-벡터라 하면 $Rw$는 $T$기간 포트폴리오 수익률이다.

(오디오 믹싱) $A$의 $k$개 열이 길이 $T$의 오디오 신호나 트랙을 나타내는 벡터들이고, $w$가 $k$-벡터인 경우를 가정하면 $Aw$는 오디오 신호들을 믹싱한 결과를 나타내는 $T$-벡터이다.

(문서 점수화) 검색 엔진은 검색 쿼리를 기반으로 w를 선택하여 문서의 점수를 예측한다. $A$는 $N \times n$크기의 문서-단어 행렬로, $N$개의 문서가 $n$개의 단어 사전을 사용하여 단어의 출현 빈도, $w$는 $n$-벡터로, 단어 사전 내 단어들에 대한 가중치로 $Aw$는 $N$-벡터로, 각 문서의 점수를 나타낸다.

4. 행렬x행렬 곱하기

(1) 정의

행렬을 곱하기 위해서는 앞 행렬의 열 차수와 뒤 행렬의 행의 차수와 일치해야 곱이 가능하다. conformable for product 결과의 차수는 앞 행렬의 행 차수, 뒤 행렬의 열 차수를 갖는다.

$A_{m \times n}B_{n \times p} = (AB)_{m \times p}$

$A = \{ a_{ij}\}$, $B = \{ b_{ij}\}$ ⇢ $AB = \{\overset{n}{\sum_{k = 1}}a_{ik}b_{kj}\}$

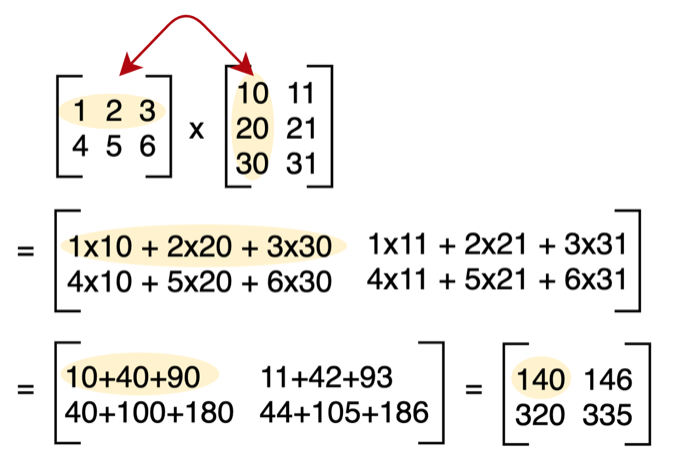
(2) 곱의 성질

결합 associate 법칙: $(AB)C = A(BC)$
배분 distribution 법칙: $A(B + C) = AB + AC$
전치 : $(AB)^{T} = B^{T}A^{T}$
$(A + B)(C + D) = AC + AD + BC + BD$
$y^{T}(Ax) = (y^{T}A)x = (A^{T}y)^{T}x$

(3) 행렬의 거듭제곱

\[A^{2} = AA$, $A^{3} = AAA$, $A^{4} = AAAA \cdots \]

directed graph

인접 adjacency 행렬을 다음과 같이 정의하자.

\[A_{ij} = \{\begin{array}{r} \text{1 there is a edge from vertex j to vertex i} \\ \text{0 otherwise} \end{array}\]

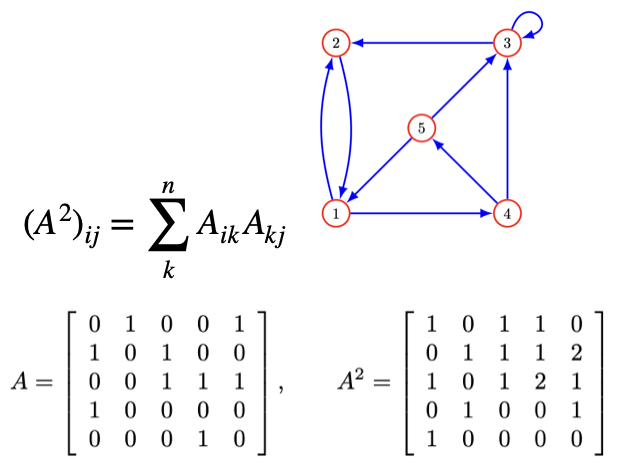
멱등행렬 idempotent

자신의 행렬 곱이 자신이 되는 행렬을 멱등행렬이라 한다. $M^{2} = M^{3} = ... = M$ 자신의 곱이 연산 가능해야 하므로 멱등행렬이려면 정방행렬이어야 한다.

5. QR 분해, Q는 직교행렬, R은 상삼각행렬

(1) 직교행렬 orthonormal matrix

열벡터 $A_{m \times n}$의 n-벡터 $a_{1},a_{2},...,a_{m}$들이 orthonomal 하면, 즉 $A^{T}A = I$을 만족하는 행렬을 직교정규행렬이라 한다.만약 $A_{m \times n}$는 직교정규행렬, $x,y$는 n-벡터라 하고 $f:R^{n} \rightarrow R^{m}$ 함수가 $z$를 $Az$로 매핑한다고 가정하자.

$\parallel Ax \parallel = \parallel x \parallel$ : 함수 $f$는 놈을 보존한다.
$(Ax)^{T}(Ay) = x^{T}y$ : 함수 $f$는 두 벡터의 내적을 보존한다.
$\angle(Ax,Ay) = \angle(x,y)$ : 함수 $f$는 두 벡터의 각도을 보존한다.

【recall】 Gram-Schmidt 알고리즘

만약 벡터들이 선형 독립이라면, Gram–Schmidt 알고리즘은 다음과 같은 속성을 가진 직교정규 벡터 $q_{1},q_{2},...,q_{k}$ 을 생성한다.

(2) QR분해 $A = QR$

행렬 $A_{n \times k}$의 n-벡터 $a_{1},a_{2},...,a_{k}$가 선형 독립인 행렬이다. 여기에 Gram-Schmidt 알고리즘을 적용하여 얻은 직교정규 벡터 $q_{1},q_{2},...,q_{k}$으로 직교정규 행렬 $Q$을 생성하자. $Q^{T}Q = I$이다.

$a_{i}$와 $q_{i}$의 관계식 : $a_{i} = (q_{1}^{T}a_{i})q_{1} + \cdots + (q_{i - 1}^{T}a_{i})q_{i - 1} + \parallel {\overset{˜}{q}}_{i} \parallel q_{i}$

이를 다시 쓰면 $a_{i} = R_{1i} + \cdots + R_{ii}q_{1}$이다. $R_{ij} = q_{i}^{T}a_{j}fori < j$, $R_{ij} = 0fori > j$, 그리고$R_{ii} = \parallel {\overset{˜}{q}}_{i} \parallel$

그러므로 $A_{n \times k}$ (열이 독립인 행렬)은 직교정규 행렬 $Q_{n \times k}$과 $R_{k \times k}$ 상삼각행렬로 분해된다.

(3) QR 분해 활용

선형 시스템의 해 구하기, 최소자승 문제, 정규방정식 문제

선형 방정식 $Ax = b$를 푸는 데 사용될 수 있다. $A = QR$로 분해하면 $QRx = b$가 되고 $R_{x} = Q^{T}b$이므로 $R$이 상삼각 행렬이므로 후진 대입을 사용하여 해, $x$를 효율적으로 구할 수 있다.

고유값 계산

$QR$ 알고리즘을 이용하여 특정 행렬의 고유값을 계산할 수 있다. $QR$ 분해를 사용한 고유값 계산 알고리즘은 변환 행렬을 상삼각 행렬로 변환하고, 이로부터 고유값을 추출한다.

행렬의 특성 분석

$QR$ 분해는 행렬의 특성을 분석하는 데 도움을 준다. 예를 들어, 행렬의 계수(rank)를 결정하거나, 행렬이 정칙인지 (역행렬이 존재하는지) 파악하는데 사용될 수 있다.

import numpy as np
# 행렬 A 정의
A = np.array([[1, 1], [1, -1], [1, 1]])
# QR 분해
Q, R = np.linalg.qr(A)
# 결과 출력
print("Q:")
print(Q)
print("\nR:")
print(R)

【결과】 Q: [[-0.57735027 0.40824829] [-0.57735027 -0.81649658] [-0.57735027 0.40824829]]

R: [[-1.73205081 -0.57735027] [ 0. 1.63299316]]

6. 역행렬

(1) 왼쪽 오른쪽 역행렬

만약 $XA = I$ 만족하는 $X$가 존재하면 A는 left-invertible 이라 한다. 동일하게 $AX = I$ 만족하는 $X$가 존재하면 A는 right-invertible 이라 한다.

left-invertible과 열 벡터는 선형독립

만약 행렬 $A$가 left-inverse 행렬 $C$ 갖는다면 행렬 $A$의 열벡터는 선형 독립이다.

【증명】 $Ax = 0$을 만족하는 $x = 0$이므로 $A$의 열벡터는 선형 독립이다. $0 = CAx = Ix = x$

left-invertible 행렬($C$) 갖는 $A$ 선형방정식 $Ax = b$ 해 구하기

\[C_{m \times m}A_{m \times n}x_{n} = C_{n \times n}b_{n} \rightarrow x_{n} = C_{n \times n}b_{n}\]

right-invertible과 행 벡터는 선형독립

만약 행렬 $A$가 right-inverse 행렬 $B$ 갖는다면 행렬 $A$의 행벡터는 선형 독립이다.

left, right invertible 관계

행렬 $A$의 right inverse $B$을 가지면 $B^{T}$는 $A^{T}$의 left inverse 행렬이다.

【증명】 $AB = I \rightarrow (AB)^{T} = I^{T} \rightarrow B^{T}A^{T} = I$

right-invertible 행렬($B$) 갖는 $A$ 선형방정식 $Ax = b$ 해 구하기

해는 $x = Bb$이다. 【증명】 $Ax = A(Bb) = (AB)b = b$

(2) 역행렬 구하기

행렬의 역수 개념이다. 3에 어떤 수를 곱하면 1이 될까? 답은 $\frac{1}{3}$(역수)이다. 마찬가지로 행렬 $A$에 무엇을 곱하면 항등행렬 $I$가 될까? 이를 역행렬이라 한다. $AA^{- 1} = A^{- 1}A = I$

행렬식 determinant

행렬식은 정방행렬에서만 계산되며 결과는 스칼라이다. 기호는 $det(A)$혹은 $|A|$으로 표현한다. 다음은 행렬식 계산 방법이다.

$A_{2 \times 2} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ ⇢ $det(A) = ad - bc$ $A = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}$, $|A| = - 2$

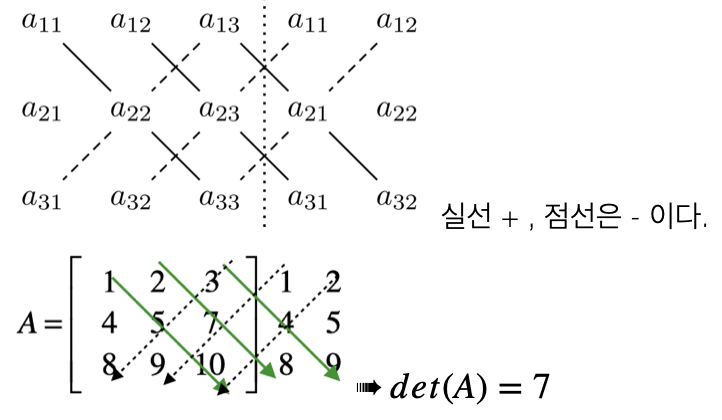
행렬식 성질

$|A^{T}| = |A|$
$|AB| = |BA|$
$|AB| = |A||B|$
한 열에 $k$배 한 후 다른 열에 더하여도 행렬식은 변하지 않는다.
한 열이 다른 열의 선형결합으로 표현된다면 행렬식은 0이다.

소행렬 minor

$i$행, $j$열은 제외한 행렬을 소행렬($M_{ij}$)이라 하고 소행렬의 행렬식을 소행렬식($|M_{ij}|$)이라 한다. 일반적으로 소행렬은 소행렬식을 의미한다.

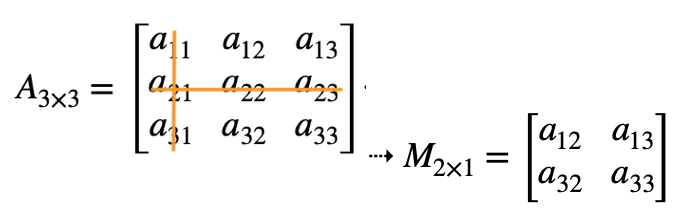
여인수 cofactor

$C_{ij} = ( - 1)^{i + j}|M_{ij}|$을 여인수라 한다. 여인수를 이용하여 다음과 같이 행렬식을 구할 수 있다.

$|A_{n \times n}| = \overset{n}{\sum_{i = 1}}a_{ij}( - 1)^{i + j}|M_{ij}|$,$|A_{n \times n}| = \overset{n}{\sum_{j = 1}}a_{ij}( - 1)^{i + j}|M_{ij}|$

여인수 행렬 / 수반행렬 adjoint

$C_{ij} = \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix}$⇢ $adj(A) = \begin{bmatrix} C_{11} & C_{21} & C_{31} \\ C_{12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \end{bmatrix}$

역행렬 구하기

정방행렬 $A$에 대하여 $AB = BA = I$을 만족하는 행렬 $B$를 $A$의 역행렬이라 하며 $A^{- 1}$로 표현한다.

\[A^{- 1} = \frac{1}{|A|}adj(A)\]

역행렬 성질

역행렬은 유일하고 $(A^{- 1})^{- 1} = A$이 성립한다.
$(AB)^{- 1} = B^{- 1}A^{- 1}$
$(A^{T})^{- 1} = (A^{- 1})^{T}$
$|A^{- 1}| = \frac{1}{|A|}$

계수 rank

차수가 $n$인 정방행렬 $A_{n \times n}$의 열벡터에 대하여 $k_{1}\underset{¯}{a_{1}} + k_{2}\underset{¯}{a_{2}} + ... + k_{n}\underset{¯}{a_{n}} = \underset{¯}{0}$ 방정식이 모든 상수 $k_{j}$가 0일 때만 만족하는 경우 열벡터($\underset{¯}{a_{j}}$)는 선형독립 linearly independent이라 한다. 만약 적어도 0이 아닌 상수가 하나라도 존재하면 종속이라 한다.

정방행렬 $A_{n \times n}$에 대하여 선형 독립인 행의 개수와 열의 개수 중 작은 것을 행렬의 계수라 한다. 행렬의 차수와 계수가 동일하면 이를 full-rank라 한다.

행렬 $A_{n \times n}$에 대하여 각 열은 동일하다.

역행렬 $A^{- 1}$은 존재한다.	역행렬 $A^{- 1}$은 존재하지 않는다.
행렬식은 0이 아니다. $det(A) \neq 0$	행렬식은 0이다. $det(A) = 0$
full rank이다. $rank(A) = n$	full rank 아니다. $rank(A) < n$
행렬 A는 non-singular이다.	행렬 A는 singular이다.
$AX = \underset{¯}{b}$ 해가 존재한다.	$AX = \underset{¯}{b}$ 해가 존재하지 않는다.

chapter 3. 행렬 활용

1. 연립방정식 해 구하기 $Ax = b$

(1) $QR$ 분해 이용

행렬 $A$을 $QR$분해 한다. $A = QR$
$Q^{T}b$을 구한다.
후진 제거 방법으로 $Rx = Q^{T}b$을 구한다.

(2) 역행렬 계산 $A^{- 1}$

행렬 $A$의 역행렬 $A^{- 1}$을 이용하여 $\widehat{x} = A^{- 1}b$ 해를 구한다.

2. 최소자승법

(1) 최소자승 문제

$A_{m \times n}x_{n} = b_{m}$(단 $m > n$) 선형방정식에서는 $m$개의 방정식이 $n$개 변수보다 많으므로 $b$가 행렬 $A$의 열의 선형결합일 때만 해를 갖는다. $b$을 어떻게 구할 것인가? 잔차 $r = Ax - b$최소화 하는 $x$을 찾는 것을 최소자승법이라 한다. $minmize \parallel Ax - b \parallel$ $2x_{1} = 1, - x_{1} + x_{2} = 0,2x_{2} = - 1$ : 방정식 3개, 미지수 2개

$Ax = b$: $\begin{bmatrix} 2 & 0 \\ - 1 & 1 \\ 0 & 2 \end{bmatrix}\left\lbrack \begin{array}{r} x_{1} \\ x_{2} \end{array} \right\rbrack = \begin{bmatrix} 1 & 0 & 1 \end{bmatrix}$

(2) 최소자승 해 구하기

$minmizef(x) = \parallel Ax - b \parallel^{2}$ 해 $\widehat{x}$는 $\frac{\partial f}{\partial x_{i}}(\widehat{x}) = 0,i = 1,2,...,n$을 만족하므로 $\nabla f(x) = 2A^{T}(Ax - b)$ 방정식에서 $\nabla f(\widehat{x}) = 0$이다. 그러므로 최소자승 해는 $\widehat{x} = (A^{T}A)^{- 1}A^{T}b$이다.

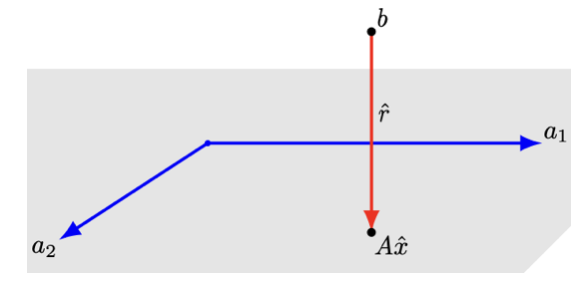
$A = QR$ 분해 이용

$Ax = b$의 최소자승 해는 $\widehat{x} = R^{- 1}Q^{T}b$이다.

\[RMS = \sqrt{\parallel b - A\widehat{x} \parallel^{2}}\]

매출 광고

행은 사회인구학적 특성 10개이고 열은 3개 광고 채널이고 $R_{ij}$는 $i$-사회인구학적특성의 $j$-광고채널의 1달러당 노출회수(단위: 1000)이다. 만약 각 사회인구학적 특성 집단별로 노출회수를 $10^{3}$으로 할 경우 광고비는 얼마?

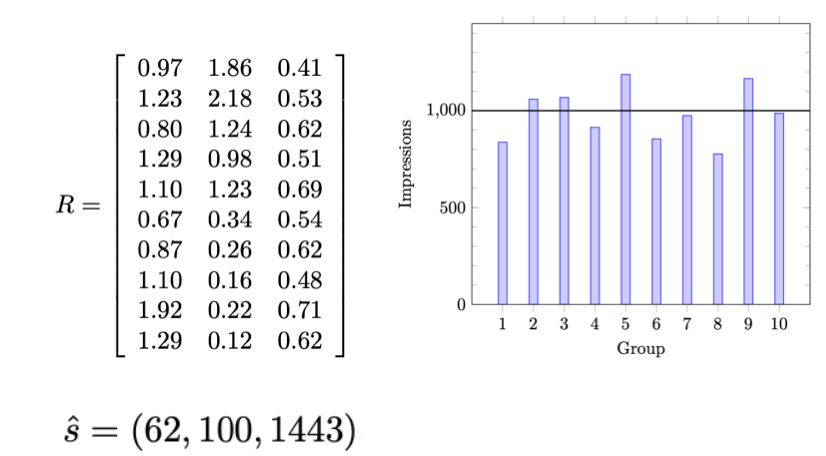
$R_{10 \times 3}x_{3} = 10^{3}1_{3}$에 대한 최소자승해는 $\widehat{x} = (62,100,1443)$으로 각 채널당 광고비이다. $RMS = 13.2\%$이다.

(3) 최소자승 데이터 적합

$n$-벡터 $x$(feature 벡터, 독립변수), 스칼라 $y$는 다음 근사 함수 관계가 있다고 하자. $f:R^{n} \rightarrow R,y \approx f(x)$

데이터

\[x^{(1)},x^{(2)},...,x^{(N)},y^{(1)},y^{(2)},...,y^{(N)}\]

모델 관측치 개수 $N$, 예측변수 개수 $p$

feature 벡터와 스칼라 벡터 사이 함수 관계는 $f$(예측함수)은$y \approx \widehat{f}(x),where\widehat{f}:R^{n} \rightarrow R$

$\widehat{f}(x)$는 파라미터 $p$-벡터 $\theta$의 선형 함수이다.

$\widehat{f}(x) = \theta_{1}f_{1}(x) + \theta_{2}f_{2}(x) + \cdots + \theta_{p}f_{p}(x)$, where $f_{i}:R^{n} \rightarrow R$

예측값과 예측오차

$y^{(i)} \approx \widehat{f}(x^{(i)})$이고 예측오차(잔차)는 $r^{(i)} = y^{(i)} - {\widehat{y}}^{(i)}$이다.

최소자승 모델 적합

$i = 1,2,\cdots,N,j = 1,2,\cdots,p$

$y^{d} = (y^{(1)},y^{(2)},...,y^{(N)})$, ${\widehat{y}}^{d} = ({\widehat{y}}^{(1)},{\widehat{y}}^{(2)},...,{\widehat{y}}^{(N)})$

예측오차합 $\parallel r^{d} = y^{d} - {\widehat{y}}^{d} \parallel^{2}$을 최소화 하는 모수 $\theta$을 찾는다.

\[{\widehat{y}}^{(i)} = A_{i1}\theta_{1} + A_{i1}\theta_{2} + \cdots + A_{i1}\theta_{p},whereA_{ij} = {\widehat{f}}_{j}(x^{(i)})\]

${\widehat{y}}^{d} = A\theta$이므로 $\parallel r^{d} \parallel^{2} = \parallel y^{d} - A\theta \parallel^{2}$이다.

최소자승 추정 : $\widehat{\theta} = (A^{T}A)^{- 1}A^{T}y^{d}$

상수항(절편) 있는 선형함수 최소자승 추정

모든 $x$에 대하여 $f_{1}(x) = 1$을 갖는 상수함수를 고려하자. $\widehat{f}(x) = \theta_{1}$이고 $A_{(N \times 1)} = 1_{N}$이다.

\[\widehat{\theta} = (A^{T}A)^{- 1}A^{T}y^{d} = N^{- 1}1^{T}y^{d} = avg(y^{d})\]

(4) 다항식 적합

모형

$\widehat{f}(x) = \theta_{1} + \theta_{2}x + \cdots + \theta_{p}x^{p - 1}$

\[A = \begin{bmatrix} 1 & x^{(1)} & \cdots & (x^{(1)})^{p - 1} \\ 1 & x^{(2)} & \cdots & (x^{(2)})^{p - 1} \\ \cdots & & & \\ 1 & x^{(N)} & \cdots & (x^{(N)})^{p - 1} \end{bmatrix}\]

Piecewise-Linear Fit 분절선형 적합

절단점 식별: 선의 기울기가 변하는 지점을 결정한다.

선형 구간 적합: 절단점으로 분리된 각 데이터 구간에 선형 모델을 적합한다.

구간 결합: 절단점에서 구간함수를 연결하여 연속적인 분절선형 함수를 형성한다.

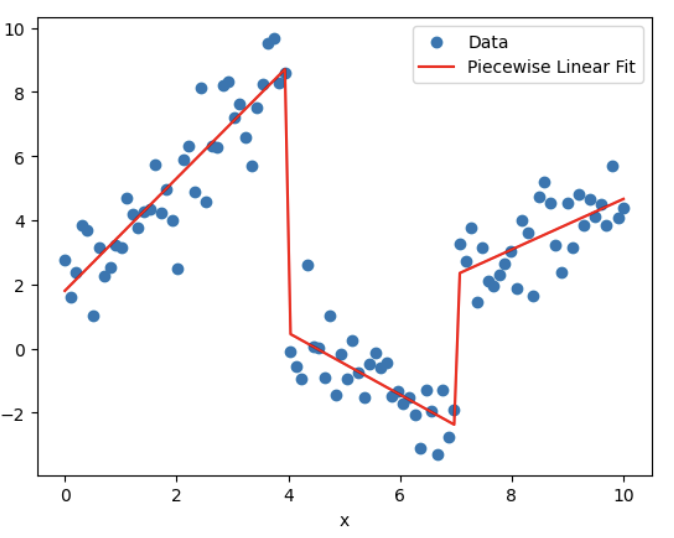
# Piecewise-Linear Fit
import numpy as np
# 합성 데이터 생성
np.random.seed(0)
x = np.linspace(0, 10, 100)
y = np.piecewise(x, [x < 4, (x >= 4) & (x < 7), x >= 7],[lambda x: 2 * x + 1 + np.random.normal(size=len(x)),lambda x: -x + 5 + np.random.normal(size=len(x)),lambda x: 0.5 * x - 1 + np.random.normal(size=len(x))])
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# 분절선형 함수 정의
def piecewise_linear(x, x0, x1, y0, y1, y2, k1, k2, k3):
    conds = [x < x0, (x >= x0) & (x < x1), x >= x1]
    funcs = [lambda x: k1 * x + y0, lambda x: k2 * x + y1, lambda x: k3 * x + y2]
    return np.piecewise(x, conds, funcs)
# 초기 파라미터 추정값
p0 = [4, 7, 1, 5, -1, 2, -1, 0.5]
# 데이터를 분절선형 함수에 적합시킴
params, _ = curve_fit(piecewise_linear, x, y, p0=p0)
# 데이터를 적합한 결과와 함께 플로팅
x_fit = np.linspace(0, 10, 100)
y_fit = piecewise_linear(x_fit, *params)

plt.scatter(x, y, label='Data')
plt.plot(x_fit, y_fit, color='red', label='Piecewise Linear Fit')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

3. 간선행렬

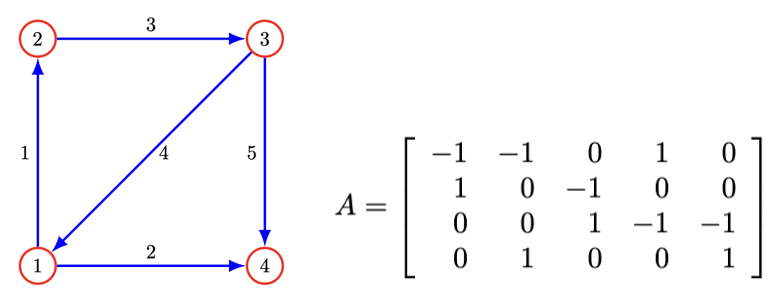
간선 행렬 Incidence matrix은 그래프 이론에서 사용되는 개념으로, 정점과 vertices 간선 edges, nodes 사이의 관계를 나타내는 행렬입니다.

간선 행렬 $G_{n \times m}$은 정점이 $n$개, 간선이 $m$개이다.

$A_{ij} = 1$ : 정점 $i$와 간선 $j$와 연결되어 있고 정점 $i$는 끝 정점이 아니다.

$A_{ij} = 1$ : 정점 $i$와 간선 $j$와 연결되어 있고 정점 $i$는 끝 정점이다.

$A_{ij} = 0$ : 정점 $i$와 간선 $j$와 연결되어 않음

4. 네트워크

만약 $x$가 네트워크에서의 흐름을 나타내는 $m$-벡터라면, $x_{j}$는 간선 $j$를 통한 흐름으로 해석된다. 여기서 양의 값은 흐름이 간선 $j$의 방향으로 이동하고, 음의 값은 흐름이 간선 $j$의 반대 방향으로 이동함을 의미한다. 네트워크에서 간선이나 링크의 방향은 흐름의 방향을 지정하지 않고 그저 흐름 flow의 방향을 고려하는 것을 나타내는 것이다.

네트워크에서의 흐름 보존은 흐름이 노드와 간선을 통해 어떻게 이동하는지를 설명하며, 각 노드로 들어오는 총 흐름이 노드에서 나가는 총 흐름과 같음을 보장한다.

네트워크 구조를 나타내는 $G_{n \times m}$를 사용하여

$y = Gx$는 각 노드로 들어오는 순흐름을 나타내는 $n$-벡터이다.

$y_{i}$는 $i$-노드로 들어오는 총 흐름에서 $i$-노드에서 나가는 총 흐름을 뺀 값이다 즉, $i$-노드에서의 흐름 잉여 surplus이다.

요약하면, $y = Gx$는 네트워크 이론에서의 흐름 보존 원칙을 요약한 것으로, 각 요소 $y_{i}$는 노드 $i$에서의 순 흐름 균형을 나타내며 모든 들어오는 흐름과 나가는 흐름을 고려한다.

만약 $Gx = 0$인 상태를 각 노드에서 총 들어오는 흐름과 총 나가는 흐름이 일치하기 때문에 흐름 보존이 일어난다고 말한다.

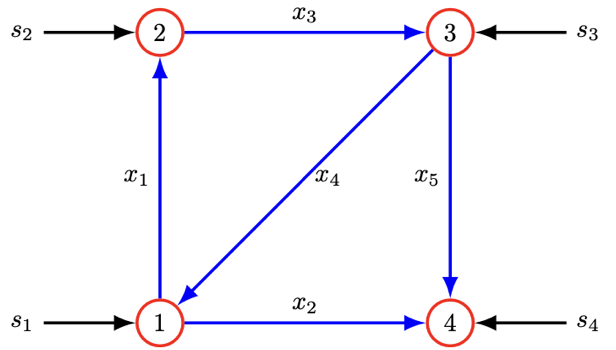
위의 그래프에 의해 나타낸 네트워크에서 $x = (1, - 1,1,0,1)$이다. 소스는 source 노드에서 네트워크로 들어오거나 나가지만, 간선을 따라 흐르지는 않습니다. 위 그림에서 보여지는 것처럼 이러한 흐름들은 5-벡터 4소스로 나타낸다. $s_{i}$를 노드 $i$에서 외부에서 네트워크로 들어오는 흐름으로 생각할 수 있다. 즉, 어떤 간선을 통해서도 들어오지 않는 것이다. $s_{i} > 0$일 때 외부흐름은 소스라고 부르며 $s_{i} < 0$일 때 외부흐름은 싱크라고 부른다.

소스 포함된 흐름 보전 : $Ax + s = 0$

5. 선형함수 모델

필드에서 발생하는 많은 함수나 변수 간의 관계는 선형 또는 아핀 함수로 근사될 수 있는데, 두 변수 집합 간의 선형 함수를 모형(model) 또는 근사(approximation) 값으로 정의한다.

(1) 수요의 가격 탄력성(Price elasticity of demand)

가격이 n개의 상품(서비스)에 의해 결정되는 n-벡터 p로 주어지고, 상품에 대한 수요가 n-벡터 d로 주어진다. n-벡터 $\delta^{price}$를 가격변화 벡터라 하면 $\delta^{price} = \frac{(p_{i}^{new} - p_{i})}{p_{i}}$라 하자($p^{new}$는 새로운 가격 n-벡터). n-벡터 $\delta^{dem}$를 수요변화 벡터라 하면 $\delta^{dem} = \frac{(d_{i}^{new} - d_{i})}{d_{i}}$라 하자. $\delta^{dem} = E^{d}\delta^{price}$, $E^{d}$는 ($n \times n$) 수요 탄력성 행렬이다.

$E_{11}^{d} = - 0.4$, $E_{21}^{d} = 0.2$ 가정해 보자. 이는 첫 번째 상품의 가격이 1% 증가할 때, 다른 가격은 동일한 상태에서 첫 번째 상품의 수요가 0.4% 감소하고, 두 번째 상품의 수요가 0.2% 증가할 것임을 의미한다. 두 번째 상품은 첫 번째 상품의 부분 대체품으로 작용하고 있다.

(2) 탄성 변형 Elastic deformation

f 를 구조물에 작용하는 특정 위치(및 방향)에 대한 힘(하중)을 나타내는 n-벡터라고 합시다. 구조물은 하중으로 인해 약간 변형될 것입니다. d는 하중으로 인해 구조물의 m개 지점에서 발생하는 변위(특정 방향으로)를 나타내는 m-벡터입니다. 변위와 하중 사이의 관계는 선형으로 잘 근사된다. d= Cf 여기서 C 는 m × n 컴플라이언스(compliance) 행렬이고 C 의 항목의 단위는 m/N입니다.

(3) 테일러 근사

함수 $f:R^{n} \rightarrow R^{n}$이 1차 미분이 가능하다고 하면 테일러 근사는 $\widehat{f}(x)_{i} = f_{i}(z) + \triangledown f_{i}(z)^{T}(x - z)$, 단 n-벡터 $z$는 n-벡터 $x$와 가까운 값이다.

$\widehat{f}(x) = f(z) + Df(z)(x - z)$, 단.$Df(z)_{ij} = \frac{\partial f_{i}}{\partial x_{i}}(z),i = 1,...,m,j = 1,...,n$

(4) 회귀모형

표본 크기 $N$, 예측변수 벡터 $x^{(1)},x^{(2)},...,x^{(N)}$이다. $i$-개체의 예측치는 ${\widehat{y}}^{(i)} = (x^{(i)})^{T}\beta + v,i = 1,2,...,N$이다. 그리고 $X$는 예측변수 행렬, $y$는 목표변수 벡터이다.

잔차는 $r^{(i)} = y^{(i)} - {\widehat{y}}^{(i)}$.
절편 없는 회귀모형 : ${\widehat{y}}^{d} = X^{T}\beta + v1$
절편 회귀모형 : ${\widehat{y}}^{d} = \left\lbrack \begin{array}{r} 1^{T} \\ X \end{array} \right\rbrack^{T}\left\lbrack \begin{array}{r} v \\ \beta \end{array} \right\rbrack$

6. 선형 동적 시스템

시간에 따라 변하는 상태 벡터의 선형 관계를 설명하는 모델로 시스템의 현재 상태가 다음 상태를 예측할 수 있는 간단한 수학적 구조이다. $x_{t}$가 현재 상태인 $x_{1},x_{2},\cdots$ n-벡터 시계열이라 하자. 예를 들면, $(x_{5})_{3}$ 3번째 포트폴리오의 5일째 주가가 된다.

(1) 입력이 포함된 선형 동적 시스템

\[x_{t + 1} = A_{t}x_{t} + B_{t}u_{t},t = 1,2,...\]

$u_{t}$ 는 시간 t 에서의 입력벡터이고 .B 는 입력행렬로, 입력 $u_{t}$(외생 변수라고도 함)가 상태 벡터 $x_{t}$에 미치는 영향을 설명한다.

(2) $K$-Markov 모형

\[x_{t + 1} = A_{1}x_{t} + \cdots + A_{K}x_{t - K + 1},t = K,K + 1,...\]

상태 State : 시스템이 존재할 수 있는 모든 가능한 상태들의 집합. 예를 들어, 날씨 예측 모델에서 상태는 ”맑음”, ”흐림”, ”비” 등이 될 수 있다. 시스템이 가질 수 있는 모든 상태들의 집합을 상태 공간 $S$라 한다.
상태 전이 State Transition : 한 상태에서 다른 상태로의 전이. 상태 전이는 확률적으로 이루어지며 $P_{i}$는 초기상태 확률분포이다.
전이 확률 Transition Probability : 현재 상태에서 다음 상태로 전이될 확률을 나타낸다. 이는 $P(x_{t + 1} = s_{j}|x_{t} = s_{i})$로 표현되며, 현재 상태 $i$에서 다음 시점에 상태 $j$로 전이될 확률이다.

# Markov model
import numpy as np
# 전이 행렬 정의
P = np.array([[0.8, 0.2],[0.4, 0.6]])
# 초기 상태 분포 정의
pi_0 = np.array([0.6, 0.4])
# 상태 이름 정의
states = ["Sunny", "Rainy"]
# 시뮬레이션을 위한 시간 단계 수
num_steps = 10
# 초기 상태 선택
current_state = np.random.choice(states, p=pi_0)
print(f"Day 0: {current_state}")
# 시뮬레이션 시작
for t in range(1, num_steps + 1):
    if current_state == "Sunny":
        next_state = np.random.choice(states, p=P[0])
    else:
        next_state = np.random.choice(states, p=P[1])
    print(f"Day {t}: {next_state}")
    current_state = next_state

7. 인구 동태

100-벡터 $(x_{t})_{i}$는 $t$ 시점의 $(i - 1)$세 인구이다. 100- 벡터 $b$의 $b_{i}$는 $(i - 1)$의 평균 출생율이다. 가임 연령을 고려하면 벡터 b의 원소는$b_{I} = 0fori < 13ori > 50$이다. 만약 사망, 이민 없다고 가정하면 내년 0세 인구는 $(x_{t + 1})_{1} = b^{T}x_{t}$이다.

나이 $i$세 $(t + 1)$ 시점의 인구수는 다음과 같다. $d_{i}$는 $i$세 사망자수이다.$(x_{t + 1})_{i + 1} = (1 - d_{i})(x_{t})_{i},i = 1,2,\cdots,99$. 최종적으로 인구 동태 모형은 $x_{t + 1} = Ax_{t},t = 1,2,\cdots$이다.

전이행렬 $A$

\[A = \begin{bmatrix} b_{1} & b_{2} & b_{3} & \cdots & b_{98} & b_{99} & b_{100} & \\ 1 - d_{1} & 0 & 0 & \cdots & 0 & 0 & 0 & \\ 0 & 1 - d_{2} & 0 & \cdots & 0 & 0 & 0 & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \\ 0 & 0 & 0 & \cdots & 1 - d_{98} & 0 & 0 & \\ 0 & 0 & 0 & \cdots & & 0 & 1 - d_{99} & 0 \end{bmatrix}\]

이민을 고려한 인구 동태 모형

$x_{t + 1} = Ax_{t} + u_{t},t = 1,2,\cdots$, 벡터 $(u_{t})_{i}$는 t-시점에 나이 $(i - 1)$세의 순이민자수이다.

간단한 인구동태 방정식

\[P_{t + 1} = P_{t} + (B_{t} - D_{t}) + M_{t}\]

$P_{t}$ : $t$ 시점의 인구수, $B_{t}$ : $t$ 시점의 출생자수, $D_{t}$ : $t$ 시점의 사망자수, $M_{t}$ : $t$ 시점의 순 이민자수

# 인구동태모형
import numpy as np
import matplotlib.pyplot as plt
# 초기 인구와 파라미터 설정 미국 23년 기준
initial_population = 330_000_000
birth_rate = 12.4 / 1000
death_rate = 8.9 / 1000
annual_net_migration = 1_000_000
years = 10
# 인구 예측을 위한 배열 초기화
population = np.zeros(years + 1)
population[0] = initial_population
# 연도별 인구 예측
for t in range(1, years + 1):
    births = population[t - 1] * birth_rate
    deaths = population[t - 1] * death_rate
    population[t] = population[t - 1] + births - deaths + annual_net_migration
# 결과 출력
for t in range(years + 1):
    print(f"Year {2023 + t}: {population[t]:,.0f}")

【결과】 Year 2024: 332,155,000 Year 2025: 334,317,542 Year 2026: 336,487,654 Year 2027: 338,665,361 Year 2028: 340,850,689 Year 2029: 343,043,667 Year 2030: 345,244,320 Year 2031: 347,452,675 Year 2032: 349,668,759Year 2033: 351,892,600

8. 전염병 동태

전염 역할 모델른 전염병의 전파와 확산을 연구하는 분야로, 이는 질병의 전염 방식과 전파 속도를 이해하고 예측하는 데 중점을 둔다.

$SIRD$ 모델 상태

$x_{t} = (S,I,R,D),whereS + R + I + D = 1$

감염 가능성 Susceptible (S): 현재는 비감염이지만 내일에는 질병에 감염될 수 있는 사람들
감염 Infected (I): 현재 질병에 감염된 사람들.
회복 Recovered (R): 질병을 회복하고 면역을 획득한 사람들.
사망 Deceased (D): 질병으로 사망한 사람들.

약학 모델 동력학

$\beta$ : 감염 가능성에서 감염으로 전환될 감염율, $\gamma$ : 감염에서 회복으로 전화되는 회복율 $\mu$ : 감염에서 사망으로 전환되는 사망율이라면

\[\begin{matrix} & \frac{dS}{dt} = - \beta SI,\frac{dI}{dt} = - \beta SI - \gamma I\mu I \\ & \frac{dR}{dt} = - \gamma I,\frac{dD}{dt} = \mu I \end{matrix}\]

사례연구

만약 t기의 SIRD 벡터가 $x_{t} = (0.99,0.01,0,0)$라 하자. 그리고 감염 가능성 있는 인구 중 30%($\beta = 0.3$)는 전염되고 전염자의 2%($\mu = 0.02$)는 사망하고 회복율은 10%($\gamma = 0.1)$이라 하자. 그러므로 전염 상태로 남아 있는 전염자는 88%이다.

$x_{t + 1} = Ax_{t}$ 모형에서 $A = \begin{bmatrix} 0.99 & 0.1 & 0 & 0 \\ 0.01 & 0.88 & 0 & 0 \\ 0 & 0.1 & 1 & 0 \\ 0 & 0.02 & 0 & 1 \end{bmatrix}$

# 전염병 동태모델 사례
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# 초기 조건
S0 = 0.99   # 초기 감수성 인구 비율
I0 = 0.01   # 초기 감염 인구 비율
R0 = 0.0    # 초기 회복 인구 비율
D0 = 0.0    # 초기 사망 인구 비율
initial_conditions = [S0, I0, R0, D0]
# 파라미터
beta = 0.3   # 전염율
gamma = 0.1  # 회복율
mu = 0.02    # 사망율
# SIRD 모델 미분 방정식
def sird_model(y, t, beta, gamma, mu):
    S, I, R, D = y
    dS_dt = -beta * S * I
    dI_dt = beta * S * I - gamma * I - mu * I
    dR_dt = gamma * I
    dD_dt = mu * I
    return [dS_dt, dI_dt, dR_dt, dD_dt]
# 시간 벡터 (일 단위)
t = np.linspace(0, 160, 160)
# ODE 풀기
solution = odeint(sird_model, initial_conditions, t, args=(beta, gamma, mu))
S, I, R, D = solution.T
# 결과 그래프 출력
plt.figure(figsize=(10, 6))
plt.plot(t, S, label='Susceptible')
plt.plot(t, I, label='Infected')
plt.plot(t, R, label='Recovered')
plt.plot(t, D, label='Deceased')
plt.xlabel('Time (days)')
plt.ylabel('Proportion of Population')
plt.legend()
plt.title('SIRD Model')
plt.grid(True)
plt.show()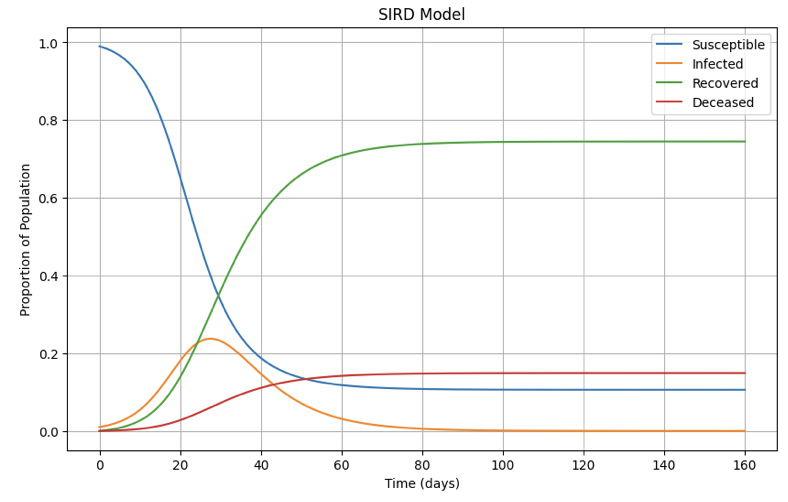

chapter 4. 고유치와 고유벡터

1. 기초

(1) 개념

고유치는 행렬의 선형변환에서 중요한 특성을 나타내는 값이다. 특정 벡터(고유벡터)가 행렬 $A$에 의해 변환될 때, 방향은 변하지 않고 크기만 일정 비율로 변한다면, 이 비율을 고유치라고 한다.

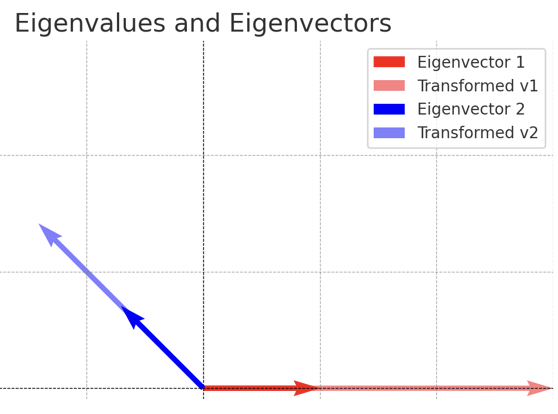
위 그래프는 행렬 $A = \begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix}$의 고유치($\lambda = 3,2$)와 고유벡터의 변환을 시각적으로 보여준다.

빨간색 화살표: 첫 번째 고유벡터 $\mathbf{v}_{1}$
투명 빨간색 화살표: 첫 번째 고유벡터가 행렬 $A$에 의해 변환된 결과로, 고유치 $\lambda_{1} = 3$에 의해 크기만 3배로 늘어난다.
파란색 화살표: 두 번째 고유벡터 $\mathbf{v}_{2}$.
투명 파란색 화살표: 두 번째 고유벡터가 행렬 A 에 의해 변환된 결과로, 고유치 $\lambda_{2} = 2$에 의해 크기만 2배로 늘어난다.

고유벡터의 방향은 행렬 변환 후에도 유지되며, 크기만 고유치 값에 따라 변한다. 이를 통해 고유치와 고유벡터의 개념을 시각적으로 이해할 수 있다.

(2) 통계학 활용

고유치 분석을 통해 얻을 수 있는 통계적 통찰은 다음과 같다.

데이터의 분산 설명: 공분산 행렬의 고유치는 각 축의 분산 크기를 나타내며, 데이터가 어떤 축에서 더 많은 정보를 가지고 있는지 보여준다.
중요한 변수 식별: PCA나 LDA에서 고유치를 사용해 데이터를 가장 잘 설명하는 주성분이나 판별 방향을 찾는다.
데이터의 차원 축소: 가장 큰 고유치를 가진 축만 선택함으로써 데이터의 복잡성을 줄이고, 분석의 효율성을 높는다.
시각화: MDS, PCA를 활용해 고차원 데이터를 저차원으로 투영하여 시각화할 수 있는다.

주성분 분석(PCA, Principal Component Analysis)

PCA는 데이터의 고차원 공간을 낮은 차원으로 축소하면서 데이터의 주요 정보를 보존하는 방법이다.

데이터의 공분산 행렬에서 고유치를 계산하여 주성분의 중요도를 평가한다.
가장 큰 고유치는 데이터의 분산을 가장 많이 설명하는 방향(주성분)을 나타낸다.
예: 변수 100개로 구성된 데이터를 분석할 때, 고유치를 계산하여 주요한 2~3개의 주성분만 선택해 데이터 차원을 축소할 수 있다.

선형 판별 분석(LDA, Linear Discriminant Analysis)

LDA는 여러 클래스 간의 분산을 극대화하면서 각 클래스 내의 분산을 최소화하는 투영 방향을 찾는 방법이다.

클래스 간 분산 행렬과 클래스 내 분산 행렬의 비율로 구성된 행렬의 고유치를 계산하여 최적의 분리 축을 결정한다.

다차원 척도법(MDS, Multidimensional Scaling)

MDS는 데이터 간의 거리 행렬을 기반으로 저차원 공간에 데이터를 시각화하는 방법이다.

거리 행렬을 고유치 분해하여 데이터를 저차원 공간에 배치한다.
가장 큰 고유치를 가진 방향이 데이터 구조의 주요 변화를 설명한다.

공분산 행렬 및 상관 행렬 분석

공분산 행렬이나 상관 행렬의 고유치는 데이터의 선형 독립성과 분산 구조를 분석하는 데 사용된다.

고유치가 큰 방향은 데이터의 분산이 큰 축(정보가 많이 분포된 축)을 나타낸다.
고유치가 0에 가까운 경우 변수들 간의 선형 종속성을 암시한다.

행렬 분해 및 차원 축소

고유치와 고유벡터는 행렬 분해 방법(예: 특이값 분해(SVD), 고유분해(Eigendecomposition))의 핵심이다.

차원 축소, 데이터 압축, 노이즈 제거 등에 사용된다.
예: 특이값 분해(SVD)는 추천 시스템이나 텍스트 분석(Latent Semantic Analysis, LSA)에서 널리 사용된다.

시계열 데이터 분석 Autoregressive 모델(AR)

시계열 모델에서 안정성을 분석할 때, 고유치를 통해 시스템의 특성을 평가한다. 예: 고유치가 1보다 크면 시스템이 불안정함을 나타낸다.

2. 고유치, 고유벡터 구하기

대칭행렬 $A_{n \times n}$에 대하여 고유치 $\lambda$, 고유벡터 $\underset{¯}{v}$는 다음 방정식이 성립한다. $A\underset{¯}{v} = \lambda\underset{¯}{v}$

(1) 고유치 eigenvalue 구하기

$det(A - \lambda I) = 0$을 만족하는 $\lambda$를 고유치라 한다.

고유치는 행렬 $A$의 차수만큼 존재한다. $\lambda_{1},\lambda_{2},...,\lambda_{n}$

(2) 고유벡터 eigenvector 구하기

$A\underset{¯}{v_{i}} = \lambda_{i}\underset{¯}{v_{i}}$ 을 만족하는 벡터($\underset{¯}{v}$)를 고유벡터라 한다.

$det(A - \lambda I) = 0$(singlular)가 성립하므로 고유벡터는 무수히 많이 존재한다.

고유벡터 중 Norm($\underset{¯}{v}'\underset{¯}{v} = 1$)이 1인 고유 벡터를 주성분분석에서 사용한다.

3. 고유치 활용

(1) 고유치 분해 eigenvalue decomposition

정방행렬 $A_{n \times n}A$의 고유치($\lambda_{i}$)를 대각원소로 하는 대각행렬 $\Lambda$, 고유벡터($\underset{¯}{v_{i}}$)로 이루어진 직교 orthogonal 행렬 $Q$라 하면 행렬 $A$는 다음과 같이 고유치 분해 된다. $A = Q\Lambda Q^{- 1}$

(2) 주성분분석

데이터 행렬 : $X_{n \times p} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \cdots & \cdots & \cdots & \cdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}$ (변수 개수 $p$)

$\underset{¯}{y} = P\underset{¯}{x}$ : 원 변수의 선형결합(선형계수 행렬은 고유벡터)으로 주성분변수를 만든다.
$X'X$ 고유치분해 : $X'X = (Q\Lambda Q^{- 1})'(Q\Lambda Q^{- 1}) = Q\Lambda Q^{- 1}$
$X$의 공분산행렬(측정 단위가 다른 경우 상관계수 행렬)로부터 고유치와 고유벡터(Norm=1인 정규고유벡터)를 구하여 서로 독립인 차원으로 변환한다.
공분산행렬에 대한 고유치, 고유벡터 : $COV_{p \times p}\underset{¯}{v} = \lambda\underset{¯}{v}$
공분산 행렬은 양의 정부호 행렬이므로 변수의 차수만큼의 고유치, 그에 대응하는 고유벡터가 존재한다.
고유벡터는 원변수를 직교 축을 갖는 주성분 변수로 변환한다. 그러므로 차수는 줄어들지 않으나 모든 차원에서 관측값은 직교(독립)이다.
주요 2~3개 차원만으로 $p$차원의 원변수 변동(정보)를 축약한다. 이를 주성분분석이라 한다.

(3) 특이값 분해 Singular Value Decomposition

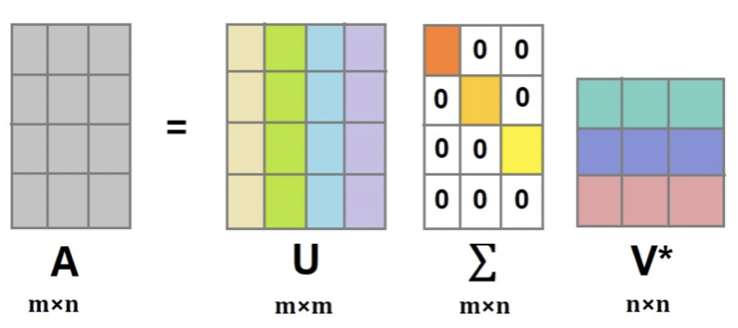
직교행렬 $U$($UU' = I$) : $AA'$의 고유벡터
직교행렬 $V'$($V'V = I$) : $A'A$의 고유벡터
대각행렬 $\Sigma$의 대각원소 : $AA'$, $A'A$의 고유치분해 대각원소의 제곱근 값을 대각원소로 한다.

(4) Cholesky factorization

대칭행렬 $A$가 양의 정부호 행렬일 경우 사용되는 분해방법이다.

$A = LL^{T}$, $L$ : 대각원소가 양이 하단 삼각행렬

【활용】 최소제곱추정과 같은 최적해를 구할 때 사용하면 빠른 연산이 가능하다. $A\underset{¯}{x} = \underset{¯}{b}$ (연립방정식) $\underset{¯}{x} = A^{- 1}\underset{¯}{b}$ ➠ $LL^{T}\underset{¯}{x} = \underset{¯}{b}$ 이것을 풀면 연산이 더 간편하다. $\underset{¯}{x} = (LL^{T})^{- 1}\underset{¯}{b} = (L^{- 1})'L^{- 1}\underset{¯}{b}$

#고유치, 고유벡터
import numpy as np
A=np.array([[1,2,3], [4,5,7],[8,9,10]])
import numpy.linalg as la
val,vec=la.eig(A)
val,vec

【결과】 (array([17.71571559, -1.44163052, -0.27408507]), array([[-0.21078452, -0.49872133, 0.47929184], [-0.52147269, -0.47685414, -0.81047488], [-0.82682291, 0.7238005 , 0.33676373]]))

#고유벡터 분해
import numpy as np
A=np.array([[1,2,3], 
  [4,5,7],
  [8,9,10]])
import numpy.linalg as la
val,vec=la.eig(A)
S=np.diag(val); P=vec
P@S@la.inv(P)

【결과】 array([[ 1., 2., 3.], [ 4., 5., 7.], [ 8., 9., 10.]])

#SVD decomposition
u, s, vh = np.linalg.svd(A, full_matrices=True)
u,s,vh

【결과】 (array([[-0.19462586, -0.6193003 , -0.76064966], [-0.5071685 , -0.6002356 , 0.61846369], [-0.83958376, 0.50614657, -0.19726824]]), array([18.62202941, 1.46779937, 0.25609691]), array([[-0.48007495, -0.56284671, -0.67285334], [ 0.70100172, 0.21497525, -0.67998694], [ 0.52737523, -0.79811604, 0.29135228]]))

#Cholesky decomposition
import numpy as np
A=np.array([[25,15,-5], 
  [15,18,0],
  [-5,0,11]])
import numpy.linalg as la
np.linalg.cholesky(A)

【결과】 array([[ 5., 0., 0.], [ 3., 3., 0.], [-1., 1., 3.]])

#확인 LL'
np.linalg.cholesky(A)@np.linalg.cholesky(A).T

【결과】 array([[25., 15., -5.], [15., 18., 0.], [-5., 0., 11.]])

chapter 5. 행렬미분

1. 미분 공식

(1) 벡터미분

상수벡터 : ${\underset{¯}{a}}_{n} = \left\lbrack \begin{array}{r} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{array} \right\rbrack$ 확률변수 벡터 : ${\underset{¯}{x}}_{n} = \left\lbrack \begin{array}{r} x_{1} \\ x_{2} \\ ... \\ x_{n} \end{array} \right\rbrack$

확률변수 $x_{i} \sim (iid)f(x)$는 확률표본이다.

$\frac{\partial(\underset{¯}{a}'\underset{¯}{x})}{\partial\underset{¯}{x}} = \underset{¯}{a}$, $\frac{\partial(\underset{¯}{x}'\underset{¯}{a})}{\partial\underset{¯}{x}} = \underset{¯}{a}$

(2) 이차형식 미분

$\frac{\partial(\underset{¯}{x}'A\underset{¯}{x})}{\partial\underset{¯}{x}} = (A + A')\underset{¯}{x}$ 만약 A가 대칭행렬이면) $2A\underset{¯}{x}$

2. 이차형식

(1) 이차형식 정의

정방행렬 : $A_{n \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}$

이차형식 : $Q(x_{1},x_{2},...,x_{n}) = \underset{¯}{x}'A\underset{¯}{x}$

2차형식의 경우 대칭행렬인 $A$는 적어도 한 개는 존재한다.

(2) 이차형식 종류

대칭행렬 $A$, 이차형식 $Q(x_{1},x_{2},...,x_{n}) = \underset{¯}{x}'A\underset{¯}{x}$에 대하여

모든 $x \neq 0$에 대하여 $Q > 0$이면 양의 정부호 positive definite

모든 $x \neq 0$에 대하여 $Q \geq 0$이면 양의 반부호 positive semidefinite

(3) 주축정리 The Principal Axes Theorem

이차형식 $\underset{¯}{x}'A\underset{¯}{x}$을 교차항이 없는 이차형식 $\underset{¯}{y}'D\underset{¯}{y}$으로 변환하는 직교변환 $\underset{¯}{x} = P\underset{¯}{y}$ 존재한다. $P$를 주축행렬이라 하고 대칭행렬 $A$의 고유벡터로 이루어져 있다.

교차항이 없는 이차형식은 주축 변량에 대칭이다.

(4) 이차형식과 고유치 관계

이차형식 $Q = \underset{¯}{x}'A\underset{¯}{x}$이 양의 정부호이면 모든 고유치는 0보다 크다.
양의 정부호 행렬의 역행렬도 양의 정부호 행렬이다.
공분산 행렬은 양의 정부호 행렬이다.

3. 이차형식 만들기

\[Q(x) = x_{1}^{2} + 2x_{2}^{2} - 7x_{3}^{2} - 4x_{1}x_{2} + 8x_{1}x_{3}\]

이차형식으로 만들면 다음과 같다. 제곱항은 그대로 대각원소로 하고 교차항은 1/2로 하여 각 셀에 배분한다.

\[Q(x) = \begin{bmatrix} x_{1} & x_{2} & x_{3} \end{bmatrix}\begin{bmatrix} 1 & - 2 & 4 \\ - 2 & 2 & 0 \\ 4 & 0 & - 7 \end{bmatrix}\left\lbrack \begin{array}{r} x_{1} \\ x_{2} \\ x_{3} \end{array} \right\rbrack = \underset{¯}{x}'A\underset{¯}{x}\]

$\underset{¯}{x} = P\underset{¯}{y}$, 주축행렬 $P$는 대칭행렬 $A$의 고유벡터이다.
$A$의 교유치를 대각원소로 하는 행렬 $D = diag(\lambda_{1},\lambda_{2},\lambda_{3})$를 이용하여 교차항이 없는 이차형식으로 변형한다.
이렇게 되면 주축 변환된 이차형식의 변수 간에는 교차항이 없으므로 두 변수간에는 서로 독립이 된다.
$Q(x) = \underset{¯}{x}'A\underset{¯}{x}$ ⇢ $Q(y) = \underset{¯}{y}'D\underset{¯}{y}$ ($\underset{¯}{x} = P\underset{¯}{y}$)

4. 선형 회귀모형

(1) 데이터 구조

목표변수 1개, $p$개 예측변수, 표본크기 n인 데이터를 가정하면 선형 회귀모형은 다음과 같다. $\underset{¯}{y} = X\underset{¯}{\beta} + \underset{¯}{e}$

$\left\lbrack \begin{array}{r} y_{1} \\ y_{2} \\ \cdots \\ y_{n} \end{array} \right\rbrack$=$\begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \cdots & \cdots & \cdots & \cdots & \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}\left\lbrack \begin{array}{r} a \\ b_{1} \\ \cdots \\ b_{p} \end{array} \right\rbrack$+$\left\lbrack \begin{array}{r} e_{1} \\ e_{2} \\ \cdots \\ e_{n} \end{array} \right\rbrack$

(2) 예측변수 데이터 행렬/벡터

$X_{n \times p} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \cdots & \cdots & \cdots & \cdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}$, $X_{n \times p} = \begin{bmatrix} {\underset{¯}{x}}_{1} & {\underset{¯}{x}}_{2} & \cdots & {\underset{¯}{x}}_{p} & \end{bmatrix}$

(데이터 벡터) ${\underset{¯}{x}}_{k} = \left\lbrack \begin{array}{r} x_{1k} \\ x_{2k} \\ \cdots \\ x_{nk} \end{array} \right\rbrack$

(3) 확률변수 벡터, 평균벡터, 공분산행렬

$\underset{¯}{x} = \left\lbrack \begin{array}{r} x_{1} \\ x_{2} \\ \cdots \\ x_{p} \end{array} \right\rbrack$, $x_{i}$는 확률변수이고 $E(x_{i}) = \mu_{i},V(x_{i}) = \sigma_{ii}$,

(두 변수의 공분산) $COV(x_{i},x_{j}) = \sigma_{ij}$

(평균벡터) $E(\underset{¯}{x}) = \underset{¯}{\mu} = \left\lbrack \begin{array}{r} \mu_{1} \\ \mu_{2} \\ \cdots \\ \mu_{p} \end{array} \right\rbrack$

(공분산행렬) $COV(\underset{¯}{x}) = \Sigma = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2p} \\ \cdots & \cdots & \cdots & \cdots \\ \sigma_{p1} & \sigma_{p2} & \cdots & \sigma_{pp} \end{bmatrix}$

상수벡터 : $\underset{¯}{a} = \left\lbrack \begin{array}{r} a_{1},a_{2},\cdots a_{p} \end{array} \right\rbrack$

$\underset{¯}{a}'\underset{¯}{x}$의 평균 : $E(\underset{¯}{a}'\underset{¯}{x}) = \underset{¯}{a}'\underset{¯}{\mu}$, 분산 $V(\underset{¯}{a}'\underset{¯}{x}) = \underset{¯}{a}'\underset{¯}{\Sigma}\underset{¯}{a}$

(4) 선형 회귀모형

$\underset{¯}{y} = X\underset{¯}{b} + \underset{¯}{e}$, $\underset{¯}{e} \sim N(\underset{¯}{0},\sigma^{2}I)$

최소제곱법 추정

\[min_{a,b_{1},b_{2},...,b_{p}}\sum e_{i}^{2} = min_{\underset{¯}{b}}\underset{¯}{e}'\underset{¯}{e}\]

\[Q(\underset{¯}{b}) = \underset{¯}{e}'\underset{¯}{e} = (\underset{¯}{y} - X\underset{¯}{b})'(\underset{¯}{y} - X\underset{¯}{b}) = \underset{¯}{y}'\underset{¯}{y} + \underset{¯}{b}'X'X\underset{¯}{b} - 2\underset{¯}{y}'X\underset{¯}{b}\]

$\frac{\partial Q}{\partial\underset{¯}{b}} = 2X'X\underset{¯}{b} - 2X'\underset{¯}{y} = 0$ ⇢ $\widehat{\underset{¯}{b}} = (X'X)^{- 1}X'\underset{¯}{y}$

적합치 fitted values 와 잔차 residuals

적합치 : $\widehat{\underset{¯}{y}} = X\widehat{\underset{¯}{b}} = X(X'X)^{- 1}X'\underset{¯}{y} = H\underset{¯}{y}$,

$H = X(X'X)^{- 1}X'$ hat 행렬이라 하고 대칭행렬이고 멱등행렬이다. $HH = H,H' = H$

잔차 : $\widehat{\underset{¯}{e}} = \underset{¯}{y} - \widehat{\underset{¯}{y}} = (I - H)\underset{¯}{y}$ $H$가 멱등행렬이면 $(I - H)$도 멱등행렬이다.

잔차의 분포

$\widehat{\underset{¯}{e}} \sim N(\underset{¯}{0},\sigma^{2}I)$

오차의 가정 : $\underset{¯}{e} \sim N(\underset{¯}{0},\sigma^{2}I)$ ⇢ $\underset{¯}{y} \sim N(X\underset{¯}{b},\sigma^{2}I)$

그러므로 $E(\widehat{\underset{¯}{e}}) = (I - H)E(\underset{¯}{y}) = (I - H)(X\underset{¯}{b}) = (X\underset{¯}{b} - HX\underset{¯}{b}) = \underset{¯}{0}V(\widehat{\underset{¯}{e}}) = V((I - H)\underset{¯}{y}) = (I - H)\sigma^{2}I(I - H)' = \sigma^{2}I$

목표변수 분해

$\underset{¯}{y} = H\underset{¯}{y} + (I - H)\underset{¯}{y}$=(설명하는 변동) + (설명하지 못하는 변동)

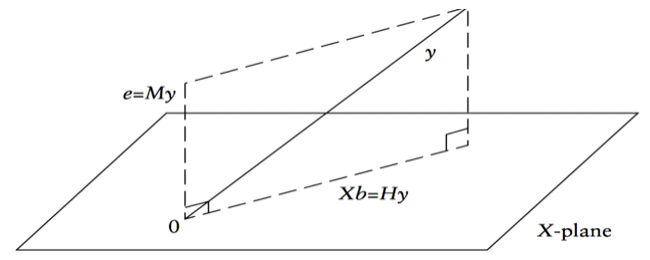
높이를 최소화 하는 $\underset{¯}{b}$를 구하는 것이 최소제곱추정법이다.

추정치 분포

$\widehat{\underset{¯}{b}} = (X'X)^{- 1}X'\underset{¯}{y}$이고 $\underset{¯}{y} \sim N(X\underset{¯}{b},\sigma^{2}I)$이므로

\[E(\widehat{\underset{¯}{b}}) = (X'X)^{- 1}X'E(\underset{¯}{y}) = (X'X)^{- 1}X'X\underset{¯}{b} = \underset{¯}{b}\]

\[V(\widehat{\underset{¯}{b}}) = \sigma^{2}(X'X)^{- 1}\]

$\widehat{\underset{¯}{b}} \sim N(\underset{¯}{b},\sigma^{2}(X'X)^{- 1})$, ${\widehat{\sigma}}^{2} = SSE$

변동 분해 ANOVA

총변동 Total Sum of Squares : $SST = \sum(y_{i} - \overline{y})^{2}$

$SST = \sum y_{i}^{2} - \frac{(\sum y_{i})^{2}}{n} = \underset{¯}{y}'\underset{¯}{y} - (\frac{1}{n})\underset{¯}{y}'J_{n \times n}\underset{¯}{y}$, $J$는 1행렬

\[SST = \underset{¯}{y}'(I - (\frac{1}{n})J)\underset{¯}{y}\]

오차변동 Error Sum of Squares

\[SSE = \sum(y_{i} - \widehat{y_{i}})^{2}\]

\[SSE = (\underset{¯}{y} - X\underset{¯}{b})'(\underset{¯}{y} - X\underset{¯}{b}) = \underset{¯}{y}'\underset{¯}{y} - \underset{¯}{b}'X'\underset{¯}{y} = \underset{¯}{y}'(I - H)\underset{¯}{y}\]

회귀변동 Regression Sum of Squares

$SSR = \sum(\widehat{y_{i}} - \overline{y})^{2}$, $SSR = \underset{¯}{y}'(H - (\frac{1}{n})J)\underset{¯}{y}$

\[SSR = SST - SSE = \underset{¯}{b}X'\underset{¯}{y} - (\frac{1}{n})\underset{¯}{y}'J\underset{¯}{y}\]

결정계수

$R^{2} = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$ : 모형의 총변동 설명 비중

SSE, SSR 분포 및 $\sigma^{2}$ 추정량

$\underset{¯}{x} \sim N(\underset{¯}{\mu},\Sigma)$ 이면 이차형식 $\underset{¯}{x}'A\underset{¯}{x}$의 평균은
$E(\underset{¯}{x}'A\underset{¯}{x}) = tr(A\Sigma) + \mu'A\mu$이다.

$\underset{¯}{x} \sim N(\underset{¯}{\mu},\sigma^{2}I)$ 이면 이차형식 $\underset{¯}{x}'A\underset{¯}{x}$($A$ 대칭행렬이고 멱등행렬이면)에 대하여 $\frac{\underset{¯}{x}'A\underset{¯}{x}}{\sigma^{2}} \sim \chi^{2}(df = rank(A))$이다.

$SSE = \underset{¯}{y}'(I - H)\underset{¯}{y}$, 이차형식이고 $(I - H)$는 멱등행렬
$rank(I - H) = n - p - 1$이므로 $\frac{SSE}{\sigma^{2}} \sim \chi^{2}(n - p - 1)$이다.

오차 분산의 추정량 : $\widehat{\sigma^{2}} = MSE$.

$\frac{SSR}{\sigma^{2}} \sim \chi^{2}(p)$, $F = \frac{SSR/p}{SSE/(n - p - 1)} \sim F(p,n - p - 1)$

분산분석 표

변동	제곱변동	자유도	평균제곱	F
회귀	\[SSR\]	\[p\]	\[MSR = \frac{SSR}{p}\]	\[\frac{MSR}{MSE}\]
오차	\[SSE\]	\[n - p - 1\]	\[MSE = \frac{SSE}{n - p - 1}\]	\[\frac{MSR}{MSE}\]
총변동	\[SST\]	\[n - 1\]	\[{E(MSE) = \sigma^{2} }{E(MSR) = \sigma^{2} + b_{1}^{2}\sum(x_{i} - \overline{x})^{2}}\]

%% 강제 리렌더용 주석

역행렬 \(A^{- 1}\)은 존재한다.	역행렬 \(A^{- 1}\)은 존재하지 않는다.
행렬식은 0이 아니다. \(det(A) \neq 0\)	행렬식은 0이다. \(det(A) = 0\)
full rank이다. \(rank(A) = n\)	full rank 아니다. \(rank(A) < n\)
행렬 A는 non-singular이다.	행렬 A는 singular이다.
\(AX = \underset{¯}{b}\) 해가 존재한다.	\(AX = \underset{¯}{b}\) 해가 존재하지 않는다.