MLDL 딥러닝 분류
Chapter 딥러닝 분류
딥러닝 분류는 입력 \(x \in \mathbb{R}^{d}\)가 주어졌을 때, 출력 y가 어떤 클래스에 속하는지 예측하는 문제이다. 전통적 분류(로지스틱 회귀, LDA 등)가 비교적 명시적 확률모형 혹은 선형 결정규칙을 강조했다면, 딥러닝 분류는 표현학습을 통해 복잡한 비선형 결정경계를 자동으로 학습한다는 점이 핵심이다.
딥러닝 분류를 이해할 때는 ”모형이 무엇을 내놓고(출력층), 그 출력을 어떻게 확률로 바꾸며, 어떤 손실을 최소화하는가”를 한 덩어리로 보는 것이 중요하다. 특히 분류에서 실무적 의사결정은 다음의 3단계를 분리해서 생각하면 정리된다.
아직 확률이 아니라, 클래스별로 얼마나 그럴듯한지를 나타내는 원시적인 척도이며 보통 \(logitz = (z_{1},\ldots,z_{K})\) 형태로 출력된다.
다음으로 이 점수 벡터를 확률로 해석할 수 있도록 변환한다. 다중분류라면 점수들 사이의 상대적 크기를 반영해 합이 1이 되도록 만드는 softmax를 적용하고, 이진분류나 멀티라벨이라면 각 클래스의 ”존재 확률”을 독립적으로 해석하기 위해 sigmoid를 적용해 p를 얻는다.
마지막으로 이렇게 얻어진 확률 p를 실제 의사결정으로 연결한다. 다중분류에서는 가장 큰 확률을 가진 클래스를 선택하여 \(\widehat{y} = \arg\max_{k}p_{k}\)로 예측하고, 이진/멀티라벨에서는 특정 임계값 t를 기준으로 \(p \geq t\)이면 양성, 그렇지 않으면 음성으로 판정한다. 즉 딥러닝 분류는 ”점수를 계산하고 → 확률로 바꾸고 → 운영 규칙에 따라 결정한다”는 흐름으로 정리할 수 있다.
0. 개요: 딥러닝 분류는 무엇을 학습하나?
딥러닝 분류는 입력 데이터로부터 각 클래스(또는 라벨)에 대한 점수를 만들고, 그 점수를 확률로 변환한 뒤, 운영 목적에 맞는 결정 규칙을 적용해 행동으로 연결하는 학습 과정이다. 핵심은 단순히 ”정답을 맞히는 것”에 그치지 않고, 얼마나 확신하는지(확률의 품질) 까지 포함하여 모델을 설계·학습·평가한다는 점이다. 즉 분류는 ”모델 출력 → 확률 → 임계값/정책”이 이어지는 전체 파이프라인 문제로 이해하는 것이 중요하다.
분류 문제와 목표: 점수–확률–결정
신경망 분류기는 보통 마지막 층에서 클래스별로 점수(로짓/스코어) 를 출력한다. 이 점수는 ”확률”이 아니라, 모델이 각 클래스에 대해 얼마나 강하게 판단하는지를 나타내는 내부 지표에 가깝다.
운영에서 바로 활용하려면, 점수를 사람이 해석 가능한 형태인 확률로 바꾸는 변환이 필요하다. 이 변환 방식은 문제의 라벨 구조에 따라 달라진다(이진, 다중 단일정답, 멀티라벨 등).
마지막으로 실제 의사결정은 확률을 그대로 쓰기보다, 임계값(threshold) 이나 규칙(rule) 을 적용해 ”양성/음성”, ”어느 클래스”, ”검토로 넘김” 같은 행동으로 변환한다. 여기서 중요한 점은, 학습이 추구하는 목표(손실 최소화)와 운영이 요구하는 목표(오경보/미탐 비용, 검토량 제한, 위험 기준 등)가 항상 동일하지 않다는 것이다. 따라서 분류 성능은 ”학습 단계”뿐 아니라 ”운영 단계의 결정 규칙”까지 포함해 설계해야 한다.
데이터/라벨 구조: 이진, 다중(단일정답), 멀티라벨
딥러닝 분류에서 가장 먼저 확인해야 할 것은 라벨 구조다. 라벨 구조가 달라지면 출력층 형태, 확률 변환 방식, 손실 함수, 평가 지표가 함께 달라진다.
이진 분류는 한 관측치가 두 범주 중 하나에 속하는 문제다. 모델은 ”양성일 가능성” 하나를 중심으로 점수와 확률을 설계한다.
다중 분류(단일 정답) 는 여러 클래스 중 하나만 정답인 문제다. 모델은 여러 클래스 점수를 동시에 만들고, 그중 하나를 선택하는 구조로 설계한다.
멀티라벨 분류는 한 관측치가 여러 라벨을 동시에 가질 수 있는 문제다. 각 라벨을 ”독립적인 예/아니오” 문제처럼 다루는 방식이 일반적이며, 따라서 출력과 확률도 라벨별로 따로 해석한다.
이 구분은 단순한 형식 차이가 아니라, ”모델이 무엇을 맞히도록 학습되는가”와 ”운영에서 무엇을 결정해야 하는가”를 바꾸는 근본 요소다.
손실 함수의 역할: 확률을 ’학습 목표’로 만드는
장치
손실 함수는 모델이 출력한 확률이 정답 라벨과 일치하도록 학습을 유도하는 장치다. 직관적으로 말하면, 정답에 높은 확률을 주면 보상, 오답에 높은 확률을 주면 페널티를 주는 방식으로 작동한다.
다만 손실 함수는 단지 ”정확도”만을 직접 최적화하는 것이 아니라, 예측의 확신 정도까지 반영한다. 그래서 같은 정확도라도 확률이 지나치게 과감하거나(과신) 너무 소극적인 모델은 운영에서 문제가 될 수 있다.
또한 멀티라벨처럼 라벨 구조가 바뀌면 손실의 형태도 달라지며, 불균형 데이터처럼 특정 오류가 더 치명적인 상황에서는 손실을 조정해 학습의 초점을 바꾸기도 한다(이 내용은 이후 절에서 상세히 다룬다).
학습과 일반화: ”훈련 성능”이 아니라 ”새 데이터
성능”이 목표
딥러닝 분류의 성능은 훈련 데이터에서의 성능이 아니라, 보지 못한 새 데이터에서의 성능, 즉 일반화 성능으로 평가된다. 신경망은 표현력이 매우 커서 훈련 데이터를 거의 외워버릴 수도 있기 때문에, 훈련 성능이 좋아지는 것이 곧바로 실제 성능 개선을 의미하지는 않는다.
과적합이 나타나면 흔히 다음과 같은 현상이 함께 관찰된다.
훈련에서는 계속 좋아지는데, 검증/테스트에서는 어느 순간부터 성능이 정체되거나 나빠진다.
예측 확률이 0 또는 1 같은 극단으로 치우치며, 모델이 지나치게 확신하는 경향(과신)이 동반된다.
따라서 분류 모델은 ”학습”과 함께 ”일반화”를 동시에 설계해야 한다.
일반화를 좌우하는 실무 레버: 정규화와 학습 안정화
일반화를 개선하는 대표적 방법들은 크게 두 부류로 정리할 수 있다.
- 정규화(Regularization): 모델이 훈련 데이터에 과도하게 맞춰지는 것을 억제해 일반화를 돕는 장치들이다. 대표적으로 가중치 규제, 드롭아웃, 조기 종료(early stopping) 등이 있으며, 경우에 따라 확률의 과신을 완화하는 데에도 도움이 된다.
- 학습 안정화(Stabilization): 학습 자체가 불안정해 성능이 흔들리는 문제를 줄이는 기법들이다. 최적화가 안정되면 일반화도 함께 좋아지는 경우가 많으며, 배치정규화 같은 기법이 대표적이다.
데이터 규모와 모델 규모의 균형: 작은 데이터일수록 전략이 달라진다
실무에서 가장 중요한 감각 중 하나는 데이터 규모와 모델 규모의 균형이다.
- 데이터가 작을수록, 큰 모델을 그대로 쓰기보다 모델을 단순화하거나 정규화를 강하게 하고, 사전학습 모델을 활용하는 전략의 가치가 커진다.
- 데이터가 충분히 클수록, 모델 규모를 키워 표현력을 확보할 수 있고, 증강이나 정규화는 ”성능 극대화”보다 ”학습 안정성 확보” 용도로 조절되는 경우가 많다.
즉, 같은 분류 문제라도 데이터 환경에 따라 ”어떤 방법론을 우선 적용할지”가 달라진다.
1. 출력 설계(라벨 구조에 따른 분류 정식화)
딥러닝 분류에서 출력층(output layer) 은 ”마지막 층” 이상의 의미를 가진다. 신경망이 만든 점수(score, logit) 를 확률(probability) 로 변환하여 해석 가능하게 만들고, 그 확률을 바탕으로 운영 단계의 결정(decision) 규칙(임계값, Top-k, 비용민감 규칙 등)이 적용될 수 있도록 확률모형의 형태 자체를 결정한다.
따라서 출력 설계는 ”모델이 무엇을 학습하느냐”와 동시에 ”운영에서 무엇을 결정할 수 있느냐”를 규정하며, 라벨 구조(이진/다중 단일정답/멀티라벨)를 먼저 확정하지 않으면 손실함수·평가·의사결정 규칙이 서로 충돌해 학습이 불안정해질 수 있다.
(1) 점수(score) → 확률(probability) → 결정(decision)
분류 모델의 흐름은 보통 다음 3단계로 이해하는 것이 가장 안전하다.
1. 점수(score): 신경망 f_\theta가 입력 x로부터 계산한 값
2. 확률(probability): 점수를 확률로 변환(라벨 구조에 따라 변환이 달라짐)
3. 결정(decision): 확률에 임계값/정책/Top-k 규칙을 적용하여 최종 예측 또는 행동을 결정
점수는 임의의 실수이고(확률이 아님), 확률은 운영에서 해석 가능한 형태이며, 결정은 ”정답 맞추기”가 아니라 비용, 제약, 서비스 목표를 반영하는 규칙이다. 이 장은 2)까지(확률모형 설계)를 중심으로 정리하되, 3)과의 연결고리(임계값/Top-k/비용민감)를 함께 제시한다.
(2) 이진 분류: logit 1개와 sigmoid 확률모형
이진 분류는 라벨이 \(Y \in \{ 0,1\}\)인 문제다. 신경망은 마지막에서 단일 점수를 출력한다. \(z = f_{\theta}(x) \in \mathbb{R}\)
이 점수 z는 ”양성일수록 크게” 학습되는 방향으로 해석하면 된다. 확률모형은 이 점수를 sigmoid로 변환하여 \(p(x) = P(Y = 1 \mid X = x) = \sigma(z) = \frac{1}{1 + e^{- z}}\)로 정의한다. 그러면 \(P(Y = 0 \mid x) = 1 - p(x)\)가 자동으로 결정된다.
logit과 log-odds 해석(확률모형 관점)
sigmoid는 다음 관계를 만족한다.
\[\frac{p(x)}{1 - p(x)} = e^{z},\log\frac{p(x)}{1 - p(x)} = z\]
즉 z는 조건부 확률의 로그 오즈(log-odds) 로 해석된다. 이 관점은 딥러닝 이진분류가 ”확률을 직접 출력한다”기보다, 먼저 log-odds를 예측하고 이를 확률로 변환하는 구조임을 분명히 해 준다.
(3) 다중 분류(단일정답): 클래스별 logit과 softmax 확률모형
다중 분류(멀티클래스, 단일 정답)는 라벨이 \(Y \in \{ 1,\ldots,K\}\)이고, 각 관측치의 정답이 정확히 하나인 경우다. 신경망은 클래스별 점수 벡터를 출력한다. \(\mathbf{z} = f_{\theta}(x) = (z_{1},\ldots,z_{K}) \in \mathbb{R}^{K}\)
이를 확률 벡터로 바꾸는 표준 변환이 softmax이다.
\[p_{k}(x) = P(Y = k \mid X = x) = \frac{e^{z_{k}}}{\sum_{j = 1}^{K}e^{z_{j}}},k = 1,\ldots,K\]
softmax의 핵심은 \(p_{k}(x) \in (0,1)\), \(\overset{K}{\sum_{k = 1}}p_{k}(x) = 1\)을 만족한다는 점이며, 이는 ”확률 질량을 K개 클래스에 분배”하는 구조를 의미한다. 따라서 단일정답 다중 분류에서는 클래스들이 서로 경쟁한다.
softmax 불변성(수치안정성의 핵심)
모든 logit에 같은 상수 c를 더해도 확률은 변하지 않는다.
\(\frac{e^{z_{k} + c}}{\sum_{j}^{}e^{z_{j} + c}} = \frac{e^{z_{k}}}{\sum_{j}^{}e^{z_{j}}}\). 이 성질 때문에 실제 구현에서는 overflow 방지를 위해 보통 \(p_{k} = \frac{e^{z_{k} - \max_{j}z_{j}}}{\sum_{j}^{}e^{z_{j} - \max_{j}z_{j}}}\)처럼 최대값을 빼서 계산한다.
(4) 결정 규칙: MAP 규칙과 비용민감(cost-sensitive) 일반화
확률모형이 정해지면, 최종 예측은 결정 규칙으로 나온다. 가장 기본 규칙은 최대확률(MAP) 규칙이다.
\[\widehat{y}(x) = \arg\max_{k}p_{k}(x)\]
softmax는 단조 변환 구조이므로 \(\arg\max_{k}p_{k}(x) = \arg\max_{k}z_{k}\)도 성립한다. 하지만 현실에서는 오분류 비용이 클래스별로 다를 수 있다. 행동 a를 취했을 때의 비용을 C(a,k)로 두면, 최적 결정은 기대비용을 최소화하는 규칙이 된다.
\[\widehat{a}(x) = \arg\min_{a}\overset{K}{\sum_{k = 1}}C(a,k)p_{k}(x)\]
MAP 규칙은 ”모든 오분류 비용이 동일”한 특수한 경우로 볼 수 있다. 이 점 때문에 운영에서는 단순 정확도보다 임계값/정책 설계가 중요해진다.
(5) 멀티클래스 vs 멀티라벨: 출력 구조가 달라지는 이유
이름이 비슷해 혼동이 잦지만, 두 문제는 라벨 의미가 다르다.
- 멀티클래스(단일정답): ”K개 중 정확히 하나” \(\Rightarrow softmax,\sum_{k}p_{k} = 1\)
- 멀티라벨: ”K개 라벨이 각각 존재/부재(여러 개 동시 가능)” → 라벨별 sigmoid, 라벨 간 경쟁 제약 없음
멀티라벨의 라벨 벡터는 보통 \(\mathbf{Y} = (Y_{1},\ldots,Y_{K}) \in \{ 0,1\}^{K}\)로 표현하며 목표는 각 라벨의 조건부 확률 \(p_{k}(x) = P(Y_{k} = 1 \mid X = x)\)를 추정하는 것이다.
(6) 멀티라벨 출력층: 라벨별 sigmoid + (독립) BCE 합
멀티라벨 신경망은 마지막에 K개의 logit을 출력한다.
\[\mathbf{z} = f_{\theta}(x) = (z_{1},\ldots,z_{K}) \in \mathbb{R}^{K}\]
각 logit을 라벨별 sigmoid로 변환해 라벨별 확률을 만든다.
\[p_{k}(x) = \sigma(z_{k}),k = 1,\ldots,K\]
그리고 표준 손실은 라벨별 이진 교차엔트로피(BCE)를 합한 형태다.
\[\mathcal{L}_{ML}(y,p) = - \overset{K}{\sum_{k = 1}}\left( y_{k}\log p_{k} + (1 - y_{k})\log(1 - p_{k}) \right)\]
이 구성은 ”각 라벨이 독립적인 베르누이 타깃”이라는 모델링 관점과 대응한다.
현실에서는 라벨 간 상관이 존재할 수 있지만, 예측은 라벨별 확률로 두고(독립 형태), 공유 표현(shared representation) 을 통해 상관을 간접적으로 흡수하는 방식이 실무적으로 널리 쓰인다.
(7) ”멀티라벨에 softmax를 쓰면 왜 문제인가?”
softmax는 \(\sum_{k}p_{k} = 1\) 을 강제한다. 즉 라벨들이 확률 질량을 나눠 갖는 경쟁 구조가 된다.
하지만 멀티라벨은 ”사람”과 ”자전거”가 동시에 존재할 수 있어 둘 다 높은 확률이어야 자연스럽다. softmax는 둘 다 0.9처럼 동시에 크게 만드는 것을 구조적으로 허용하지 않는다(한쪽이 커지면 다른 쪽은 상대적으로 줄어듦).
따라서 라벨이 비배타적일 가능성이 있다면, 출력층은 멀티라벨 설계(라벨별 sigmoid)로 가야 한다.
(8) 멀티라벨의 임계값 전략: global vs 라벨별 \(t_k\)
멀티라벨의 최종 예측은 라벨별 임계값을 적용해 이진화한다. \({\widehat{y}}_{k} = \mathbf{1}(p_{k} \geq t_{k})\) 여기서 임계값 설정이 성능과 운영량을 크게 좌우한다. 대표 전략은 두 가지다.
(A) Global threshold: 전 라벨 공통 임계값 \(t_{k} = t,\forall k\)
단순하고 운영/설명이 쉽고, 튜닝 비용 낮은 장점이 있느나, 라벨별 빈도(희귀도), 비용, 난이도가 다르면 비효율적이라는 단점이 있다. (희귀 라벨은 보통 더 낮은 임계값이 필요하지만 공통 임계값은 이를 반영하기 어렵다)
(B) 라벨별 threshold: \(t_{1},\ldots,t_{K}\) 개별 튜닝
라벨별 불균형/비용/난이도를 반영 가능 → 실무 성능 향상 가능성이 크다는 장점이 있으나 관리 복잡도 증가(라벨 수가 많을수록), 데이터가 적으면 과적합 위험이 발생한다.
실무에서는 검증셋에서 라벨별 기준을 정해 \(t_{k}\)를 선택한다. 예컨대 라벨별 F1 최대화 기준, 라벨별 FPR 제약(알람 오경보 제한), 라벨별 운영량(일일 알람 수 상한) 기반 등으로 결정한다.
(9) 멀티라벨 평가 요약: micro vs macro, PR 관점
멀티라벨에서는 ”정확도(accuracy)“가 의미가 약해지는 경우가 많아, 보통 Precision/Recall/F1을 micro/macro로 요약한다.
Micro 평균: 전체 라벨·전체 샘플의 TP/FP/FN을 한데 모아 계산
\[\begin{matrix} TP_{\text{micro}} & = \sum_{k}TP_{k}, \\ FP_{\text{micro}} & = \sum_{k}FP_{k}, \\ FN_{\text{micro}} & = \sum_{k}FN_{k}, \\ {Precision}_{\text{micro}} & = \frac{TP_{\text{micro}}}{TP_{\text{micro}} + FP_{\text{micro}}}, \\ {Recall}_{\text{micro}} & = \frac{TP_{\text{micro}}}{TP_{\text{micro}} + FN_{\text{micro}}}, \\ F1_{\text{micro}} & = \frac{2{Precision}_{\text{micro}}{Recall}_{\text{micro}}}{{Precision}_{\text{micro}} + {Recall}_{\text{micro}}}. \end{matrix}\]
→ 자주 등장하는(빈도 큰) 라벨이 지표에 더 큰 영향
Macro 평균: 라벨별 점수를 평균
\[\begin{array}{r} Precision_{\text{macro}} = \frac{1}{K}\overset{K}{\sum_{k = 1}}Precision_{k}, \\ Recall_{\text{macro}} = \frac{1}{K}\overset{K}{\sum_{k = 1}}Recall_{k}, \\ F1_{\text{macro}} = \frac{1}{K}\overset{K}{\sum_{k = 1}}F1_{k} \end{array}\]
→ 희귀 라벨도 동일 가중치로 반영(”모든 라벨을 고르게 잘하나?“)
또한 멀티라벨은 라벨별 양성 비율이 크게 다르므로 ROC보다 PR(Precision–Recall) 곡선이 더 직접적인 경우가 많다. 운영에서는 ”Recall을 조금 올리려다 FP가 폭증하는 구간”이 흔하므로, PR 곡선으로 임계값 민감도를 확인하는 것이 중요하다.
(10) Large-K(대규모 클래스) 분류: softmax가 학습/추론 병목이 되는 경우
클래스 수 K가 수만~수백만으로 커지는 문제(상품/문서/광고 ID 예측, 추천, 검색 쿼리–문서 매칭 등)에서는 ”모델이 무엇을 학습하느냐”보다 softmax를 어떻게 계산하느냐가 학습·추론의 병목이 된다. 핵심은 한 번의 학습 스텝에서 필요한 계산이 기본적으로 O(K) 로 커지기 때문이다.
softmax 계산 병목과 메모리 이슈
다중분류에서 \(logit\mathbf{z} \in \mathbb{R}^{K}\)에 대해 \(p_{k} = \frac{e^{z_{k}}}{\sum_{j = 1}^{K}e^{z_{j}}}\)를 계산하려면 분모 \(\sum_{j = 1}^{K}e^{z_{j}}\)가 필요하므로 모든 클래스 logit을 한 번은 계산해야 한다. 병목은 크게 두 가지다.
(A) 시간 복잡도: O(K) softmax + loss
정답이 y일 때 cross-entropy는 \(\mathcal{L} = - \log p_{y} = - z_{y} + \log\overset{K}{\sum_{j = 1}}e^{z_{j}}\)이므로 \(\log\sum_{j}e^{z_{j}}\) 계산이 핵심 비용이다. K가 커지면 한 배치에서 이 항을 계산하는 비용이 지배적이 된다.
(B) 출력층 파라미터 메모리: O(Kd)
마지막 선형층이 보통 \(z_{k} = \mathbf{w}_{k}^{\top}\mathbf{h} + b_{k},\mathbf{h} \in \mathbb{R}^{d}\) 형태이므로 출력층 가중치 \(W \in \mathbb{R}^{K \times d}\)를 저장해야 한다. 파라미터 수는 Kd (+ bias K)로 증가한다. K가 수백만이면 이 층만으로도 GPU 메모리 한계에 부딪히며, 분산 학습/샤딩이 필요해진다.
Sampled softmax: ”분모를 일부 클래스만으로 근사”
Large-K의 대표 아이디어는 ”정답 클래스 1개 + 일부 음성 클래스”만 사용해 학습 신호를 만들고, 전체 K에 대한 softmax 계산을 피하는 것이다.
샘플마다 정답 y와 음성 샘플 집합 \(S \subset \{ 1,\ldots,K\} \smallsetminus \{ y\},|S| = m \ll K\)를 뽑아 ”부분 softmax”로 근사한다.
개념적으로는 \(\log\overset{K}{\sum_{j = 1}}e^{z_{j}} \approx \log(e^{z_{y}} + \sum_{j \in S}e^{z_{j}})\)를 사용한다. 실제로는 샘플링 분포에 따른 보정항을 넣어 편향을 줄이는 변형이 많다.
학습 시 클래스 연산이 K에서 m으로 줄어들어 비용이 O(m)이 되지만, 근사이므로 샘플링 전략과 보정 방식이 품질을 좌우한다.
Negative sampling: ”분류”를 ”정답 vs 음성”의 랭킹 학습으로
negative sampling은 softmax의 분모를 근사한다기보다, 관점을 바꿔 ”정답 쌍”과 ”음성 쌍”을 구분하도록 학습하는 성격이 강하다. 점수 \(s(x,k)\)를 사용해 정답 쌍 \((x,y)\)는 양성, 샘플된 음성 \((x,j)\)는 음성으로 두고 \(\mathcal{L} = - \log\sigma(s(x,y)) - \sum_{j \in S}\log\sigma( - s(x,j))\) 같은 형태의 손실로 학습한다. 직관은 단순하다. 정답의 점수는 크게하고 음성의 점수는 작게한다.
특히 추천/검색처럼 ”확률의 정규화”보다 Top-k 랭킹 품질이 핵심인 문제에서 negative sampling은 자주 쓰인다.
샘플링의 핵심: 음성을 어떻게 뽑을 것인가?
무작위 음성은 너무 쉬워 학습 신호가 약할 수 있다. 그래서 자주 쓰는 전략이 빈도 기반 샘플링(자주 나오는 클래스에 더 많이), hard negative(현재 모델이 헷갈리는 클래스), in-batch negative(같은 배치의 다른 정답들을 음성으로 활용) 등이다. Large-K에서 성능 차이는 종종 ”모델 구조”보다 ”negative 구성”에서 크게 난다.
Retrieval + Rerank(2-stage): 분류를 ”찾기(search)” 문제로 재정의
Large-K 문제를 ”분류”로만 보면 softmax가 병목이지만, 관점을 바꾸면 본질은 종종 Top-N 후보를 잘 찾는 문제다. 즉 전체 K 중 ”상위 몇 개”만 정확하면 되는 경우가 많다. 이때 표준 해법이 2-stage 구조다.
Stage 1: Retrieval(후보 생성)
입력 x를 임베딩 \(\mathbf{h}(x) \in \mathbb{R}^{d}\)로 만들고, 클래스(또는 아이템)도 임베딩 \(\mathbf{e}_{k} \in \mathbb{R}^{d}\)로 두어 유사도로 후보를 찾는다. \(score(x,k) = \mathbf{h}(x)^{\top}\mathbf{e}_{k}\)
그리고 ANN(Approximate Nearest Neighbor) 같은 근사 최근접 탐색으로 Top-N 후보를 빠르게 가져온다. 이 단계의 목적은 ”정확도”보다 회수(recall), 즉 정답 후보를 넓게 포함하는 것이다.
Stage 2: Rerank(정밀 재정렬)
1단계 후보 N개(예: 100~1000개)만 놓고, 더 무거운 모델(딥 네트워크, cross-attention 등)로 정교하게 점수화해 최종 Top-k를 결정한다.
\[\widehat{y} \in \text{Top-}k\text{of}\{ rerank\_ score(x,c):c \in \mathcal{C}_{N}\}\]
왜 2-stage가 강력한가? 전체 K에 대해 매번 계산하지 않아도 되어 추론 비용이 크게 감소하고 목표가 ”정규화된 확률”이 아니라 랭킹/Top-k 품질일 때 자연스럽게 맞을 뿐 아니라 검색/추천의 운영 요구(지연시간 제한, Top-k 응답)에 잘 부합한가.
Large-K에서는 ”확률의 정확한 정규화”보다 ”상위 후보를 얼마나 잘/빠르게 찾는가”가 더 중요해져, 분류가 검색(retrieval) 문제로 재정식화되는 경우가 많다.
무엇을 언제 쓰나? (Large-K 의사결정 가이드)
Large-K에서 핵심 선택지는 ”끝까지 분류(softmax 계열)로 갈 것인가” vs ”문제를 검색/랭킹으로 재정식화할 것인가”다.
Sampled softmax / negative sampling을 우선 고려하는 경우
(A) 목표가 정규화된 확률에 가깝다: 다음 토큰 확률(언어모델), 확률 자체가 다운스트림에 직접 쓰이는 경우 → softmax는 \(\sum_k p_k=1\) 인 분포를 제공하므로 확률 해석이 필요할 때 유리
(B) 학습은 대규모지만 서빙은 상대적으로 단순/오프라인: 학습에서 샘플링으로 가볍게 만들고, 추론은 필요한 범위에서 계산하는 절충 가능
(C) 라벨이 명확한 1-of-K closed-set 구조: 카테고리/클래스가 고정되고 정답이 하나인 폐집합 분류는 CE 프레임을 유지하는 것이 자연스럽다.
(D) 평가/목표가 Top-1 정확도 중심: CE 기반 학습은 top-1 분류 성격과 결이 잘 맞는다.
Retrieval + Rerank(2-stage)를 우선 고려하는 경우
(A) 목표가 Top-k 추천/검색이며 전체 확률이 필요 없다.: ”상위 10개/50개를 잘 맞추기”가 목표면 2-stage가 자연스럽다.
(B) 초저지연/대규모 서빙이 필수: 온라인 추천/검색에서 ms 단위 지연 제한이면 전체 K 스코어링은 사실상 불가능에 가깝고, ANN 기반 retrieval이 정답에 가깝다.
(C) 클래스/아이템이 자주 추가·삭제되는 동적 카탈로그: 분류 출력층 테이블(K\times d)을 계속 재학습·동기화하기 어렵다. 임베딩 인덱스 기반 retrieval은 추가/갱신이 비교적 수월하다.
(D) 랭킹 지표(NDCG, MAP, Recall@k)가 중요하고 hard negative를 잘 만들고 싶다.: 2-stage는 1단계가 회수(recall), 2단계가 정밀도(precision)를 담당해 랭킹 최적화에 유리하다.
확률이 꼭 필요하면 sampled softmax(또는 계층 softmax 등) 쪽으로 Top-k 품질이 핵심이면 negative sampling / retrieval+r erank 쪽으로 기운다.
최종 체크리스트(출력 설계)
1. 출력이 ”확률분포(\sum_k p_k=1)“로 꼭 필요한가? → Yes: softmax 계열(필요 시 sampled/근사) / No: retrieval+rerank 또는 negative sampling
2. 라벨이 단일정답인가, 멀티라벨인가? → 단일정답: softmax / 멀티라벨: 라벨별 sigmoid
3. K가 매우 큰가(수만~수백만)? → Yes: 근사 softmax, negative sampling, 2-stage 중 운영 목표에 맞게 선택
4. 운영 목표가 accuracy인가, Recall@k/NDCG/MAP인가? → accuracy: CE/softmax 프레임 선호 → 랭킹 지표: negative sampling + 2-stage 설계가 자연스럽다
2. 손실 함수와 학습 목적 (Loss & Objective)
딥러닝 분류에서 손실함수(loss)는 ”정답을 맞추라”는 막연한 지시가 아니라, 확률모형 \(P_{\theta}(Y \mid X)\)가 데이터에 맞게 추정되도록 만드는 통계적 기준이다. 분류에서 가장 표준적인 손실은 Cross-Entropy(교차엔트로피) 이며, 이는 곧 음의 로그우도(NLL, negative log-likelihood) 최소화와 동일하다. 이 절에서는 (1) CE가 왜 자연스러운 목표인지, (2) 불균형/어려운 샘플에서 손실을 어떻게 조정하는지, (3) Large-K에서 계산을 가능하게 만드는 근사 학습을 정리한다.
(1) MLE–NLL–Cross-Entropy 연결: ”확률모형을 학습한다”의 의미
데이터 \(\{(x_{i},y_{i})\}_{i = 1}^{n} \sim iid\)이고, 모델이 조건부확률 \(P_{\theta}(Y \mid X)\)를 준다고 하자. 최대우도추정(MLE)은 \(\widehat{\theta} = \arg\max_{\theta}\overset{n}{\prod_{i = 1}}P_{\theta}(y_{i} \mid x_{i})\)이다. 곱은 로그를 취하면 합으로 바뀌면 최적화가 쉬워진다. 그리고 최대화를 최소화로 바꾸기 위해 마이너스를 붙이면 음의 로그우도(NLL) 최소화가 된다.
\[\widehat{\theta} = \arg\min_{\theta}\overset{n}{\sum_{i = 1}}( - \log P_{\theta}(y_{i} \mid x_{i}))\]
다중분류에서 라벨을 원-핫 벡터 \(y_{i} = (y_{i1},\ldots,y_{iK})\)로 쓰고, 모델 확률을 \(p_{i} = (p_{i1},\ldots,p_{iK})\)라 하면 \(- \log P_{\theta}(y_{i} \mid x_{i}) = - \overset{K}{\sum_{k = 1}}y_{ik}\log p_{ik}\). 이 식이 바로 Cross-Entropy(교차엔트로피) 다. 즉 \(\text{MLE} \leftrightarrow \text{NLL 최소화} \leftrightarrow \text{Cross-Entropy 최소화}\)가 한 줄로 연결된다. 딥러닝 분류는 결과적으로 ”확률모형의 최대우도추정”을 SGD로 수행하는 것으로 볼 수 있다.
(2) 다중분류 손실: Softmax + Cross-Entropy
단일정답 다중분류에서 신경망은 로짓 \(\mathbf{z} \in \mathbb{R}^{K}\)를 출력하고 \(p_{k} = \frac{e^{z_{k}}}{\sum_{j = 1}^{K}e^{z_{j}}}\)로 확률을 만든다. 정답이 \(y \in \{ 1,\ldots,K\}\)일 때 CE는 \(\mathcal{L}_{CE}(y,p) = - \log p_{y}\)이며, 원-핫 y를 쓰면 \(\mathcal{L}_{CE}(y,p) = - \overset{K}{\sum_{k = 1}}y_{k}\log p_{k}\)로 정리된다.
직관: ”정답 확률이 작으면 크게 벌점”
\(- \log p_{y}\)는 정답에 부여한 확률 \(p_{y}\)가 작을수록 커진다. 특히 \(p_{y} \rightarrow 0\)이면 손실이 발산하므로, ”정답인데 0에 가깝게 확신하는 예측”을 강하게 교정한다. 이 성질 때문에 CE는 실무에서 매우 강력한 기본 손실로 작동한다.
(3) gradient 직관: (p-y) 형태와 학습 안정성
Cross-Entropy가 널리 쓰이는 이유 중 하나는 softmax와 결합했을 때 기울기가 깔끔해 학습이 안정적이기 때문이다. 한 샘플에 대해 로짓 \(z_{k}\)에 대한 미분은 \(\frac{\partial\mathcal{L}}{\partial z_{k}} = p_{k} - y_{k}\)로 정리된다. 즉 ”예측확률 p”에서 ”정답 y”를 뺀 오차가 그대로 출력층 역전파 신호가 된다.
- 정답 클래스(\(y_{k} = 1\))에서는 \(\frac{\partial\mathcal{L}}{\partial z_{k}} = p_{k} - 1\) → \(p_{k} < 1\)이면 음수이므로 \(z_{k}\)를 키우는 방향으로 업데이트된다.
- 오답 클래스(\(y_{k} = 0\))에서는 \(\frac{\partial\mathcal{L}}{\partial z_{k}} = p_{k}\) → 오답 확률이 클수록 z_k를 줄이는 방향으로 업데이트된다.
이 구조는 ”출력층 오차 신호”가 직관적이고 크기 조절도 잘 되며, 단순 제곱오차를 분류에 억지로 쓰는 것보다 최적화가 유리한 이유를 설명해준다.
(4) 이진분류 손실: BCE(이진 교차엔트로피)
이진분류에서 \(p = P(Y = 1 \mid x)\)라 하면 표준 손실은 \(\mathcal{L}_{BCE}(y,p) = - (y\log p + (1 - y)\log(1 - p))\)이다. CE와 동일한 철학(정답 확률을 높이도록 압박)을 갖지만, 단일 확률 p를 다룬다는 점이 다르다.
(5) 실무 옵션 1: Class weight(불균형 대응)
현장 데이터는 흔히 클래스 불균형(양성이 희귀, 특정 클래스가 압도적으로 많음)을 가진다. 불균형에서 가장 기본 대응은 ”소수 클래스의 손실을 더 크게” 벌점 주는 방식이다.
(A) 다중분류 가중 CE
클래스 가중치를 \(w_{k}\)로 두면 \(\mathcal{L} = - \overset{K}{\sum_{k = 1}}w_{k}y_{k}\log p_{k}\) 정답이 y면 \(\mathcal{L} = - w_{y}\log p_{y}\)가 된다.
(B) 이진분류 가중 BCE
양성 가중치 \(w_{1}\), 음성 가중치 \(w_{0}\)를 두면 \(\mathcal{L} = - (w_{1}y\log p + w_{0}(1 - y)\log(1 - p))\)이다.
가중치를 올리면 대체로 Recall이 좋아질 수 있지만, FP(오경보) 도 함께 늘 수 있다. 즉 학습 목표를 바꾸면 출력 확률/점수의 분포도 변하므로, 운영에서는 임계값 t 를 다시 맞추는 작업이 거의 항상 필요하다.
따라서 불균형 대응은 ”가중치만 주면 끝”이 아니라, 학습(손실) + 운영(임계값/정책) 을 함께 튜닝하는 문제다.
(6) 실무 옵션 2: Label smoothing(과신 완화, 일반화 개선)
원-핫 정답은 ”정답 클래스 확률 1”을 강제하는 성격이 강해, 모델이 과도하게 확신(과신)하도록 만들 수 있다. 이를 완화하기 위해 정답 분포를 조금 부드럽게 만드는 것이 label smoothing이다.
원-핫 y를 다음처럼 바꾼다. \({\overset{˜}{y}}_{k} = (1 - \varepsilon)y_{k} + \frac{\varepsilon}{K}\). 그리고 \(\mathcal{L} = - \overset{K}{\sum_{k = 1}}{\overset{˜}{y}}_{k}\log p_{k}\)로 CE를 계산한다.
효과는 과신 감소하고(확률 보정에 유리한 경우가 많음), 라벨 노이즈에 덜 민감하며, 일부 데이터셋에서 일반화 성능이 개선된다.
단, \(\varepsilon\)가 너무 크면 정답을 지나치게 희석해 성능이 떨어질 수 있어 보통 작은 값(예: 0.05~0.1)을 후보로 둔다.
(7) 불균형과 ”오류비용”은 다른 문제다(학습 vs 운영)
불균형은 데이터에서 양성 비율이 작은 현상(예: \(\pi = P(Y = 1) \ll 1\))이고, 오류비용 비대칭은 ”틀렸을 때 손해가 다름”이다. 예컨대 미탐 비용 \(c_{FN}\)이 크면 양성을 놓치는 것이 치명적이고, 오경보 비용 \(c_{FP}\)이 크면 괜히 양성으로 띄우는 것이 위험하다.
이 비용 비대칭은 운영 단계에서 임계값을 바꾸는 근거가 된다. 대표적으로 \(t^{*} = \frac{c_{FP}}{c_{FP} + c_{FN}}\) 같은 형태로 ”결정 정책”이 바뀐다. 요지는 다음 한 줄이다.
불균형은 ’학습 신호의 희소화’ 문제이고, 비용 비대칭은 ’결정 정책’ 문제다. 둘은 관련은 있지만 동일하지 않다.
(8) 어려운 샘플 대응: focal loss와 hard example mining
불균형 문제에서 모델을 힘들게 하는 것은 ”양성이 적다”뿐 아니라, 실제로는 쉬운 음성(명백히 음성인 샘플) 이 너무 많아 업데이트가 그쪽으로 쏠리는 현상이다. 이때는 ”쉬운 샘플의 영향은 줄이고, 어려운 샘플에 집중”하는 손실 설계가 유효하다.
(A) Focal loss
정답 확률을 \(p_{t}\)라 할 때(이진/다중에서 표기만 달라질 뿐 철학은 동일), focal loss는 \(\mathcal{L}_{focal} = - \alpha(1 - p_{t})^{\gamma}\log(p_{t})\)로 정의된다.
- \(p_{t} \approx 1\)인 쉬운 샘플은 (1-p_t)^\gamma가 매우 작아져 기여가 거의 사라진다.
- \(p_{t}\)가 작은 어려운 샘플은 상대적으로 큰 기여를 갖는다.
결과적으로 결정경계 근처의 샘플이 학습을 더 주도하게 된다.
(B) Hard example mining
손실이 큰 샘플을 더 자주 학습에 포함시키거나, 미니배치에서 손실 상위 일부만 역전파하는 방식으로 ”학습 신호를 어려운 사례에 집중”시킨다.
다만 라벨 노이즈가 있으면 모델이 ”사실 틀린 라벨”을 어려운 샘플로 착각해 과도하게 끌려갈 수 있다. 이 경우 정규화나 label smoothing 같은 안정화가 함께 필요할 수 있다.
(9) Large-K 근사학습: CE를 유지하되 계산을 가능하게 만든다
클래스 수 K가 수만~수백만으로 커지면, softmax와 CE 계산이 병목이 된다. 핵심은 CE가 \(\mathcal{L} = - \log p_{y} = - z_{y} + \log\overset{K}{\sum_{j = 1}}e^{z_{j}}\)이므로 \(\log\sum_{j}e^{z_{j}}\)계산이 기본적으로 O(K)라는 점이다. 또한 출력층 파라미터 \(W \in \mathbb{R}^{K \times d}\) 저장 자체가 O(Kd)로 커져 메모리 병목도 발생한다.
Sampled softmax: ”분모를 일부 클래스만으로 근사”
샘플마다 정답 y와 음성 집합 \(S(|S| = m \ll K)\)를 뽑아 부분 softmax로 근사한다.
\(\log\overset{K}{\sum_{j = 1}}e^{z_{j}} \approx \log(e^{z_{y}} + \sum_{j \in S}e^{z_{j}})\)이로써 클래스 연산이 K\to m으로 줄어 비용이 O(m)이 된다. 다만 근사이므로 샘플링 분포와 보정 방식이 품질에 영향을 준다(편향 감소를 위한 보정항을 넣는 변형들이 존재).
Negative sampling: ”정답 vs 음성”의 대조/랭킹 손실
negative sampling은 softmax 분모를 직접 근사하기보다, 정답쌍 \((x,y)\)와 음성쌍 \((x,j)\)를 구분하도록 학습하는 관점이 강하다. 점수 \(s(x,k)\)에 대해 \(\mathcal{L} = - \log\sigma(s(x,y)) - \sum_{j \in S}\log\sigma( - s(x,j))\)를 사용한다. 직관은 ”정답 점수는 크게, 음성 점수는 작게”다.
음성 샘플링 전략이 성능을 좌우한다.
- 무작위 음성: 너무 쉬워 학습 신호가 약할 수 있음
- 빈도 기반: 자주 나오는 클래스를 더 자주 음성으로
- hard negative: 모델이 헷갈리는 음성
- in-batch negative: 같은 배치의 다른 정답을 음성으로 활용
Large-K에서 종종 ”모델 구조”보다 ”negative 구성”에서 성능 차이가 크게 난다.
3. 분류용 백본 네트워크와 분류 패러다임
앞 절에서는 ”출력층을 어떻게 설계하고(확률모형)“, ”무슨 손실로 학습할지(CE 및 변형)”를 다뤘다. 이제 남는 핵심은 무엇을 분류할 특징으로 만들 것인가이다. 딥러닝 분류 성능의 상당 부분은 입력 x를 표현으로 바꾸는 백본이 결정한다.
또한 분류는 반드시 ”softmax로 확률을 출력”하는 형태만 있는 것이 아니라, 임베딩 공간에서 거리(유사도)로 분류하는 패러다임(=metric learning)으로도 정식화될 수 있다. 특히 Large-K, few-shot, open-set 환경에서는 metric learning이 강한 대안이 된다.
(1) 백본의 역할: 입력을 임베딩으로 바꾸는 공통 구조
딥러닝 분류기는 크게 두 부분으로 생각하면 구조가 단순해진다.
1. 백본(Feature Extractor / Encoder): 입력 x를 임베딩(은닉표현) \(\mathbf{h}\)로 변환한다.
2. 헤드(Classification Head): \mathbf{h}로부터 점수/확률(또는 거리 기반 결정)을 만든다.
이를 수식으로 쓰면 \(\mathbf{h} = f_{\theta}(x) \in \mathbb{R}^{d},\text{(backbone)}\) \(\text{Head}(\mathbf{h}) \Rightarrow \text{score/probability/decision}\)이다.
즉 ”딥러닝 분류를 한다”는 것은 결국 \(f_{\theta}\)가 유용한 임베딩 공간을 만들게 학습하는 것이며, 출력층(softmax/metric)은 그 임베딩을 어떻게 사용할지에 대한 선택이다.
(2) 대표 백본 계열: 데이터 구조에 따라 선택한다
백본은 입력 구조에 맞게 설계된다. 강의노트에서는 ”데이터 타입 → 백본”의 대응으로 정리하는 것이 가장 직관적이다.
MLP(표형 데이터, tabular)
표형 데이터에서는 특성 간 상호작용을 학습하기 위해 완전연결층을 쌓은 MLP가 기본이다. 입력 차원이 크지 않고 구조적 인덕티브 바이어스가 약할 때(표형) 표준 선택이다.
CNN(이미지/격자형)
이미지는 국소 패턴(엣지, 텍스처)과 공간 구조가 핵심이므로 CNN이 강한 인덕티브 바이어스를 제공한다. 합성곱–풀링–계층적 특징 추출을 통해 \mathbf{h}를 만든다.
Transformer(텍스트/시계열/비전)
Transformer는 self-attention을 통해 전역 상호작용을 직접 모델링한다. 텍스트에서는 거의 표준이며, 비전에서도 패치 기반 Transformer가 널리 쓰인다. 긴 의존성이 중요한 시계열에도 적용이 증가한다.
기타: 시계열, 그래프
- 시계열: 1D-CNN, RNN/LSTM, Transformer 계열
- 그래프: GNN 계열(노드/엣지 구조 활용)
요약하면, 백본의 목적은 ”좋은 임베딩 \mathbf{h}“이며, 이후 분류 패러다임(softmax vs metric)이 그 임베딩을 어떤 규칙으로 읽어낼지 결정한다.
(3) 분류 패러다임 1: Softmax(폐집합, 확률분포 기반)
가장 표준적인 분류는 폐집합(closed-set) 가정이다. 학습과 운영에서 클래스 집합이 동일하고, 정답은 그중 하나라고 가정한다. 이때 헤드는 선형 점수 + softmax로 확률분포를 만든다.
\(z_{k} = \mathbf{w}_{k}^{\top}\mathbf{h} + b_{k},k = 1,\ldots,K\). \(p_{k} = \frac{e^{z_{k}}}{\sum_{j = 1}^{K}e^{z_{j}}}\)
이 구조의 장점은 \(\sum_{k}p_{k} = 1\)인 정규화된 확률분포 제공하고 비용민감 의사결정, calibration, thresholding 등 운영 설계에 적합하다. 그리고 Top-1 분류 정확도를 목표로 할 때 정합성이 높다.
반면 단점/한계는 K가 매우 커지면 출력층 계산/메모리가 병목(Large-K)된다. 학습에 없던 클래스가 들어오는 open-set에서는 ”항상 기존 클래스 중 하나로 강제 분류”되는 경향(과신 문제)이 있다.
(4) 분류 패러다임 2: Metric Learning(임베딩 거리 기반 분류)
Large-K 또는 open-set 환경에서는 ”클래스마다 고정된 출력 뉴런(softmax)“을 두는 방식이 비효율적이거나 불가능해진다. 이때 분류를 임베딩 공간에서의 거리/유사도 문제로 바꾸는 접근이 유용하며, 이를 거리학습(metric learning) 이라 한다.
핵심 아이디어: ”가까운 것이 정답”
입력 x를 임베딩으로 보내고, \(\mathbf{h} = f_{\theta}(x) \in \mathbb{R}^{d}\) 같은 클래스는 가깝게, 다른 클래스는 멀게 배치되도록 학습한다. 분류는 확률분포를 직접 출력하기보다, 가장 가까운 클래스(또는 프로토타입) 를 고르는 규칙으로 수행된다.
(A) 최근접(Nearest Neighbor) 분류
클래스 k의 대표 임베딩(학습 샘플 또는 대표점) \(\{\mathbf{c}_{k}\}\)가 있을 때,
\(\widehat{y} = \arg\min_{k}d(\mathbf{h},\mathbf{c}_{k})\text{또는}\widehat{y} = \arg\max_{k}s(\mathbf{h},\mathbf{c}_{k})\), 여기서 d는 거리(예: \(\parallel \mathbf{h} - \mathbf{c} \parallel_{2}\)), s는 유사도(예: cosine similarity)다.
\[\cos(\mathbf{h},\mathbf{c}) = \frac{\mathbf{h}^{\top}\mathbf{c}}{\parallel \mathbf{h} \parallel \parallel \mathbf{c} \parallel}\]
이 방식의 장점은 출력층에 ”K개 뉴런”이 필요 없어서, 클래스가 커지거나 새 클래스가 추가되어도 유연하다는 점이다(임베딩만 추가하면 됨).
(B) 프로토타입(Prototype) 기반 분류
각 클래스 k의 support set \(S_{k}\)가 있을 때, 프로토타입(대표 벡터)을 평균으로 둔다. \(\mathbf{c}_{k} = \frac{1}{|S_{k}|}\sum_{x_{i} \in S_{k}}f_{\theta}(x_{i})\) 그리고 \(\widehat{y} = \arg\min_{k} \parallel \mathbf{h} - \mathbf{c}_{k} \parallel_{2}\)처럼 분류한다. 프로토타입은 클래스 내 변동성을 평균으로 흡수하므로 few-shot에서 특히 자연스럽다.
metric learning 손실: contrastive / triplet
임베딩 공간을 원하는 모양으로 만들려면 ”어떤 쌍/삼쌍은 가깝게, 어떤 것은 멀게”라는 학습 신호가 필요하다. 대표 손실이 contrastive loss 와 triplet loss 다.
(A) Contrastive loss(쌍 기반)
두 샘플 \((x_{i},x_{j})\)에 대해 같은 클래스면 \(y_{ij} = 1\), 다르면 \(y_{ij} = 0\)이라 하자. 거리 \(D_{ij} = \parallel f_{\theta}(x_{i}) - f_{\theta}(x_{j}) \parallel_{2}\)를 정의하면 전형적 형태는 \(\mathcal{L} = y_{ij}D_{ij}^{2} + (1 - y_{ij})\lbrack\max(0,m - D_{ij})\rbrack^{2}\)이다.
같은 클래스 \((y_{ij} = 1)\)는 거리를 0에 가깝게 줄이고, 다른 클래스 \((y_{ij} = 0)\)는 최소 margin m 이상 떨어지도록 만든다. 핵심은 ”음성 쌍은 일정 거리 이상이면 더 밀 필요가 없다”는 margin 개념이다.
(B) Triplet loss(삼쌍 기반)
anchor a, positive p(같은 클래스), negative n(다른 클래스)를 구성한다. 거리 \(D(a,p) = \parallel f(a) - f(p) \parallel_{2},D(a,n) = \parallel f(a) - f(n) \parallel_{2}\)를 두고 목표는 \(D(a,p) + \alpha \leq D(a,n)\)가 되도록 하는 것이다.
손실은 \(\mathcal{L} = \max(0,D(a,p) - D(a,n) + \alpha)\)로 쓴다(\(\alpha\): margin).
triplet loss의 성패는 negative를 어떻게 고르느냐(hard / semi-hard negative mining)에 크게 달려 있다. 너무 쉬운 negative는 학습 신호가 약하고, 너무 어려운 negative(노이즈/오표기 포함)는 학습을 불안정하게 만들 수 있다.
정리하면, contrastive는 ”쌍을 맞추는 문제”, triplet은 ”가까움의 순위(상대 비교)“를 맞추는 문제에 가깝다.
(5) few-shot과 open-set: metric learning이 자연스러운 이유
few-shot 학습과의 연결
few-shot은 클래스당 샘플이 매우 적은 상황이다. softmax 분류는 클래스별 파라미터를 충분히 학습하기 어렵지만, metric learning은 ”임베딩 공간의 일반화”가 핵심이므로 적은 샘플로도 분류 규칙을 만들 수 있다.
특히 프로토타입 방식은 support set으로 \mathbf{c}_k만 계산하면 즉시 동작한다.
open-set / OOD 탐지와의 연결
open-set에서는 학습에 없던 클래스가 들어올 수 있다. softmax는 \(\sum_{k}p_{k} = 1\)을 강제하므로 무엇이 들어와도 기존 클래스 중 하나로 강제 분류하는 경향이 있어 과신 문제가 생길 수 있다.
반면 metric learning은 ”가까운 클래스가 없으면 거리가 멀다”는 신호를 이용해 거절(reject) 규칙을 만들기 쉽다. 예를 들어 최소 거리 기반 거절은 \(\min_{k}d(\mathbf{h},\mathbf{c}_{k}) > \tau \rightarrow \text{unknown}\)처럼 둘 수 있다(유사도 기반이면 \(\max_{k}s(\mathbf{h},\mathbf{c}_{k}) < \tau\) 형태).
(6) 2-stage(retrieval + rerank)와의 연결: Large-K에서의 실전 구조
Large-K 문제에서 ”모든 클래스 K에 대해 softmax 점수를 계산”하는 방식은 학습·서빙 모두에서 계산/메모리 병목이 된다. 대신 실무에서는 목표를 ”정답을 포함하는 후보 집합을 빠르게 좁힌 뒤, 그 안에서 정밀하게 고르는 문제”로 재정식화한다. 이때 metric learning은 1단계 retrieval의 표현(임베딩)을 만드는 핵심 학습 도구가 된다.
Stage 1: Retrieval(후보 생성, high-recall 목표)
목표: 정답을 놓치지 않게 Top-N 후보를 빠르게 회수(recall)한다.
즉 이 단계는 precision보다 recall을 우선한다(”후보에만 들어오면 2단계가 해결한다”).
1. 임베딩 생성: \(\mathbf{h}(x) = f_{\theta}(x) \in \mathbb{R}^{d}\) 입력(쿼리) x를 d차원 임베딩으로 바꾼다. (이미지/텍스트/사용자 행동 등 어떤 입력이든 ”백본+프로젝션 헤드”로 \mathbf{h}를 만든다.)
2. 클래스/아이템 임베딩 테이블: 각 후보 k (상품/문서/광고/클래스)를 임베딩 \(\mathbf{e}_{k} \in \mathbb{R}^{d}\)로 둔다.
분류 관점에서는 ”클래스 프로토타입”
추천/검색에서는 ”아이템 임베딩”
3. 유사도 점수와 Top-N 검색: 보통 내적이나 cosine을 쓴다. \(s(x,k) = \mathbf{h}(x)^{\top}\mathbf{e}_{k}\text{(또는)}s(x,k) = \cos(\mathbf{h}(x),\mathbf{e}_{k})\). 이 점수로 \(\mathcal{C}_{N}(x) = \text{Top-}N\{ s(x,k)\}_{k = 1}^{K}\)을 찾는다.
4. ANN(Approximate Nearest Neighbor): 인덱스 K가 매우 크면 정확한 Top-N 탐색이 어렵다. 그래서 근사 최근접 탐색(ANN) 인덱스를 구축한다.
IVF/HNSW/ScaNN/FAISS류 방법을 사용해 ”거의 Top-N”을 매우 빠르게 찾는다.
운영에서는 지연시간(latency) 과 recall@N 사이의 트레이드오프를 튜닝한다.
5. Stage 1에서 무엇을 학습하나(핵심): Stage 1은 ”정답 임베딩이 쿼리 임베딩에 더 가깝게” 되도록 학습한다. 전형적으로 contrastive / triplet / in-batch negative 혹은 샘플링 기반 softmax(큰 후보공간에서 분모를 근사)를 쓴다. 중요한 건 음성 설계가 곧 retrieval 성능을 좌우한다는 점이다(쉬운 음성만 쓰면 retrieval이 약해짐).
무엇을 언제 쓰나? Softmax 분류 vs Metric Learning 선택 기준
둘 다 ”분류”지만 전제가 다르다. 아래 체크리스트로 선택하면 실무적으로 안정적이다.
Stage 2: Rerank(정밀 재정렬, high-precision 목표)
Stage 2는 Stage 1이 만든 후보 집합 \(\mathcal{C}(x)\) 내부에서 더 정밀하게 최종 순위를 결정하는 단계이다. 후보 수는 \(N\ll K\) 이므로, Stage 2에서는 Stage 1보다 더 비싼 특징과 더 강한 모델을 사용할 수 있다.
정밀 점수 계산: 후보 \(k\in\mathcal{C}(x)\) 에 대해 재점수화 함수 \(s_2(x,k)\) 를 계산한다. 이 점수는 쿼리–후보의 교차 특징(cross feature), 문맥 정보, 메타데이터(가격/재고/시간/정책 점수 등)까지 포함할 수 있다. \(\widehat{k}=\arg\max_{k\in\mathcal{C}(x)} s_2(x,k)\)
대표적인 Stage 2 설계
- 후보집합 softmax: 후보 집합 안에서만 정규화하여 “확률적 선택”으로 해석한다. \(p(k\mid x,\mathcal{C})=\frac{\exp(s_2(x,k))}{\sum_{j\in\mathcal{C}(x)}\exp(s_2(x,j))}\)
- 랭킹 학습(pairwise/listwise): 정렬 품질(NDCG 등)에 직접 맞춘다.
- cross-encoder / deep interaction 모델: [x;k]를 함께 넣어 상호작용을 강하게 반영한다(특히 텍스트 검색에서 유효하다).
- 후처리(정책/제약 반영): 금지 항목 필터링, 다양성, 중복 제거, 최신성 가중 등 운영 규칙을 최종 단계에서 함께 반영하는 경우가 많다.
- Stage 2를 생략하는 경우: 서비스 목표가 “유사 항목 제시”처럼 Stage 1의 Top-N 자체가 충분히 좋은 결과인 경우에는 Stage 2를 생략하기도 한다. 다만 “Top-1 정답 선택”이나 “상위 몇 개의 정밀도”가 핵심인 문제에서는 Stage 2가 품질을 안정화하는 역할을 하므로, 일반적으로 두 단계를 함께 두는 편이 강건하다.
(7) 무엇을 언제 쓰나? Softmax 분류 vs Metric Learning 선택 기준
둘 다 “분류”지만 전제가 다르다. 아래 체크리스트로 선택하면 실무적으로 안정적이다.
Softmax(+CE)를 우선 선택하는 경우
- 클래스가 고정된 폐집합(closed-set) 이고 학습/운영에서 동일한 클래스 집합을 사용한다.
- 확률 \(P(Y = k \mid x)\) 자체가 필요하다(리스크 스코어링, 비용기반 의사결정, calibration 운영 등). \(\sum_{k}p_{k} = 1\)인 확률분포가 자연스럽다.
- 클래스당 데이터가 충분하여 출력층 파라미터가 안정적으로 추정된다.
- 목표가 Top-1 정확도 중심이고 ”unknown 거절”이 운영 요구가 아니다.
Metric Learning을 우선 선택하는 경우
- 새 클래스가 자주 추가/변경되거나, 학습 시점에 모든 클래스를 다 보지 못한다. softmax 출력층(\(K \times d\))을 계속 재학습하기 어렵다.
- few-shot(클래스당 샘플이 매우 적음)에서 빠르게 적응해야 한다.프로토타입 + 최근접 분류가 강력하다. open-set/unknown 거절이 중요하다. \(\min_{k}d(\mathbf{h},\mathbf{c}_{k}) > \tau\) 같은 규칙이 자연스럽다.
- 문제의 본질이 검색/추천/유사도 질의(retrieval)이고 Top-k/랭킹 지표가 핵심이다. 임베딩 + ANN + rerank(2-stage)로 확장성이 좋다.
실무 결론(하이브리드도 흔함)
- ”폐집합 분류 + 확률 필요”이면 softmax(+CE)로 가고, calibration/threshold 정책까지 함께 설계한다.
- ”대규모/동적/검색형”이면 metric learning으로 임베딩을 만들고 retrieval+r erank로 운영한다.
- 하이브리드로, 임베딩 기반 retrieval로 후보를 줄인 뒤 후보에 대해 softmax(또는 pairwise scoring)로 rerank/확률화하는 구조도 흔하다.
(8) 대조학습(Contrastive Learning) ↔︎ Metric Learning ↔︎ 사전학습 파이프라인
metric learning은 겉으로는 ”거리 기반 분류”처럼 보이지만, 본질적으로는 임베딩 공간을 학습하는 표현학습 이다.
같은 클래스(또는 같은 의미)의 샘플은 가깝게, 다른 클래스는 멀게 배치하도록 학습한다는 점에서, contrastive loss / triplet loss는 대조학습(contrastive learning) 의 대표적 형태로 볼 수 있다. 즉, ”분류기를 바로 학습”하기보다 먼저 좋은 임베딩 \(f_{\theta}(x)\)을 만들고, 그 임베딩 위에서 최근접/프로토타입/랭킹으로 분류 또는 검색을 수행한다.
이 관점은 최근 딥러닝의 표준 파이프라인인 사전학습(pretraining) → 다운스트림 분류(finetune/linear probe) 와 직접 연결된다.
사전학습 단계에서는 레이블이 없거나 약한 상황에서도, 데이터 쌍(positive/negative)을 구성해 다음과 같은 목표를 최적화한다.
- positive(유사/동일 의미) 쌍은 유사도 증가
- negative(다른 의미) 쌍은 유사도 감소
예를 들어 \(\mathcal{L} = - \log\sigma(s(x,x^{+})) - \sum_{j}\log\sigma( - s(x,x_{j}^{-}))\)와 같은 형태로 학습된 임베딩은 라벨이 적은 상황(few-shot), 클래스가 자주 바뀌는 동적 카탈로그, Large-K 검색/추천에서 특히 강력하다.
이후 다운스트림에서는 (i) 임베딩을 고정한 채 얕은 분류기만 학습(linear probe)하거나, (ii) 전체를 미세조정(fine-tuning)하여 softmax 분류기로 마무리하는 방식이 가능하다.
4. 일반화와 정규화: 과적합을 줄이고 ”과신”을 완화하는 설계
딥러닝 분류의 성능은 훈련 데이터에서의 정확도가 아니라, 보지 못한 새 데이터에서 얼마나 잘 작동하는가(일반화)로 평가된다. 신경망은 표현력이 매우 커서 훈련 데이터를 거의 외우는 수준까지도 도달할 수 있으므로, 훈련 손실이 계속 내려간다고 해서 실제 운영 성능이 보장되지는 않는다.
특히 분류에서는 과적합이 단순한 ”테스트 정확도 하락”에 그치지 않고, 예측 확률이 0 또는 1에 가깝게 치우치는 과신으로 동반되는 경우가 많다. 따라서 일반화/정규화는 정확도뿐 아니라 확률의 신뢰도(calibration)까지 염두에 둔 설계로 이해하는 것이 중요하다.
일반화의 목표: 경험위험 최소화 vs 테스트 위험 최소화
훈련 데이터 \(\{(x_{i},y_{i})\}_{i = 1}^{n}\)에 대해 분류 모델은 보통 훈련 손실(경험위험)을 최소화한다. \(\widehat{\theta} = \arg\min_{\theta}\frac{1}{n}\overset{n}{\sum_{i = 1}}\mathcal{L}(y_{i},f_{\theta}(x_{i}))\)
그러나 우리가 진짜로 줄이고 싶은 것은 훈련셋이 아니라 모집단 분포에서의 손실(테스트 위험)이다.
\[\mathcal{R}(\theta) = \mathbb{E}_{(X,Y)}\lbrack\mathcal{L}(Y,f_{\theta}(X))\rbrack\]
훈련 손실을 낮추는 것은 \(\mathcal{R}(\theta)\)를 낮추기 위한 대리 목적이지만, 모델 용량이 충분히 크면 훈련 손실만 과도하게 낮추면서 오히려 \(\mathcal{R}(\theta)\)를 악화시키는 과적합이 쉽게 발생한다. 일반화의 핵심은 ”훈련을 잘하는 것”이 아니라 ”훈련을 통해 테스트 위험을 줄이는 것”이다.
과적합의 전형적 징후: 정확도 문제와 과신의 동반
과적합은 보통 다음과 같은 형태로 드러난다. 훈련 손실은 계속 감소하지만 검증 손실은 어느 시점부터 증가하며, 훈련 정확도는 매우 높아지는 반면 테스트 정확도는 정체하거나 하락한다.
동시에 예측 확률이 극단으로 치우치며, 틀린 예측에도 \(p \approx 0.99\) 같은 높은 확률을 부여하는 과신이 나타나기도 한다.
과신이 과적합과 함께 나타나는 이유는 구조적으로 설명할 수 있다. 다중분류에서 softmax는 \(\sum_{k}p_{k} = 1\)이라는 경쟁 구조를 만들고, cross-entropy는 정답 확률 \(p_{y}\)를 1 쪽으로 밀어붙이는 손실이다.
\[\mathcal{L} = - \log p_{y}\]
데이터가 쉽게 분리되거나 모델 용량이 과도하면 로짓 격차가 커지고, softmax는 최대 클래스 확률을 급격히 1에 가깝게 만든다. 이때 결정경계 밖에서 확률이 극단화되며, 분포 이동이나 OOD 입력이 존재하는 운영 환경에서는 이러한 과신이 특히 위험해진다.
정규화의 큰 축: 복잡도 억제와 학습 안정화
일반화 성능을 개선하는 실무적 레버는 크게 두 가지로 정리된다. 하나는 모델이 훈련 데이터에 과도하게 맞춰지는 것을 직접 억제하는 복잡도 억제(명시적 정규화)이고, 다른 하나는 학습을 안정화해 결과적으로 더 좋은 해에 도달하게 하는 학습 안정화(최적화 관점의 안정화)이다.
복잡도 억제 1: 가중치 규제(Weight decay, L_2)
가장 보편적인 정규화는 가중치 크기를 억제하는 것이다. 전형적으로 손실에 \(L_{2}\) 페널티를 더해 \(\min_{\theta}\frac{1}{n}\overset{n}{\sum_{i = 1}}\mathcal{L}(y_{i},f_{\theta}(x_{i})) + \lambda \parallel \theta \parallel_{2}^{2}\)를 최소화한다. 직관적으로 weight decay는 가중치를 과도하게 키워 결정경계를 지나치게 날카롭게 만드는 경향을 완화하며, 결과적으로 예측 확률의 극단화(과신)도 줄어드는 방향으로 작용할 수 있다.
실무에서는 AdamW와 같은 옵티마이저와 함께 쓰는 경우가 많고, 데이터가 작거나 노이즈가 있을수록 중요해진다.
복잡도 억제 2: 드롭아웃(Dropout)
드롭아웃은 학습 중 일부 뉴런을 확률적으로 제거하여 공적응(co-adaptation)을 억제한다. 이는 모델이 특정 특징 조합에 과도하게 의존하지 않고, 보다 일반적인 표현을 학습하도록 유도하는 효과가 있다. 구현이 단순하고 과적합 완화에 효과적이지만, 배치정규화(BN)와 동시에 사용할 때는 적용 위치와 강도 등 세부 튜닝이 필요할 수 있다.
과신 관점에서도 드롭아웃은 결정경계를 덜 날카롭게 만들어 확률의 극단화를 완화하는 데 도움이 되는 경우가 있다. 다만 드롭아웃만으로 calibration이 자동으로 보장되지는 않으므로, 필요하면 사후 보정(temperature scaling 등)과 함께 보는 것이 안전하다.
복잡도 억제 3: 조기 종료(Early stopping)
조기 종료는 검증 손실이 나빠지기 시작하면 학습을 멈추는 방식으로, 복잡한 정규화 없이도 과적합을 막는 매우 강력한 도구다. 훈련 손실은 내려가는데 검증 손실이 증가한다면 그 시점 이후는 과적합 구간으로 보는 것이 자연스럽고, 최적 epoch는 ”훈련이 끝난 시점”이 아니라 ”검증 성능이 가장 좋은 시점”이 된다.
과신과의 연결에서도, 학습을 오래 지속하면 로짓 규모가 계속 커지며 확률이 극단화되는 경향이 있으므로, 조기 종료가 과신을 완화하는 경우가 많다.
복잡도 억제 4: Label smoothing(과신 완화 정규화)
label smoothing은 손실 옵션이면서 동시에 정규화로 볼 수 있다. 원-핫 정답을 부드럽게 만들어 ”정답 확률 1을 강제”하는 압박을 줄인다.
\[{\overset{˜}{y}}_{k} = (1 - \varepsilon)y_{k} + \frac{\varepsilon}{K},\mathcal{L} = - \overset{K}{\sum_{k = 1}}{\overset{˜}{y}}_{k}\log p_{k}\]
이 기법은 과신을 줄이고 라벨 노이즈에 덜 민감하게 만들며, 일부 데이터셋에서는 일반화 성능을 개선한다. 다만 \varepsilon이 너무 크면 정답이 과도하게 희석되어 성능이 하락할 수 있어, 보통 작은 값을 후보로 두고 튜닝한다. 핵심은 label smoothing이 정확도뿐 아니라 확률 품질에도 영향을 주는 대표적 학습 단계 기법이라는 점이다.
학습 안정화: BatchNorm과 최적화 안정성이 일반화로 이어지는 경우
배치정규화(BatchNorm)는 층의 활성값 분포를 정규화해 학습을 안정화하는 기법이다. 최적화가 안정되면 더 좋은 해로 수렴하거나 학습이 덜 흔들려 일반화 성능이 함께 좋아지는 경우가 많다. 또한 학습률이나 초기화에 대한 민감도를 낮춰 실무에서 튜닝 부담을 줄여준다.
다만 BN이 calibration을 자동으로 해결하는 것은 아니다. BN은 학습 과정의 안정화이고 calibration은 확률 해석의 품질이므로, 확률 품질은 후속 절에서 별도로 점검·보정하는 것이 원칙이다.
데이터 규모와 모델 규모: 환경에 따라 전략이 달라진다
일반화 전략은 대체로 ”데이터가 작을수록 정규화를 강하게, 데이터가 클수록 표현력을 확보”라는 흐름을 따른다. 데이터가 작으면 모델을 단순화하고(파라미터 수 감소), 정규화를 강하게 적용하며(weight decay↑, dropout↑), 조기 종료를 적극적으로 쓰고, 사전학습/전이학습 비중을 높이는 것이 안전하다.
반대로 데이터가 충분히 크면 모델 규모를 키워 표현력을 확보하되, 정규화는 성능 극대화보다는 안정성 확보 관점에서 조절한다.
특히 작은 데이터에서 큰 모델을 쓰면 훈련에서는 매우 높은 확률로 맞히는 것처럼 보이지만, 운영에서는 과신과 오경보가 커지는 문제가 자주 발생한다.
정규화와 과신: ”학습 단계 개선 + 사후 보정”의 2단 접근
과신은 softmax 구조, CE 학습 압력, 데이터/학습 환경이 결합된 결과로 보는 것이 정확하다. 따라서 실무에서는 두 단계 접근이 안정적이다.
먼저 학습 단계에서 정규화(가중치 규제, 드롭아웃, 조기 종료, label smoothing, 증강, 전이학습 등)로 일반화와 과신을 완화하고, 이후 사후 단계에서 calibration(temperature scaling, Platt scaling, isotonic 등)으로 확률을 보정한다. 정규화만으로 확률이 완벽히 보정되길 기대하기보다, 일반화 개선과 사후 보정을 함께 설계하는 것이 운영 관점에서 안전하다.
실전 체크리스트: 무엇부터 조절할까?
훈련 성능과 검증 성능의 격차가 커지면 조기 종료를 먼저 점검한다. 데이터가 작거나 노이즈가 크면 weight decay를 우선 강화하고, 필요하면 label smoothing을 소량 적용하며 dropout을 병행한다.
학습이 불안정하면 학습률/스케줄과 BatchNorm 등 학습 안정화 요소를 점검한다. 정확도는 괜찮은데 과신이 심하다면, 학습 단계에서 정규화·증강·label smoothing을 강화한 뒤에도 문제가 남는지 확인하고, 운영 단계에서는 temperature scaling 같은 calibration과 threshold 재설계를 함께 수행한다.
5. 사전학습/자기지도/대조학습 후 분류기
현대 딥러닝 분류는 ”처음부터 끝까지 supervised 학습”만으로 설명되기 어렵다. 특히 이미지·텍스트 모두에서 (i) 강한 데이터 증강, (ii) 사전학습(pretraining), (iii) 전이학습(transfer learning)이 표준 파이프라인이 되었고, 분류기는 종종 ”잘 학습된 표현(representation) 위에 얹는 얕은(head)” 형태로 구현된다.
여기에서는 CNN 기반 이미지 분류의 기본 구조를 정리하고, 증강과 전이학습이 왜 일반화와 calibration에까지 영향을 주는지, 그리고 문서 분류에서의 전형적 파이프라인을 함께 연결한다.
(1) CNN(합성곱) 기반 딥러닝 분류
신경망은 2010년 무렵 이미지 분류에서 큰 성공을 거두면서 다시 주목받기 시작했다. 그 당시에는 라벨이 붙은 이미지로 이루어진 대규모 데이터베이스가 빠르게 축적되고 있었고, 클래스 수도 계속 증가하고 있었다.
다음 그림은 CIFAR100 데이터베이스에서 뽑은 75장의 이미지를 보여준다. 이 데이터베이스는 20개의 상위 범주(예: 수생 포유류)로 구분된 60,000장의 이미지로 구성되며, 각 상위 범주마다 5개의 클래스(예: 비버, 돌고래, 수달, 물개, 고래)가 있다.
각 이미지는 32×32 픽셀의 해상도를 가지며, 각 픽셀은 빨강(red), 초록(green), 파랑(blue)을 나타내는 8비트 숫자 3개로 표현된다. 각 이미지의 숫자들은 특징맵(feature map)이라 불리는 3차원 배열로 정리된다. 앞의 두 축은 공간 축(둘 다 길이 32)이고, 세 번째 축은 세 가지 색을 나타내는 채널(channel) 축이다. 학습용(training) 세트는 50,000장, 테스트(test) 세트는 10,000장으로 지정되어 있다.
이러한 이미지들을 분류하기 위해 합성곱 신경망(CNN)이라는 특수한 신경망 계열이 발전해 왔으며, 매우 다양한 문제에서 뛰어난 성과를 보여 왔다. CNN은 이미지 속 어디에서든 특정 특징이나 패턴을 인식함으로써, 어느 정도는 인간이 이미지를 분류하는 방식과 유사하게 작동한다.
이미지 분류에서 CNN은 ”공간적 구조를 활용해 특징을 계층적으로 추출”하는 대표 모델이다. 입력 \(X \in \mathbb{R}^{H \times W \times C}\)에 대해, CNN은 국소 영역을 공유 가중치로 스캔하며(feature sharing) 특징맵(feature map)을 만든다. 이는 완전연결(FC)보다 파라미터 효율이 높고, 위치 변화에 더 강건한 표현을 학습하게 한다.
Convolutional Layers (합성곱 층)
합성곱 층은 많은 수의 합성곱 필터로 구성된다. 각 필터는 이미지 안에 특정한 국소 특징이 존재하는지를 판별하는 템플릿 역할을 한다. 합성곱 필터는 합성곱이라 불리는 매우 단순한 연산에 기반하며, 이는 기본적으로 행렬 원소들을 반복적으로 곱한 뒤 그 결과를 더하는 작업으로 이루어진다.
합성곱 필터가 어떻게 작동하는지 이해하기 위해, 아주 단순한 \(2 \times 3\)이미지 예를 생각해보자.
\(\text{Original Image} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \\ j & k & l \end{bmatrix}\). 다음의 \(2 \times 2\) 필터 \(\text{Convolution Filter} = \begin{bmatrix} \alpha & \beta \\ \gamma & \delta \end{bmatrix}\)로 이미지를 합성곱하면 다음 결과를 얻는다. 예를 들어, 왼쪽 위 원소는 \(2 \times 2\) 필터의 각 원소를 이미지의 왼쪽 위 \(2 \times 2\) 부분과 대응시키며 곱한 뒤 그 결과를 합하여 얻는다. 다른 원소들도 동일한 방식으로 얻어진다.
\[\text{Convolved Image} = \begin{bmatrix} a\alpha + b\beta + d\gamma + e\delta & b\alpha + c\beta + e\gamma + f\delta \\ d\alpha + e\beta + g\gamma + h\delta & e\alpha + f\beta + h\gamma + i\delta \\ g\alpha + h\beta + j\gamma + k\delta & h\alpha + i\beta + k\gamma + l\delta \end{bmatrix}\]
즉, 합성곱 필터를 원본 이미지의 모든 \(2 \times 2\) 부분행렬에 적용함으로써 합성곱된 이미지를 만든다. 원본 이미지의 어떤 \(2 \times 2\) 부분행렬이 합성곱 필터와 비슷하다면, 합성곱된 이미지에서 해당 위치의 값은 크게 나타나고, 그렇지 않다면 작게 나타난다.
따라서 합성곱된 이미지는 원본 이미지에서 합성곱 필터와 유사한 영역을 강조(highlight)한다. 여기서는 \(2 \times 2\)를 예로 들었지만, 일반적으로 합성곱 필터는 \(\ell_{1} \times \ell_{2}\) 크기의 작은 배열이며, \(\ell_{1},\ell_{2}\) 는 (반드시 같을 필요는 없는) 작은 양의 정수이다.
다음 그림은 왼쪽에 있는 \(192 \times 179\) 크기의 호랑이 이미지에 두 개의 합성곱 필터를 적용하는 예를 보여준다. 각 합성곱 필터는 \(15 \times 15\) 크기의 이미지로, 대부분은 0(검정)이며 이미지 안에서 세로 또는 가로 방향으로 놓인 1(흰색)의 좁은 띠를 포함한다. 각 필터를 호랑이 이미지에 합성곱하면, 필터와 유사한(즉 세로/가로 줄무늬나 에지를 가진) 영역에는 큰 값이 부여되고, 해당 특징과 닮지 않은 영역에는 작은 값이 부여된다.
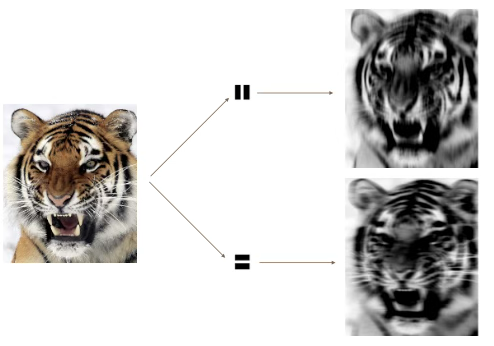
합성곱 필터는 에지(edge)나 작은 모양처럼 이미지의 국소 특징을 찾아낸다. 왼쪽의 호랑이 이미지에 가운데의 두 개 작은 합성곱 필터를 적용한다. 합성곱된 이미지는 원본 이미지에서 필터와 비슷한 세부 구조가 발견되는 영역을 강조한다.
구체적으로 위쪽 합성곱 결과는 호랑이의 세로 줄무늬를 강조하고, 아래쪽 합성곱 결과는 가로 줄무늬를 강조한다. 원본 이미지를 합성곱 신경망의 입력층으로, 합성곱된 이미지들을 첫 번째 은닉층의 유닛들로 생각할 수 있다.
합성곱 층에서는 서로 다른 방향의 에지와 형태를 다양하게 골라내기 위해 필터들의 전체 집합(bank)을 사용한다. 이러한 방식으로 미리 정의된 필터를 쓰는 것은 전통적인 이미지 처리에서 표준적 관행이다.
반면 CNN에서는 필터가 특정 분류 과제를 위해 학습된다. 필터의 가중치는 입력층에서 은닉층으로 가는 모수로 생각할 수 있는데, 합성곱된 이미지의 각 픽셀마다 하나의 은닉 유닛이 대응된다고 보면 된다.
실제로도 그렇지만, 이 모수들은 매우 구조화되고 제약된 형태를 가진다. 즉 입력 이미지의 국소 패치에만 작동하므로 구조적으로 0인 부분이 많고, 하나의 필터 안에서 같은 가중치가 이미지의 모든 가능한 위치에 재사용되므로(가중치가 공유되므로) 가중치가 제약된다.
입력 이미지가 컬러이므로, 3차원 특징맵(배열)로 표현되는 세 개의 채널을 가진다. 각 채널은 \(32 \times 32\)의 2차원 특징맵이며, 각각 빨강(red), 초록(green), 파랑(blue)에 해당한다.
하나의 합성곱 필터도 마찬가지로 색상별로 하나씩, 총 세 개의 채널을 가지며, 각 채널은 \(3 \times 3\) 크기이고 채널마다 필터 가중치가 달라질 수 있다.
이 세 번의 합성곱 결과를 합산하여 하나의 2차원 출력 특징맵을 만든다. 이 시점에서는 색상 정보가 이미 사용되었고, 이후 층으로는(합성곱에서의 역할을 제외하면) 별도로 전달되지 않는다.
첫 번째 은닉층에서 서로 다른 합성곱 필터를 K개 사용하면, K개의 2차원 출력 특징맵을 얻게 된다. 이들은 함께 하나의 3차원 특징맵으로 취급된다.
우리는 K개의 출력 특징맵 각각을 서로 다른 정보 채널로 보며, 따라서 원래 입력 특징맵의 3개 색상 채널과 대비되어 이제는 K개의 채널을 갖게 된다. 이 3차원 특징맵은 단순 신경망 은닉층의 활성값(activations)과 유사하지만, 공간적으로 구조화된 방식으로 정리되고 생성된다는 점이 다르다.
보통 합성곱된 이미지에 ReLU 활성함수를 적용한다. 이 단계는 때로 CNN의 별도 층으로 간주되며, 그런 경우 detector layer(검출기 층)라고 부르기도 한다.
Pooling Layers
풀링 층(pooling layer)은 큰 이미지를 더 작은 요약 이미지로 압축(condense)하는 방법을 제공한다. 풀링에는 여러 방식이 가능하지만, 맥스 풀링(max pooling)은 이미지의 겹치지 않는 각 \(2 \times 2\) 블록을 그 블록 안의 최댓값으로 요약한다.
이 연산은 이미지의 크기를 각 방향에서 2배씩 줄이며(즉 가로/세로 모두 절반), 동시에 어느 정도의 위치 불변성(location invariance)을 제공한다. 즉 블록 안의 4개 픽셀 중 하나라도 큰 값이 있으면, 축소된 이미지에서는 그 블록 전체가 큰 값으로 기록된다.
맥스 풀링의 간단한 예는 다음과 같다.
\[\text{Max pool}\begin{bmatrix} 1 & 2 & 5 & 3 \\ 3 & 0 & 1 & 2 \\ 2 & 1 & 3 & 4 \\ 1 & 1 & 2 & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 3 & 5 \\ 2 & 4 \end{bmatrix}\]
CNN Architecture
지금까지 우리는 하나의 합성곱 층을 정의했다. 각 필터는 새로운 2차원 특징맵 하나를 만든다. 합성곱 층에서 필터의 개수는, 완전연결 신경망에서 특정 은닉층의 유닛 수와 유사한 역할을 한다.
이 수는 또한 결과로 생성되는 3차원 특징맵의 채널 수를 결정한다. 또한 풀링 층은 각 3차원 특징맵의 앞 두 차원(공간 차원)을 줄인다는 것을 설명했다. 깊은 CNN은 이러한 층을 많이 쌓는다.
다음 그림은 CIFAR100 이미지 분류 과제를 위한 CNN의 전형적인 구조를 보여준다. CIFAR100 분류 과제를 위한 깊은 CNN의 아키텍처. 합성곱 층들 사이에 \(2 \times 2\) 맥스풀 층이 끼워져 있으며, 맥스풀은 두 공간 차원 모두에서 크기를 2배씩 줄인다.
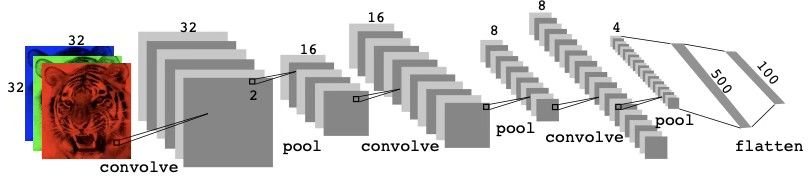
입력층에서는 컬러 이미지의 3차원 특징맵을 보게 되는데, 여기서 채널 축은 각 색을 \(32 \times 32\)의 2차원 픽셀 특징맵으로 나타낸다.
첫 번째 은닉층에서 각 합성곱 필터는 새로운 채널을 하나씩 만들어내며, 각각은(가장자리에 패딩을 약간 준 뒤) \(32 \times 32\) 특징맵이 된다.
첫 번째 합성곱을 마치면 우리는 새로운 ”이미지”, 즉 입력의 3개 색상 채널보다 훨씬 많은 채널을 가진 특징맵을 얻게 된다(그림에서는 합성곱 필터를 6개 사용했기 때문에 채널이 6개).
그 다음에는 맥스풀 층이 이어지며, 이는 각 채널의 특징맵 크기를 4분의 1로 줄인다(각 방향에서 2배씩 줄어드는 것과 같다). 이런 ”합성곱→풀링” 순서는 다음 두 층에서도 반복된다.
세부 사항은 다음과 같다. 이후의 각 합성곱 층은 첫 번째 층과 유사하다. 이전 층의 3차원 특징맵을 입력으로 받아 이를 하나의 다채널 이미지처럼 취급한다. 학습되는 각 합성곱 필터는 이 특징맵과 동일한 수의 채널을 가진다.
풀링 층을 거치면 채널 특징맵의 공간 크기가 줄어드므로, 보통 이를 보상하기 위해 다음 합성곱 층에서 필터 수를 늘린다.
때로는 풀링 층을 넣기 전에 합성곱 층을 여러 번 반복한다. 이는 사실상 필터의 차원을(표현력을) 증가시키는 효과가 있다.
이 연산들은 풀링을 통해 각 채널 특징맵이 각 차원에서 몇 픽셀만 남을 때까지 반복된다. 이 시점에서 3차원 특징맵은 flatten되어(픽셀을 개별 유닛으로 취급) 하나 이상의 완전연결 층으로 들어가며, 최종적으로 출력층에 도달한다. 출력층은 100개 클래스에 대한 softmax 활성함수를 사용한다.
이런 네트워크를 구성할 때는 각 층의 개수·종류·크기 외에도 선택해야 할 튜닝 파라미터가 많다. 드롭아웃(dropout)은 각 층에서 사용할 수 있고, 라쏘(lasso)나 릿지(ridge) 정규화도 사용할 수 있다. 합성곱 신경망을 구성하는 세부 사항은 부담스럽게 느껴질 수 있다.
다음 그림은 데이터 증강(data augmentation)으로 원본 이미지(가장 왼쪽)를 자연스러운 방식으로 왜곡하여 같은 클래스 레이블을 갖는 서로 다른 이미지를 만든다. 이러한 왜곡은 사람을 속이지 않으며, CNN을 적합할 때 정규화(regularization)의 한 형태로 작동한다.

(2) Data Augmentation
데이터 증강은 ”라벨을 유지하는 변환으로 학습 데이터를 확장”하여 일반화 성능을 높이는 핵심 기법이다. 증강은 단순히 데이터 수를 늘리는 것 이상으로, 모델에게 불변성(invariance) 또는 평활한 결정경계를 학습시키는 역할을 한다.
기본 증강(flip/crop/rotate/color jitter)
- flip: 좌우 반전 (대칭성이 있는 문제에서 유효)
- random crop / resize: 위치/스케일 변화에 강건
- rotate: 회전 불변성이 있는 경우 유효(과도한 회전은 라벨 의미를 바꿀 수 있음)
- color jitter: 밝기/대비/채도 변형으로 조명 변화에 강건
증강의 본질은 ”입력 공간에서 같은 라벨을 갖는 영역을 넓혀” 과적합을 줄이는 것이다.
강한 증강/혼합(mixup/cutmix 등, 선택)
강한 증강은 일반화를 크게 올릴 수 있지만, 과하면 학습이 어려워지거나 과소적합을 유발할 수 있어 데이터/도메인에 맞춰 조절한다.
- mixup: 두 샘플과 라벨을 선형 결합 \(\overset{˜}{x} = \lambda x_{i} + (1 - \lambda)x_{j},\overset{˜}{y} = \lambda y_{i} + (1 - \lambda)y_{j}\) 이는 결정경계를 더 선형/평활하게 만들어 과신을 줄이고(calibration 개선 사례 많음), 노이즈에 강해질 수 있다.
- cutmix: 한 이미지의 일부 패치를 다른 이미지로 교체하고, 면적 비율로 라벨을 혼합
라벨 혼합이 ”공간적 부분”과 대응하므로 이미지 분류에서 효과가 좋은 경우가 많다.
(3) Pretrained Model & Transfer Learning(전이학습)
사전학습 모델은 대규모 데이터로 학습된 표현을 제공하며, 작은 데이터에서도 강력한 출발점을 만든다. 특히 CNN/Transformer 모두에서 ”표현 학습은 대규모로, 과제별 분류기는 소규모로”가 표준이 되었다.
feature extraction vs fine-tuning
Feature extraction(특징 추출): backbone g_\theta는 고정하고, head만 학습 \(\mathbf{h} = g_{\theta_{0}}(x),\min_{W}\sum_{i}\mathcal{L}(y_{i},softmax(W\mathbf{h}_{i}))\) 장점으로는 빠르고 과적합 위험이 낮다(특히 데이터가 작을 때).
Fine-tuning(미세조정): backbone까지 함께 업데이트 \(\min_{\theta,W}\sum_{i}\mathcal{L}(y_{i},softmax(Wg_{\theta}(x_{i})))\) 장점은 도메인 적응력이 커서 최종 성능이 더 좋아지기 쉽고 단점으로는 데이터가 작으면 과적합/과신이 커질 수 있어 정규화/증강이 중요하다.
작은 데이터에서의 실무 절차(동결→점진적 unfreeze)
작은 데이터에서 흔히 쓰는 안정적 절차는 다음이다.
1. head만 학습(backbone 동결) → 빠르게 베이스라인 확보
2. 성능이 정체되면 상위 블록부터 점진적 unfreeze
3. backbone 학습률은 head보다 작게(예: \(\eta_{\text{backbone}} \ll \eta_{\text{head}}\))
4. 증강/weight decay/early stopping으로 과적합 제어
5. 필요 시 calibration(temperature scaling)과 임계값 재튜닝까지 묶어서 운영 성능 정리
(4) Document Classification(문서 분류)
문서 분류는 ”텍스트를 어떤 표현으로 바꾸고, 그 위에 분류기를 얹는다”는 점에서 이미지와 동일한 구조를 가진다. 다만 표현 방식이 BoW/TF-IDF 같은 고전적 희소 벡터에서, Transformer 기반 문맥 임베딩으로 이동했다.
TF-IDF/BoW + 선형분류(개념 요약)
- BoW/TF-IDF로 문서를 벡터화: \mathbf{x}\in\mathbb{R}^p (희소)
- 선형 분류기(로지스틱 회귀, 선형 SVM 등): \(z = \mathbf{w}^{\top}\mathbf{x} + b,p = \sigma(z)\)(이진) 또는 다중분류 softmax를 사용한다.
장점은 빠르고 강력한 베이스라인, 데이터가 적어도 안정적인 반면, 한계로는 단어 순서/문맥 정보 손실(동음이의, 긴 의존관계 처리 약함)이다.
Transformer 기반 문서 분류 파이프라인
Transformer(예: BERT류)는 토큰 시퀀스 (w_1,\dots,w_T)를 문맥 임베딩으로 바꾼다. \(\mathbf{H} = Transformer(w_{1:T})\)
대표적으로 [CLS] 토큰 표현 \mathbf{h}_{\text{CLS}} 또는 평균 풀링을 사용해 문서 벡터를 만들고, \(\mathbf{z} = W\mathbf{h}_{\text{CLS}} + b,\mathbf{p} = softmax(\mathbf{z})\)로 분류한다.
실무 파이프라인은 대개 토크나이즈 → 사전학습 Transformer 로딩, head 부착 → (동결 후 head 학습) → 점진적 fine-tuning, 불균형이면 class weight / 샘플링, 운영 전 calibration/threshold 튜닝으로 정리된다.
불균형/임계값/보정의 적용 포인트
문서 분류(특히 멀티라벨, 희귀 라벨)에서는 ”학습 성능”보다 ”운영 품질”이 더 중요해지는 경우가 많다.
- 불균형: 희귀 라벨 Recall이 급락 → class weight, focal, 라벨별 임계값 \(t_{k}\) 고려
- 임계값: 멀티라벨이면 \({\widehat{y}}_{k} = \mathbf{1}\{ p_{k} \geq t_{k}\}\)이며 global t보다 라벨별 t_k가 실무적으로 유리한 경우가 많다.
- 보정(calibration): Transformer도 과신이 흔하므로 calibration curve/ECE 확인 후 temperature scaling 적용, 그리고 보정된 확률로 임계값 재튜닝까지 한 세트로 운영하는 것이 안정적이다.
6. 평가와 임계값: 운영 관점의 의사결정 설계
딥러닝 분류 모델은 보통 확률 \(p(x) = P(Y = 1 \mid x)\) 또는 다중분류 확률벡터 \(\{ p_{k}(x)\}\)를 출력한다. 그러나 운영(실제 의사결정) 은 ”확률을 어떻게 행동(action)으로 바꿀 것인가”가 핵심이며, 그 연결고리가 임계값(threshold) 과 결정규칙(decision rule) 이다.
같은 모델이라도 임계값을 어떻게 두느냐에 따라 미탐/오경보/검토량/비용이 크게 달라진다. 따라서 분류 문제의 완성은 ”학습(확률 추정)“이 아니라, 평가 지표 + 운영 제약 + 임계값 정책까지 포함한 end-to-end 설계로 이해해야 한다.
확률 예측과 의사결정의 분리: 왜 임계값이 필요한가?
이진분류에서 모델은 확률 p(x)를 내지만, 실제 행동은 보통 임계값 t로 이산화된다. \(\widehat{y}(x) = \mathbf{1}\{ p(x) \geq t\}\)
여기서 중요한 분리는 다음과 같다.
- 학습(모형 추정): 손실(NLL/CE)을 최소화해 p(x)를 ”잘” 추정한다.
- 운영(정책 결정): 비용/제약/리소스에 맞춰 t 또는 정책을 선택한다.
즉 ”확률을 잘 맞추는 문제”와 ”그 확률로 최적 행동을 고르는 문제”는 서로 다른 최적화 문제다. 임계값은 이 둘을 연결하는 운영 레버다.
Confusion Matrix와 운영 지표: Precision/Recall/FPR/FNR
이진분류에서 혼동행렬은 네 가지로 요약된다: (1) TP: 실제 양성(1)을 양성으로 예측 (2) FP: 실제 음성(0)을 양성으로 예측(오경보) (3) FN: 실제 양성(1)을 음성으로 예측(미탐) (4) TN: 실제 음성(0)을 음성으로 예측.
이로부터 운영에서 자주 쓰는 지표가 정의된다.
- \(Precision = \frac{TP}{TP + FP}\text{(양성이라 예측한 것의 품질)}\)
- \(Recall = TPR = \frac{TP}{TP + FN}\text{(진짜 양성 중 얼마나 잡았나)}\)
- \(Specificity = \frac{TN}{TN + FP}\text{(진짜 음성 중 얼마나 음성이라 했나)}\)
- \(FPR = \frac{FP}{FP + TN} = 1 - SpecificityFNR = \frac{FN}{TP + FN} = 1 - Recall\)
임계값 t를 올리면 대체로 FP가 줄어 Precision은 오르기 쉽지만 Recall은 떨어진다. t를 내리면 그 반대가 된다. 이 trade-off 가 운영 의사결정의 핵심이다.
ROC–AUC: ”순위 분리력” 평가와 한계
임계값 t를 변화시키며 x축은 \(FPR(t)\), y축은 \(TPR(t) = Recall(t)\)를 그린 것이 ROC 곡선이다. AUC는 ROC 곡선 아래 면적이며, 다음과 같이 해석할 수 있다.
AUC는 ”무작위 양성 샘플이 무작위 음성 샘플보다 더 높은 점수를 받을 확률”이다.
즉 AUC는 순위 기반 분리력을 본다. 따라서 클래스 비율이 변해도 상대적으로 덜 흔들리는 장점이 있다.
다만 운영에서 중요한 ”양성 경보의 품질(Precision)“은 ROC에 직접 드러나지 않는다. 불균형(양성 희귀)에서는 ROC가 좋아 보여도 실제로는 FP가 대량 발생할 수 있으므로, 운영 관점에서는 ROC만으로 결정을 내리기 어렵다.
불균형에서 핵심: Precision–Recall(PR) 곡선과 AP
양성이 희귀한 문제(사기, 결함, 이상탐지, 의료 선별)에서는 ”Recall을 조금 올리려다가 FP가 폭증”하는 구간이 흔하다. 이때 ROC보다 더 직접적인 그림이 PR 곡선이다. x축은 \(Recall(t)\), y축은 \(Precision(t)\)이므러”얼마나 잡을 것인가(Recall)“와 ”잡은 것의 품질이 어떤가(Precision)”를 직접 연결해준다.
PR 곡선 아래 면적(정확히는 Precision의 Recall-가중 평균)을 AP(Average Precision) 라 한다. AP는 불균형 문제에서 모델 비교에 자주 사용되며, 특히 운영이 ”상위 경보를 사람/시스템이 검토”하는 형태일 때 더 실용적이다.
임계값 선택 1: 비용 기반 최적 임계값 \(t^{*}\)
운영에서 오경보 비용을 \(c_{FP}\), 미탐 비용을 \(c_{FN}\)이라 하자(정답 비용은 0으로 두는 단순화). 확률 \(p = P(Y = 1 \mid x)\)가 주어졌을 때,
- \(\widehat{y} = 1\)로 결정하면 기대비용: \(\mathbb{E}\lbrack C \mid \widehat{y} = 1\rbrack = c_{FP} \cdot P(Y = 0 \mid x) = c_{FP}(1 - p)\)
- \(\widehat{y} = 0\)로 결정하면 기대비용: \(\mathbb{E}\lbrack C \mid \widehat{y} = 0\rbrack = c_{FN} \cdot P(Y = 1 \mid x) = c_{FN}p\)
따라서 \(\widehat{y} = 1\)이 유리한 조건은 \(c_{FP}(1 - p) \leq c_{FN}p \leftrightarrow p \geq \frac{c_{FP}}{c_{FP} + c_{FN}}\)이다.
즉 비용 기반 최적 임계값은 \(t^{*} = \frac{c_{FP}}{c_{FP} + c_{FN}}\)으로 정리된다.
미탐 비용 \(c_{FN}\)이 크면 \(t^{*}\)는 내려가며(더 쉽게 양성), 오경보 비용 \(c_{FP}\)이 크면 \(t^{*}\)는 올라간다(더 보수적으로 양성).
임계값 선택 2: 제약 기반 선택(FPR 제한, 검토량 K 제한 등)
현장에서는 비용 숫자를 정확히 박기 어렵거나(정책/규제/리소스가 먼저인 경우) 제약 조건이 우선인 경우가 많다. 이때는 검증셋에서 제약을 만족하는 임계값을 찾는다.
FPR 제약: \(\mathrm{FPR}(t)\\le \\alpha\)
”오경보율은 1% 이하가 필수” 같은 규정이 있을 때, 여러 임계값 후보에 대해 \(\mathrm{FPR}(t)\) 를 계산하고 \(FPR(t) \leq \alpha\) 를 만족하는 영역에서 목표(Recall 최대, 비용 최소 등)를 최적화한다.
검토량(알림 수) 제약: ”하루 최대 K건만 검토 가능”
사기 의심 거래 상위 K건만 조사하는 경우처럼, 임계값 대신 Top-K 정책이 자연스럽다. 점수 s(x) 또는 확률 p(x)를 내림차순으로 정렬해 상위 K개만 양성(검토 대상으로) 처리한다.
이 관점에서는 ”임계값”이 고정값이 아니라, 그날의 데이터 분포에 따라 달라지는 동적 임계값으로 구현된다.
복합 제약
실무는 보통 제약이 하나가 아니다. 예를 들어 \(FPR(t) \leq \alpha\text{AND검토량} \leq K\)처럼 다중 제약을 동시에 만족시키는 영역에서, Recall 최대/Precision 최대/비용 최소 같은 목표를 최적화해 임계값을 결정한다.
불균형 학습과 임계값: ”학습을 바꾸면 임계값도 바뀐다”
불균형 대응(class weight, oversampling, focal loss, hard mining 등)을 적용하면 모델의 점수/확률 분포가 바뀐다. 그 결과 ”순위”는 좋아질 수 있어도 확률의 해석(정규화/보정)이 변형될 수 있고, 운영 임계값 t는 대개 다시 설계해야 한다.
따라서 불균형 문제는 ”학습 기법”만으로 끝나지 않고, PR 관점 평가 + 임계값 정책까지 포함한 최적화로 완성된다.
운영 관점 체크리스트: 무엇을 먼저 결정할까?
운영 설계는 다음 순서가 실무적으로 안정적이다.
1. 운영 목표 명시: 미탐이 더 치명적인가, 오경보가 더 치명적인가? 검토량 제한이 있는가?
2. 평가 지표 선택: 일반 분류: ROC/AUC + 정확도 지표, 불균형/검출: PR/AP, Recall@K(또는 Precision@K) 중심
3. 임계값 정책 선택: 비용이 명확하면 \(t^{*} = \frac{c_{FP}}{c_{FP} + c_{FN}}\), 제약이 우선이면 \(FPR \leq \alpha\), 검토량 \(\leq K\), Top-K 정책
4. 검증셋에서 튜닝: 선택한 정책이 실제로 목표/제약을 만족하는지 확인
5. (필요 시) 보정 후 재튜닝: calibration을 수행하면 확률이 바뀌므로 t도 다시 맞춘다.
7. Calibration & Uncertainty: 과신을 줄이고 안정적 의사결정을 만드는 법
앞 절에서 보았듯이, 운영의 핵심은 ”확률을 행동으로 바꾸는 규칙(임계값/정책)“이다. 그런데 이 규칙이 의미를 가지려면, 모델이 내놓는 확률이 단지 ”점수”가 아니라 신뢰 가능한 확률이어야 한다.
딥러닝 분류는 정확도는 높지만 확률이 지나치게 확신적인 경우가 흔하고, 분포 이동(OOD), 불균형, noisy label 환경에서는 그 문제가 더욱 두드러진다.
이 절에서는 (1) calibration이 무엇이며 왜 필요한지, (2) calibration을 어떻게 평가하는지, (3) 대표 보정 방법(temperature/Platt/isotonic), (4) uncertainty를 이용한 안정적 의사결정(거절/검토/리스크 관리)까지 하나의 운영 파이프라인으로 정리한다.
Calibration이란 무엇인가: ”0.8이라 말한 것 중 80%가 맞는가?”
이진분류에서 모델이 \(\widehat{p}(x) = 0.8\)이라고 출력한 샘플들을 모았을 때, 그 집합에서 실제 양성 비율이 약 0.8이라면 그 모델은 calibrated 라고 말한다.
즉 calibration은 ”순위(누가 더 위험한가)“가 아니라, 확률의 의미가 현실과 맞는가를 묻는다.
- 좋은 분리력(discrimination): 위험한 샘플이 더 높은 점수를 받는가? (AUC/PR 등)
- 좋은 보정(calibration): 점수 자체가 확률로 해석 가능한가? (reliability/ECE/Brier 등)
운영에서 비용 기반 임계값 \(t^{*} = \frac{c_{FP}}{c_{FP} + c_{FN}}\)같은 규칙이 ”정당”해지려면, \(\widehat{p}(x)\)가 확률로서 해석 가능해야 한다. 즉 calibration은 단순한 평가 지표가 아니라 정책 설계의 기반이다.
과신이 생기는 구조적 이유(요약)
딥러닝 분류가 과신하기 쉬운 이유는 보통 단일 원인이 아니라 구조와 데이터/학습 환경이 결합된 결과다.
softmax 경쟁 구조: 다중분류에서 \(\sum_{k}p_{k} = 1\)이 강제되므로 ”모르는 입력”에도 확률 질량을 반드시 배분한다. OOD에서 \(\max_{k}p_{k}\)가 커지는 현상이 흔한 이유다.
cross-entropy의 압력: CE는 정답 확률 \(p_{y}\)를 1로 밀어붙인다: \(\mathcal{L} = - \log p_{y}\). 데이터가 쉽게 분리되거나 모델 용량이 크면 로짓 스케일이 커져 확률이 극단화될 수 있다.
데이터 편향/라벨 노이즈/분포 이동: 훈련 분포가 운영 분포를 충분히 대표하지 못하면(표본 편향), 모델은 ”보지 못한 영역”에서도 높은 확률을 낼 수 있다. 라벨 노이즈가 있어도 CE는 틀린 라벨을 맞추려는 방향으로 강하게 학습되어 불필요한 확신이 쌓일 수 있다.
Calibration 평가: Reliability diagram / ECE / Brier score
Reliability diagram(= calibration curve): 예측확률 \({\widehat{p}}_{i}\)를 구간(bin)으로 나눈 뒤, 각 구간에서 평균 예측확률(신뢰도) \(conf(b)\)와 실제 정답 비율(정확도) \(acc(b)\)을 비교한다.
이진분류 예시: \(acc(b) = \frac{1}{|B_{b}|}\sum_{i \in B_{b}}y_{i},conf(b) = \frac{1}{|B_{b}|}\sum_{i \in B_{b}}{\widehat{p}}_{i}\)
완전 보정이면 \(acc(b) \approx conf(b)\)가 되어 대각선 근처에 놓인다. 만약 과신이면 \(conf(b) > acc(b)\), 과소신이면 \(conf(b) < acc(b)\)
ECE(Expected Calibration Error): ECE는 구간별 불일치의 가중 평균이다. \(ECE = \overset{B}{\sum_{b = 1}}\frac{|B_{b}|}{n}\left| acc(b) - conf(b) \right|\)
작을수록 보정이 잘 된 것이다. 단, bin 개수 B와 binning 방식에 민감할 수 있으므로 평가 세팅을 명시하는 것이 좋다.
Brier score(확률 예측의 제곱오차): Brier score는 calibration과 sharpness(확률 분포의 분별력)를 함께 반영하는 확률 오차다.
- 이진분류: \(BS = \frac{1}{n}\overset{n}{\sum_{i = 1}}({\widehat{p}}_{i} - y_{i})^{2}\)
- 다중분류(원-핫 \(y_{ik}\), 확률 \(p_{ik}\)): \(BS = \frac{1}{n}\overset{n}{\sum_{i = 1}}\overset{K}{\sum_{k = 1}}(p_{ik} - y_{ik})^{2}\)
Calibration 방법: 모델은 고정하고 ”출력 변환”을 학습한다
실무에서 보정은 ”모델을 다시 학습”하기보다, 학습된 모델의 로짓/점수(score) 를 사후 변환해 확률을 조정하는 방식이 안정적이다. 핵심은 검증셋(또는 별도의 calibration set) 에서 변환 파라미터를 추정하는 것이다.
Temperature scaling(softmax 로짓 보정): 다중분류에서 로짓 \(\mathbf{z}\)에 온도 T>0를 적용해 \(\mathbf{p}^{(T)} = softmax(\frac{\mathbf{z}}{T})\)로 확률을 재계산한다.
\(T > 1\): 분포를 평평하게 만들어 과신 완화(가장 흔한 케이스)
\(T < 1\): 분포를 더 뾰족하게(과소신 보정일 때)
T는 calibration set에서 NLL(=CE)을 최소화하도록 추정한다.
\(T^{*} = \arg\min_{T}\overset{n}{\sum_{i = 1}}( - \log p_{i,y_{i}}^{(T)})\). 장점은 분류 순위(Top-1)는 거의 유지되면서 확률만 조정되고 운영 임계값 설계가 쉬워진다는 것이다.
Platt scaling(주로 이진분류: \(score \rightarrow sigmoid\)): 어떤 점수 s(x)에 대해 \(\widehat{p}(x) = \sigma(as(x) + b)\) 형태로 a,b를 calibration set에서 추정한다(SVM에서 유래했지만 딥러닝 로짓에도 적용 가능). 파라미터 수가 적고 데이터가 많지 않아도 비교적 안정적이다.
Isotonic regression(비모수 단조 보정): 확률을 단조 함수 g(\cdot)로 보정한다. \(\widehat{p}(x) = g(s(x))\). 장점으로 함수 형태 가정이 약해 유연하다는 것이고, 데이터가 적으면 과적합 위험이 있고, 특히 희귀 양성에서 불안정할 수 있다는 단점이 있다.
데이터가 충분하면 isotonic을 고려할 수 있고, 그렇지 않으면 temperature/Platt처럼 파라미터가 적은 방법이 안전한 편이다.
Uncertainty(불확실성): ”확률이 높다/낮다”와는 다른 축
보정(calibration)은 ”출력 확률이 의미를 갖는가”를 다루고, 불확실성은 ”이 예측을 얼마나 믿어도 되는가”를 다룬다. 운영에서는 둘이 결합되어 안정적 의사결정을 만든다.
불확실성은 보통 두 종류로 나눠 설명한다.
- Aleatoric uncertainty(데이터 고유의 불확실성): 입력 자체가 애매하거나 노이즈가 큰 경우(본질적으로 구분이 어려움)
- Epistemic uncertainty(모델 불확실성): 데이터 부족/분포 밖 입력/OOD 등으로 모델이 ”모르는” 영역
실무적으로는 이론적 분해보다, 다음과 같은 운영 질문으로 연결하는 것이 중요하다. ”이 샘플은 자동처리해도 되는가?“, ”사람 검토로 보내야 하는가?”, ”거절/보류(unknown)해야 하는가?”
안정적 의사결정 설계: Reject/Review/Defer 정책
불확실성을 운영으로 연결하는 가장 실용적인 방법은 ”3갈래 정책”이다. (1) Auto-accept / Auto-reject: 확신이 충분히 높을 때 자동 결정, (2) Review(사람 검토): 확률이 애매하거나 리스크가 큰 구간, (3) Reject/Defer(unknown/보류): OOD 가능성이 높거나 모델이 모르는 영역이다.
단순 임계값 + 회색지대(gray zone)
이진분류에서 \(\widehat{p}(x) \geq t_{\text{high}}\)이면 자동 양성, \(\widehat{p}(x) \leq t_{\text{low}}\)이면 자동 음성, 그 사이는 검토로 보낸다.
즉, \(\text{review if}t_{\text{low}} < \widehat{p}(x) < t_{\text{high}}\). 이는 ”정책을 한 번 더” 얹는 방식이며, 검토량(리소스) 제약과 잘 맞는다.
OOD/unknown 거절(거리 기반 또는 최대확률 기반)
softmax 기반에서는 \max_k p_k가 작으면 ”잘 모른다”는 신호로 쓰기도 한다(단, OOD에서 과신이 가능하므로 calibration과 함께 써야 한다).
metric learning/embedding 기반이라면 거절 규칙이 더 자연스럽다. \(\min_{k}d(\mathbf{h},\mathbf{c}_{k}) > \tau \Rightarrow \text{unknown}\). 즉 ”가까운 클래스가 없다”는 신호로 reject가 가능하다.
Large-K에서의 연결: Top-k 의사결정과 확률 품질
Large-K 추천/검색에서는 전체 확률분포가 꼭 필요하지 않고 Top-k 품질이 핵심인 경우가 많다. 이때는 Stage 1: retrieval(임베딩 + ANN)로 후보 회수, Stage 2: rerank로 정밀 점수화를 사용하며, ”확률이 필요한 구간”은 보통 Stage 2 후보 집합 내부에서만 의미를 가진다.
즉 실무에서는 전체 K에 대해 잘 보정된 확률이 필요한가?, 아니면 후보 내부에서의 점수/확률만 충분한가?를 먼저 결정해야 하며, 필요 시 후보 집합 \mathcal{C}_N(x)에 대해 조건부 softmax로 확률화하고 temperature scaling으로 보정하는 방식이 쓰인다.
Calibration 운영 체크리스트(실전 4단계)
1. 진단: reliability diagram으로 과신/과소신 구간을 먼저 확인
2. 수치화: ECE/Brier를 기록해 모델/버전 간 비교 가능하게 함
3. 보정: temperature scaling(기본), 필요 시 Platt/isotonic 적용
4. 정책 재튜닝: 보정 후 확률이 바뀌므로 임계값/Top-k/검토량 규칙을 다시 맞춤