MLDL 예측방법 | 차원축소

Chapter 1. 차원축소방법

1. 차원축소 개념

지금까지 논의한 방법들은 두 가지 서로 다른 방식으로 분산을 제어했다. 하나는 원래 변수들의 부분집합(subset) 만을 사용하는 방식이고, 다른 하나는 계수들을 0 쪽으로 수축(shrinkage) 시키는 방식이다. 이 방법들은 모두 원래 예측변수 \(X_{1},X_{2},\ldots,X_{p}\)를 그대로 사용하여 정의된다. 이제는 예측변수들을 변환 한 뒤, 변환된 변수들을 사용해 최소제곱 모형을 적합하는 접근을 살펴본다. 이러한 기법들을 차원축소 방법 이라고 부른다.

\(Z_{1},Z_{2},\ldots,Z_{M}\)이 원래 p개 예측변수의 선형결합으로 이루어진, \(M < p\)개의 변수라고 하자. 즉, \(Z_{m} = \overset{p}{\sum_{j = 1}}\phi_{jm}X_{j}\)이며, 어떤 상수 \(\phi_{1m},\phi_{2m},\ldots,\phi_{pm}\)에 대해 \(m = 1,\ldots,M\)이다. 그러면 다음 선형회귀모형을 최소제곱으로 적합할 수 있다.

\(y_{i} = \theta_{0} + \overset{M}{\sum_{m = 1}}\theta_{m}z_{im} + \varepsilon_{i},i = 1,\ldots,n\), 여기서 \(\theta_{0},\theta_{1},\ldots,\theta_{M}\)회귀계수이다. 만약 \(\phi_{1m},\ldots,\phi_{pm}\)들이 잘 선택된다면, 이러한 차원축소 접근은 종종 최소제곱 회귀를 능가할 수 있다.

”차원축소”라는 말은, p+1개의 계수 \(\beta_{0},\beta_{1},\ldots,\beta_{p}\)를 추정하는 문제를, M+1개의 계수 \(\theta_{0},\theta_{1},\ldots,\theta_{M}\)를 추정하는 더 단순한 문제로 바꾼다는 데서 온다(\(M < p\)). 즉, 문제의 차원(dimension)이 p+1에서 M+1로 줄어든 것이다.

\(\overset{M}{\sum_{m = 1}}\theta_{m}z_{im} = \overset{M}{\sum_{m = 1}}\theta_{m}\overset{p}{\sum_{j = 1}}\phi_{jm}x_{ij} = \overset{p}{\sum_{j = 1}}\overset{M}{\sum_{m = 1}}\theta_{m}\phi_{jm}x_{ij} = \overset{p}{\sum_{j = 1}}\beta_{j}x_{ij}\), 여기서 \(\beta_{j} = \overset{M}{\sum_{m = 1}}\theta_{m}\phi_{jm}\)이다. 따라서 원래 선형회귀모형의 특수한 경우로 생각할 수 있다. 차원축소는 \(\beta_{j}\)의 형태를 위와 같이 제한하므로, 추정된 \(\beta_{j}\) 계수에 제약을 가한다. 이 제약은 계수 추정치에 편향을 유발할 수 있다. 그러나 p가 n에 비해 큰 상황에서는, \(M \ll p\)를 선택함으로써 적합된 계수들의 분산을 크게 줄일 수 있다.

만약 M=p이고 모든 \(Z_{m}\)이 선형독립이면, 위의 식은 아무 제약도 주지 않는다. 이 경우에는 차원축소가 일어나지 않으며, 원래 p개 예측변수로 최소제곱을 수행하는 것과 동치이다.

모든 차원축소 방법은 두 단계로 작동한다. (1) 변환된 예측변수 \(Z_{1},\ldots,Z_{M}\)을 얻고, (2) 이 M개 예측변수를 사용해 모형을 적합한다. 다만 \(Z_{1},\ldots,Z_{M}\) (또는 \(\phi_{jm}\))를 선택하는 방식은 여러 가지가 있을 수 있다. 여기서는 주성분(principal components) 과 부분최소제곱(partial least squares), 두 가지 접근을 다룬다..

2. Principal Components Regression (주성분 회귀, PCR)

회귀를 위한 차원축소로서의 PCA

주성분분석(PCA)은 다수의 변수를 몇 개의 대표적인 축(주성분)으로 요약해, 저차원의 특징 집합을 만들어내는 데 널리 쓰이는 방법이다. PCA는 반응변수 Y를 사용하지 않고 입력 X의 구조(변동이 큰 방향)를 먼저 파악한다는 점에서 비지도학습(unsupervised learning) 도구로 자주 활용된다. 다만 PCA는 탐색적 분석에만 머무는 기법이 아니라, 생성된 주성분들을 설명변수로 삼아 회귀모형을 구성함으로써 차원축소 기반 예측에도 직접 연결될 수 있다. 따라서 여기서는 PCA를 ”데이터 요약 기법”으로만 소개하는 것이 아니라, 회귀를 위한 차원축소(PCR로의 연결) 관점에서 유연하게 설명한다.

주성분분석의 개요

PCA는 \(n \times p\) 데이터 행렬 X의 차원을 줄이는 기법이다. 데이터의 첫 번째 주성분 방향(first principal component direction) 은 관측치들이 가장 크게 변동하는 방향이다. 초록 실선은 데이터의 첫 번째 주성분 방향이다. 눈으로 보아도 이 방향이 데이터 변동이 가장 큰 방향임을 알 수 있다. 이 직선으로 관측치를 사영(projection)하면 사영된 값들의 분산이 가능한 한 최대가 된다. 다른 어떤 직선에 사영하더라도 더 작은 분산을 얻게 된다.

\(Z_{1} = 0.839 \times (X_{1} - \overline{X_{1}}) + 0.544 \times (X_{2} - \overline{X_{2}})\), 여기서 \(\phi_{11} = 0.839,\phi_{21} = 0.544\)는 주성분 적재치(loadings) 이며 앞서 말한 방향을 정의한다.\(\phi_{11}^{2} + \phi_{21}^{2} = 1\)을 만족하는 모든 가능한 선형결합 중에서, 이 선형결합이 \(Var(\phi_{11}(X_{1} - \overline{X_{1}}) + \phi_{21}(\phi_{11}(X_{2} - \overline{X_{2}})\)을 최대화한다는 점이다. \(\phi_{11}^{2} + \phi_{21}^{2} = 1\)형태만 고려해야 하는 이유는, 그렇지 않으면 \(\phi_{11},\phi_{21}\)이 무수히 많이 존재한다.

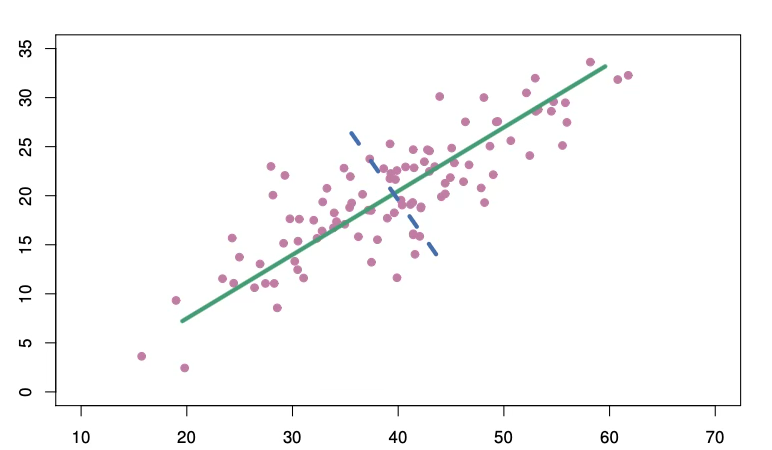
첫 번째 주성분 벡터는 데이터에 가장 가깝게 놓이는 직선을 정의한다. 예컨대 첫 번째 주성분 직선은 각 점에서 그 직선까지의 수직거리의 제곱합을 최소화한다. 주성분 \(Z_{1}\)의 값은 각 지역의 (pop, ad) 정보를 한 숫자로 요약한 것으로 볼 수 있다.

두 번째 주성분 \(Z_{2}\)는 \(Z_{1}\)과 상관이 0이면서, 그 제약 하에서 분산이 최대인 선형결합이다. 두 번째 주성분 방향은 위의 그림에서 파란 점선으로 표시된다. \(Z_{1}\)과 \(Z_{2}\)의 상관이 0이라는 조건은, 두 번째 방향이 첫 번째 주성분 방향에 직교(orthogonal) 한다는 조건과 동치이다. 두 번째 주성분은 \(Z_{1} = 0.544 \times (X_{1} - \overline{X_{1}}) - 0.839 \times (X_{2} - \overline{X_{2}})\)로 주어진다. 예측변수가 두 개인 구성상 첫 번째 주성분이 더 많은 정보를 담는다. p차원 데이터에서는 최대 p의 주성분을 만들 수 있다.

주성분 회귀(PCR) 접근

주성분 회귀(PCR)는 첫 M개의 주성분 \(Z_{1},\ldots,Z_{M}\)을 만든 뒤, 이 성분들을 예측변수로 사용해 최소제곱 선형모형을 적합한다. 핵심 아이디어는, 종종 소수의 주성분만으로도 예측변수들의 변동 대부분과(그리고) 반응변수와의 관계를 설명할 수 있다는 점이다. 다시 말해 \(X_{1},\ldots,X_{p}\)가 가장 크게 변동하는 방향들이 Y와 관련된 방향이라고 가정한다. 이 가정이 항상 참인 것은 아니지만, 실제로는 꽤 그럴듯한 근사로서 좋은 결과를 주는 경우가 많다.

PCR의 핵심 가정—즉, 설명변수 \(X_{1},\ldots,X_{p}\)가 크게 변동하는 방향이 반응변수 Y 예측에도 중요하다—이 성립한다면, 원래 변수 X에 대해 최소제곱을 적합하는 것보다 상위 M개 주성분 \(Z_{1},\ldots,Z_{M}\)에 대해 최소제곱을 적합하는 편이 더 좋은 예측 성능을 낳을 수 있다. 이는 Y와 관련된 정보가 상위 주성분들에 주로 압축되어 있고, M<p개의 계수만 추정함으로써 모형 복잡도를 낮춰 과적합을 완화할 수 있기 때문이다. 특히 첫 번째 주성분이 설명변수들의 분산 대부분을 설명하는 상황이라면, Z_1 하나만으로 반응을 예측하는 PCR도 충분히 잘 작동할 가능성이 크다. 더 나아가 주성분들은 서로 직교(상관 0) 하도록 구성되므로, 원래 변수들에서 흔히 문제가 되는 다중공선성이 구조적으로 발생하지 않는다는 장점도 갖는다.

PCR을 수행할 때는 일반적으로 각 예측변수를 표준화한 뒤 주성분을 생성할 것을 권한다. 이는 모든 변수를 같은 스케일에 놓아준다. 표준화가 없으면 분산이 큰 변수들이 주성분에 더 크게 반영되고, 변수의 측정 단위가 최종 PCR 모형에 영향을 주게 된다. 다만 모든 변수가 같은 단위(예: kg, inch)로 측정되었다면 표준화를 하지 않기로 선택할 수도 있다.

3. Partial Least Squares (부분최소제곱, PLS)

앞서 설명한 PCR은 \(X_{1},\ldots,X_{p}\)예측변수들을 가장 잘 대표하는 선형결합(방향)을 찾는 것이다. 이 방향들은 반응 Y를 사용하지 않는 비지도(unsupervised) 방식으로 식별된다. 즉 반응이 주성분 방향 선택을 ”감독(supervise)“하지 않는다. PCR은 X의 분산이 큰 방향을 기준으로 주성분을 만들기 때문에, 반응변수 Y 의 정보가 주성분 구성에 직접 반영되지 않는다. 이에 대한 감독적(supervised) 대안으로 부분최소제곱(Partial Least Squares, PLS)이다.

PLS 역시 차원축소 방법이며, 먼저 원래 예측변수들의 선형결합으로 새로운 특징 \(Z_{1},\ldots,Z_{M}(M < p)\)을 구성한 뒤, 이 M개의 특징으로 최소제곱 선형모형을 적합한다. 그러나 PCR과 달리 PLS는 \(Z_{m}\)을 만들 때 Y를 함께 사용하여, 예측변수들을 잘 요약할 뿐 아니라 반응과도 강하게 관련된 방향을 우선적으로 찾는다. 즉 PLS는 대략적으로 ”X의 변동을 설명하면서 동시에 Y 예측에 유리한” 축을 구성하려는 방법이다.

첫 번째 PLS 성분의 구성(직관적 정의)

예측변수들을 평균 0으로 중심화(보통 표준화까지)한 뒤, 첫 번째 PLS 성분은 \(Z_{1} = \overset{p}{\sum_{j = 1}}\phi_{j1}X_{j}\)처럼 정의된다. 이때 가중치 \(\phi_{j1}\)는 각 \(X_{j}\)가 Y와 얼마나 강하게 연관되는지를 반영하도록 정해진다. 직관적으로는 \(\phi_{j1}\)을 Y를 \(X_{j}\)에 대해 단순선형회귀한 기울기 계수로 둘 수 있으며, 예측변수를 표준화한 경우 이 기울기는 Y와 \(X_{j}\)의 상관(correlation)에 비례한다. 따라서 \(Z_{1}\)을 계산할 때 PLS는 반응 Y와 더 강하게 관련된 예측변수에 더 큰 가중치를 부여하게 된다.

두 번째 PLS 성분의 구성(잔차화/직교화 아이디어)

첫 번째 성분 \(Z_{1}\)은 Y와 관련이 큰 방향을 반영하도록 구성되지만, \(Z_{2}\)는 \(Z_{1}\)과 동일한 정보를 반복해서 담지 않도록 이미 \(Z_{1}\)이 설명한 부분을 제거한 뒤 남은 변동에서 다시 Y와 관련된 방향을 찾는다. 이를 위해 PLS는 다음과 같은 ”잔차화(residualization)” 절차를 사용한다.

1. 먼저 \(Z_{1}\)을 계산한다. \(Z_{1} = \overset{p}{\sum_{j = 1}}\phi_{j1}X_{j}\).

2. 각 예측변수 \(X_{j}\)를 \(Z_{1}\)에 대해 단순선형회귀하여, \(Z_{1}\)로 설명되는 성분을 제거한 잔차(residual) 를 만든다. \(X_{j} = a_{j1}Z_{1} + r_{j1},j = 1,\ldots,p\)

여기서 \(r_{j1}\)는 \(Z_{1}\)과 직교(상관 0)인 ”남은 부분”이며, Z_1이 설명하지 못한 정보가 담겨 있다.

3. 이제 원래의 \(X_{j}\)대신 잔차 \(r_{j1}\)들을 새로운 입력으로 보고, 1번과 같은 원리로 두 번째 성분을 구성한다. \(Z_{2} = \overset{p}{\sum_{j = 1}}\phi_{j2}r_{j1}\). 이때 가중치 \(\phi_{j2}\)는 Y와의 관련성을 반영하도록 정해지므로, 결과적으로 \(Z_{2}\)는 ”\(Z_{1}\)이 제거된 이후에도 남아 있는 Y-관련 신호”를 최대한 담는 방향이 된다.

4. 같은 절차를 반복하여 \(Z_{3},\ldots,Z_{M}\)을 순차적으로 만들고, 최종적으로는 \(Z_{1},\ldots,Z_{M}\)을 예측변수로 사용해 Y에 대한 최소제곱 선형모형을 적합한다. \(Y = \theta_{0} + \theta_{1}Z_{1} + \cdots + \theta_{M}Z_{M} + \varepsilon\).

요약하면, PLS의 \(Z_{2}\)는 단순히 ”두 번째로 큰 분산 방향”이 아니라, 첫 번째 성분 \(Z_{1}\)이 이미 담은 정보를 제거한 뒤에도 남아 있는 변동 중에서 Y 예측에 유리한 방향을 다시 찾아 만든 성분이다. 이 점이 Y를 사용하지 않는 PCR과 구별되는 핵심이다.

성분개수 \(M\) 결정

또한 PLS에서 사용할 성분 개수 M은 모형의 유연성을 조절하는 튜닝 파라미터이다. M이 커질수록 편향은 줄어들 수 있으나 분산이 증가하여 과적합 위험이 커질 수 있으므로, M은 보통 교차검증(cross-validation) 으로 선택하는 것이 표준이다. PLS는 Y를 활용해 성분을 구성하므로 PCR보다 반응과의 관련 정보를 더 직접적으로 반영할 수 있지만, 그만큼 데이터에 대한 적응이 강해져 분산이 늘어날 수 있다. 따라서 실제 성능에서 PLS가 항상 PCR이나 Ridge보다 우월하다고 말할 수는 없으며, 최종적으로는 검증오차(또는 테스트오차) 기반으로 비교·선택하는 것이 타당하다.

4. 고차원에서의 고려사항

High-Dimensional Data (고차원 데이터) 개념

전통적인 회귀·분류 기법 대부분은 관측치 수 n이 특징 수 p보다 훨씬 큰 저차원(low-dimensional) 설정을 전제로 한다. 이는 통계학 역사에서 다뤄온 많은 과학적 문제가 저차원 문제였기 때문이기도 하다. 예를 들어 환자의 혈압을 나이, 성별, BMI로 예측하는 문제를 생각해 보자. 예측변수는 3개(절편 포함 시 4개)이고, 수천 명 환자에 대해 자료가 있다면 \(n \gg p\)이므로 저차원 문제이다(여기서 차원은 p의 크기를 뜻한다).

하지만 지난 20년간 새로운 기술이 금융, 마케팅, 의학 등 다양한 분야의 데이터 수집 방식을 바꾸었다. 이제는 매우 많은 특징 측정값을 수집하는 것이 흔해졌다(p가 매우 큼). 반면 n은 비용, 표본 확보 등의 이유로 제한되는 경우가 많다. 예를 들면 다음과 같다.

1. 혈압을 나이/성별/BMI뿐 아니라 50만 개 SNP(단일염기다형성; 비교적 흔한 DNA 변이)까지 포함해 예측하려 할 수 있다. 이때 \(n \approx 200,p \approx 500,000\)이 될 수 있다.

2. 온라인 쇼핑 패턴을 이해하려는 마케팅 분석가는 검색엔진 사용자가 입력한 모든 검색어를 특징으로 사용할 수 있다(일명 ”bag-of-words” 모형). 그러나 정보 제공에 동의한 사용자 수는 수백~수천 명에 불과할 수 있다. 한 사용자에 대해 각 검색어는 존재/부재(0/1)로 기록되어 큰 이진 특징 벡터를 만든다. 이때 \(n \approx 1,000\)이고 p는 훨씬 더 커진다.

관측치보다 특징이 더 많은 데이터셋을 흔히 고차원이라고 한다. 이 설정에서 최소제곱 선형회귀 같은 고전적 방법은 적절하지 않다. 고차원 분석에서 생기는 많은 이슈는 n>p에서도 이미 논의한 바 있는데, 편향–분산 트레이드오프와 과적합 위험이 그것이다. 이런 이슈들은 항상 중요하지만, p가 n에 비해 매우 큰 경우 특히 더 중요해진다.

고차원에서 무엇이 잘못되는가?

p>n인 고차원 환경에서 회귀·분류를 수행할 때는, 저차원(\(n \gg p\))에서 통하던 직관과 평가 방식이 쉽게 무너진다. 이를 이해하기 위해, 고차원에 맞지 않은 고전적 기법을 그대로 적용하면 어떤 문제가 생기는지부터 살펴본다. 여기서는 최소제곱 회귀를 중심 예로 들지만, 같은 논리는 로지스틱 회귀나 선형판별분석(LDA) 같은 다른 고전적 방법에도 공통적으로 적용된다.

특징 수 p가 관측치 수 n만큼 크거나 더 크면, 최소제곱은 계산적으로 불안정해지거나(해가 유일하지 않음), 설령 계산되더라도 적용해서는 안 되는 경우가 많다. 이유는 단순하다. 실제로 반응 Y와 특징 X 사이에 의미 있는 관계가 존재하든 존재하지 않든, \(p \geq n\)이면 최소제곱은 훈련 데이터에서 잔차가 0이 되는 완벽한 적합을 만들어내는 계수 추정치를 쉽게 산출할 수 있기 때문이다. 즉, 훈련 데이터를 ”너무 잘” 맞추는 것이 가능해지고, 이때 얻어진 모형은 거의 필연적으로 과적합으로 이어진다.

이 현상은 저차원에서도 축소된 형태로 확인할 수 있다. 예를 들어 설명변수가 1개인 단순회귀에서도 관측치가 충분하면 회귀선은 데이터를 완벽히 관통하지 않고 전체 경향을 근사한다. 그러나 관측치 수가 극단적으로 적어지면, 직선은 주어진 점들을 정확히 통과하는 해를 가지게 된다. 이때 훈련 오차는 매우 작거나 0이 될 수 있지만, 이는 ”일반화가 잘 되었다”는 뜻이 아니라 표본에 특화된 우연한 패턴까지 흡수했다는 뜻이므로, 새로운 데이터에서는 성능이 급격히 악화될 가능성이 크다. 고차원에서는 이 문제가 훨씬 더 강하게 나타난다. 훈련 데이터를 완벽히 맞추는 것이 구조적으로 가능해지기 때문에, 최소제곱 모형은 지나치게 유연해져 독립 테스트셋에서 극도로 나쁜 성능을 보일 수 있다. 요약하면, p>n 또는 \(p \approx n\)에서는 단순한 최소제곱 적합이 과적합을 유발하기 쉬운 구조를 갖는다.

더 위험한 점은, 고차원에서는 ”훈련 데이터에서 좋아 보이는 지표”가 거의 항상 착시를 만든다는 것이다. 반응과 전혀 관련 없는 잡음 특징들을 계속 추가하더라도, 훈련 기준의 적합도는 단조롭게 좋아질 수 있다. 예컨대 변수를 늘릴수록 \(R^{2}\)는 1에 가까워지고 훈련 MSE는 0에 가까워지는 현상이 나타난다. 하지만 이는 실제 신호를 학습했다는 근거가 아니라, 자유도가 늘어나면서 우연한 변동까지 설명해버린 결과이다. 반면 독립 테스트셋에서의 MSE는 오히려 변수가 늘수록 커질 수 있는데, 이는 불필요한 변수가 증가할수록 계수 추정의 분산이 크게 증가하고, 그 불안정성이 예측오차로 직결되기 때문이다. 결국 테스트 성능 관점에서 최선의 모형은 소수의 변수(또는 강한 규제)를 사용하는 경우가 많지만, 훈련 \(R^{2}\)나 훈련 MSE만 보면 변수가 많을수록 좋아 보이므로 완전히 잘못된 결론에 도달하기 쉽다.

따라서 고차원에서는 훈련 적합도 지표(훈련 \(R^{2}\), 훈련 MSE 등)를 ”모형의 우수성” 근거로 삼는 것이 부적절하며, 반드시 교차검증이나 독립 테스트셋을 통해 일반화 성능을 평가해야 한다. 또한 모형의 유연성을 강제로 낮추는 규제(예: Ridge, Lasso)나 차원축소(PCR/PLS) 같은 고차원 친화적 기법이 필요해진다.

또한 저차원 설정에서는 변수 개수에 따른 과적합을 보정하기 위해, 훈련 RSS나 \(R^{2}\)를 그대로 쓰지 않고 모형 복잡도를 반영해 조정한 기준(예: AIC, BIC, 수정된 \(R^{2}\))을 사용해왔다. 그러나 고차원(\(p \geq n\))에서는 이러한 기준들이 전제하는 가정이 무너지기 때문에, 그대로 적용하는 것이 적절하지 않다.

핵심 문제는 오차분산 \({\widehat{\sigma}}^{2}\)의 추정이 성립하기 어렵다는 점이다. 많은 정보기준과 보정지표는 \({\widehat{\sigma}}^{2}\)를 기반으로 ”적합도–복잡도”의 균형을 계산하는데, p\ge n에서는 최소제곱이 훈련 데이터를 완벽히 맞추는 해를 만들 수 있어 훈련 잔차가 0이 되기 쉽다. 이 경우 고전적 분산추정식은 \({\widehat{\sigma}}^{2} = 0\) 같은 비현실적인 값을 산출할 수 있으며, 그 결과 AIC, BIC 등도 정상적으로 작동하지 않는다.

수정된 \(R^{2}\) 역시 유사한 한계를 가진다. 수정 \(R^{2}\)는 변수 수 증가에 따른 ”형식적 보정”을 포함하지만, 고차원에서는 훈련 데이터에서 잔차를 거의 0으로 만드는 모형이 쉽게 존재하므로, 수정 \(R^{2}\)가 1에 가까운(혹은 1인) 모형도 어렵지 않게 만들어진다. 즉, 고차원에서는 이러한 지표들이 과적합을 억제하는 역할을 충분히 수행하지 못하고, 오히려 잘못된 안정감을 줄 위험이 있다.

따라서 고차원에서는 훈련 기반 보정지표에 의존하기보다, 교차검증이나 독립 테스트셋 기반의 일반화 성능 평가를 중심으로 모델을 선택해야 하며, 동시에 Ridge/Lasso/Elastic Net 같은 규제 방법이나 PCR/PLS 같은 차원축소 방법처럼 고차원에 적합한 절차를 사용해야 한다.

5. 혼합형(측정형+범주형) 차원축소

현실의 데이터 분석에서는 연속형(측정형) 변수와 범주형 변수가 함께 존재하는 경우가 일반적이다. 그러나 지금까지 다룬 대표적인 차원축소 기법인 PCA는 연속형 변수만을 전제로 설계된 방법이다. 여기서는 범주형 변수가 포함된 상황에서 왜 기존 방법이 실패하는지, 그리고 이를 해결하기 위한 범주형 전용 및 혼합형 차원축소 방법을 체계적으로 정리한다.

(1) 범주형 변수는 왜 차원축소를 달리해야 하는가

범주형 변수는 연속형 변수와 근본적으로 다른 성질을 가진다.

첫째, 수치의 크기와 거리 개념이 존재하지 않는다. 범주형 변수에서 숫자는 단지 라벨일 뿐이며, 예를 들어 범주 1과 2의 차이가 범주 2와 3의 차이보다 ”작다”는 해석은 의미가 없다.

둘째, 분산(variance)의 개념이 부적절하다. PCA는 분산을 최대화하는 방향을 찾는 방법이지만, 범주형 변수에는 자연스러운 분산 개념이 정의되지 않는다.

셋째, 더미 변환 후 PCA 적용은 왜곡을 초래한다. 더미 변수는 0/1 값만 가지므로 스케일링 방식에 따라 결과가 크게 달라진다. 범주 수가 많은 변수는 차원축소 결과에서 과도한 영향력을 갖게 된다. ”범주 간 관계”가 아니라 ”더미 간 상관”을 요약하게 된다.

결국, 범주형 변수는 ’수치형처럼 보이게 만든 뒤 PCA’가 아니라,
범주형의 구조 자체를 반영하는 차원축소가 필요하다. 이 문제의식에서 출발한 방법이 MCA이며, 연속형과 범주형을 함께 다루기 위해 확장된 방법이 FAMD이다.

(2) 범주형 변수 차원축소: MCA (Multiple Correspondence Analysis)

MCA 개념

MCA는 범주형 변수만을 대상으로 한 차원축소 방법이다. 연속형 변수에서 PCA가 분산 구조를 요약하듯, MCA는 범주형 변수의 범주들 사이에 존재하는 관계 구조를 요약하는 것을 목표로 한다.

이를 위해 MCA는 각 범주형 변수를 더미(지시변수) 행렬로 변환하되,
단순히 이 행렬에 PCA를 적용하지 않고, 범주 출현 빈도를 반영한 χ²(카이제곱) 거리를 사용한다.
이 거리 개념은 범주가 우연히 많이 등장했는지, 아니면 특정 관측치들과 체계적으로 함께 나타나는지를 구분하도록 설계되어 있다. 그 결과 MCA는 개별 범주들의 단순한 상관관계를 요약하는 것이 아니라,
관측치–범주 행렬에서 나타나는 범주 간 ’동시 출현 패턴’을 가장 잘 설명하는 저차원 축을 도출한다.

즉, MCA는 범주형 변수들로 이루어진 데이터에서 범주 조합의 구조를 잠재 요인 공간으로 표현하는 차원축소 방법이다.

MCA 해석

MCA의 결과는 PCA와 유사하게 ”저차원 축과 좌표”로 제시되지만, 해석의 초점은 분산이 아니라 범주 조합이 어떻게 구분되는가에 있다. 먼저 MCA의 **축(axis)**은 여러 범주형 변수에서 나타나는 범주들의 결합 패턴을 요약한 것으로, 서로 다른 범주 조합을 가르는 잠재 요인으로 이해할 수 있다. 또한 **범주 좌표(category coordinates)**는 각 범주가 저차원 공간에서 어디에 위치하는지를 나타내며, 같은 축에서 서로 멀리 떨어진 범주일수록 관측치의 성향이 뚜렷하게 다르다는 뜻이다. 반대로 같은 방향에 놓인 범주들은 동일한 관측치에서 함께 관찰되는 경향이 커서, 동시 출현(co-occurrence) 관계가 강한 범주로 해석할 수 있다. 한편 **관측치 좌표(individual coordinates)**는 각 관측치가 어떤 범주 조합을 갖는지를 종합한 위치로, 특정 범주 조합을 대표하는 점으로 볼 수 있다. 따라서 MCA는 계수 추정이나 예측 정확도를 직접 높이기보다는, 범주형 데이터의 구조를 요약하고 시각화하여 패턴을 탐색하거나 군집 구조를 파악하는 데 특히 유용하다.

MCA 한계

다만 MCA에는 분명한 한계가 있다. 첫째, 방법론 자체가 범주형 변수의 관계 구조를 대상으로 하므로 연속형 변수를 직접 포함할 수 없다. 둘째, 범주 수준(level)이 많아질수록 좌표 해석이 급격히 복잡해지고, 중요한 범주를 선별하지 않으면 결과가 산만해지기 쉽다. 셋째, MCA는 반응변수 (Y)를 고려하지 않는 비지도 차원축소이므로, 결과가 반드시 예측 성능 향상으로 이어진다고 보장할 수 없으며 지도학습 목적에는 직접적이지 않다. 이러한 한계를 보완하기 위해 연속형과 범주형 변수를 동시에 다루는 혼합형 차원축소 방법이 제안되었고, 그 대표가 FAMD이다.

(3) 혼합형 차원축소: FAMD (Factor Analysis of Mixed Data)

FAMD 개념

FAMD(Factor Analysis of Mixed Data)는 연속형(측정형) 변수와 범주형 변수가 함께 존재하는 데이터를 위해 설계된 차원축소 방법이다. 혼합형 데이터에서는 연속형 변수는 자연스럽게 분산과 거리 개념을 갖지만, 범주형 변수는 라벨에 불과하므로 분산 기반의 PCA를 그대로 적용하기 어렵다. 범주형 변수를 더미로 변환해 PCA를 적용하는 방식도 가능하나, 범주 빈도와 스케일링 방식에 따라 결과가 왜곡될 수 있고, 범주 수준이 많은 변수가 과도한 영향력을 갖는 문제가 생긴다. 이러한 한계를 피하면서 혼합형 데이터의 구조를 안정적으로 요약하기 위해 FAMD가 사용된다.

FAMD 방법

FAMD의 핵심은 연속형 변수는 PCA처럼, 범주형 변수는 MCA처럼 다루되, 두 변수군이 차원축소 결과에 균형 있게 기여하도록 결합하는 데 있다. 먼저 연속형 변수는 평균 0, 분산 1이 되도록 표준화하여 변수 스케일 차이를 제거한 뒤, PCA와 동일한 방식으로 변동 구조가 반영되도록 한다. 반면 범주형 변수는 더미(지시) 변수로 변환하지만, 단순히 0/1 행렬로 취급하지 않고 각 범주의 출현 빈도를 고려하여 가중치를 부여한다. 구체적으로는 범주 빈도의 역수에 기반한 가중을 통해 드문 범주와 흔한 범주가 적절히 균형을 이루도록 조정하며, MCA에서 사용되는 χ² 거리 개념이 자연스럽게 반영되도록 만든다. 이렇게 연속형과 범주형을 각각 적절히 전처리한 뒤, 가중된 전체 행렬에 대해 단일 SVD(특이값 분해)를 수행함으로써 하나의 공통 좌표계에서 두 종류 변수 정보를 동시에 요약한다.

FAMD 특성

이 과정에서 FAMD는 중요한 성질을 갖는다. 즉, 연속형 변수 ”하나”와 범주형 변수 ”하나(여러 범주로 구성된 묶음)“가 차원축소 결과에 동일한 수준으로 기여하도록 설계되어, 범주형 변수를 억지로 연속형처럼 해석하거나 특정 범주형 변수가 과도하게 지배하는 현상을 완화한다. 또한 결과 해석의 틀은 PCA와 MCA의 관점을 그대로 유지한다. 고유값은 각 축이 전체 변동을 어느 정도 설명하는지를 나타내며, 이를 통해 몇 개의 축으로 차원을 줄일지 결정한다. 변수 기여도는 연속형 변수의 경우 PCA와 동일하게 해석되고, 범주형 변수의 경우에는 어떤 범주들이 특정 축을 형성하는지(어떤 대비가 축을 만드는지)를 확인함으로써 범주 구조를 이해할 수 있다. 관측치 좌표는 각 관측치가 연속형·범주형 특성을 동시에 반영한 위치로 표현된 것으로, 데이터의 군집 구조나 패턴을 시각적으로 탐색하는 데 유용하다.

따라서 FAMD는 주로 탐색적 데이터 분석(EDA) 단계에서 혼합형 데이터의 구조를 요약·시각화하거나, 회귀·군집·분류와 같은 분석을 수행하기 전에 차원을 줄이고 노이즈를 완화하는 전처리 단계로 활용된다. 특히 FAMD에서 얻은 축(점수)을 설명변수로 사용하면, 범주형 변수를 더미로 확장한 뒤 단순 PCA를 적용하는 방식보다 이론적으로 더 정당하고 해석이 안정적인 ”혼합형 PCR” 관점으로도 이해할 수 있다.

정리하면, 범주형 변수는 분산과 거리 개념이 자연스럽지 않기 때문에 PCA를 그대로 적용하기 어렵고, 범주형만을 대상으로 할 때는 MCA가 범주 간 관계 구조를 요약하는 역할을 한다. FAMD는 이 두 관점을 결합하여 연속형과 범주형이 함께 있는 상황에서 데이터 구조를 균형 있게 요약하는 혼합형 차원축소 방법이며, 예측 성능 최적화 자체보다는 구조 이해와 탐색, 시각화 목적에서 특히 유용하다.

(4) FAMD → 회귀(혼합형 PCR)

연속형 변수와 범주형 변수가 함께 존재하는 데이터에서 바로 선형회귀를 적용하면, 범주형 변수를 더미로 확장하면서 차원이 급격히 증가하고 다중공선성 문제가 심화되는 경우가 많다. 특히 설명변수의 수가 관측치 수에 비해 많아지거나, 범주 수준이 많은 변수가 포함되면 회귀계수의 불안정성과 해석의 어려움이 동시에 발생한다. 이러한 맥락에서 차원축소 후 회귀라는 접근은 자연스러운 해결책이 된다.

앞서 살펴본 FAMD는 혼합형 데이터의 구조를 비지도 방식으로 요약하는 차원축소 방법이다. 연속형 변수는 PCA의 원리에 따라 분산 구조를 반영하고, 범주형 변수는 MCA의 원리에 따라 범주 간 관계 구조를 반영하되, 두 변수군이 분석 결과에 균형 있게 기여하도록 설계되어 있다. 따라서 FAMD의 결과로 얻어지는 각 축은 특정 개별 변수나 범주를 그대로 나타내기보다는, 연속형·범주형 정보를 동시에 종합한 잠재 요인(latent components)으로 해석된다.

혼합형 PCR은 이러한 FAMD 축을 설명변수로 사용하여 회귀모형을 구성하는 접근이다. 절차는 개념적으로 단순하다. 먼저 반응변수 (Y)를 제외한 설명변수 집합 (X)에 대해 FAMD를 수행하여 저차원 축 점수(score)를 계산한다. 그 다음, 선택된 일부 FAMD 축들만을 새로운 설명변수로 사용하여 선형회귀모형을 적합한다. 이때 회귀의 대상이 되는 것은 원래의 연속형 변수나 더미 변수들이 아니라, 혼합형 데이터 구조를 요약한 FAMD 축이다.

이 접근의 장점은 여러 측면에서 드러난다. 첫째, 차원축소를 통해 설명변수의 수가 크게 줄어들어 다중공선성 문제가 완화되고, 회귀계수의 추정이 안정된다. 둘째, 범주형 변수를 더미로 확장한 뒤 임의적으로 스케일링하여 PCA를 적용하는 방식과 달리, FAMD는 범주 빈도와 구조를 고려하므로 이론적으로 더 정당한 전처리를 제공한다. 셋째, 회귀에 사용되는 축의 개수는 교차검증이나 검증오차를 기준으로 선택할 수 있어, 과적합을 제어하는 체계적인 기준을 제시한다.

다만 혼합형 PCR의 해석은 고전적인 회귀계수 해석과는 성격이 다르다. 개별 회귀계수는 특정 원변수의 직접적인 효과를 의미하지 않으며, 대신 각 FAMD 축이 반응변수와 얼마나 강하게 연관되는지를 해석의 중심에 두어야 한다. 따라서 ”어떤 변수가 얼마만큼 영향을 미치는가”보다는, ”어떤 연속형·범주형 구조가 반응변수와 관련되는가”를 이해하는 관점이 중요해진다.

6. 사례분석

(1) 데이터 개요

연비 mpg(연속형)를 예측하는 회귀 문제로 mpg는 값이 클수록 연비가 좋다는 것을 의미한다.

크기와 구조: 392개 관측치 × 9개 변수, 이는 df = df.dropna()로 결측이 있는 행을 제거한 결과

• 반응변수(Y): mpg
• 설명변수(X): cylinders, displacement, horsepower, weight, acceleration, model_year, origin, (name)
• 더미설명변수: cyl_group: cyl_34-203, cyl_8 -103, cyl_56-86 | origin: usa-245, japan-79, europe-68

import numpy as np
import pandas as pd
import seaborn as sns

# =========================
# 0) 데이터 불러오기 (가장 간단)
# =========================
df = sns.load_dataset("mpg")   # Auto MPG (Seaborn 내장 데이터)
# 필요시 결측 제거(특히 horsepower에 결측이 있는 경우가 흔함)
df = df.dropna()

# =========================
# 1) cylinders -> 3개 그룹
# =========================
df["cyl_group"] = np.select(
    [
        df["cylinders"].isin([3, 4]),
        df["cylinders"].isin([5, 6]),
        df["cylinders"].eq(8),
    ],
    ["cyl_34", "cyl_56", "cyl_8"],
    default="other"   # 문자열로 통일(에러 방지)
)

# 혹시 other가 있으면 확인(필요 시 제거)
if (df["cyl_group"] == "other").any():
    print("⚠️ 그룹에 안 들어간 cylinders 값:", sorted(df.loc[df["cyl_group"]=="other","cylinders"].unique()))
    # 필요하면 다음 줄로 제거
    # df = df.loc[df["cyl_group"] != "other"].copy()

# =========================
# 2) origin 값 정리(혹시 1/2/3 코드인 경우 대비)
# =========================
origin_map = {1: "usa", 2: "europe", 3: "japan"}
tmp = pd.to_numeric(df["origin"], errors="coerce")
if tmp.notna().all():  # 전부 숫자로 변환되면(=1/2/3 코딩)
    df["origin"] = tmp.astype(int).map(origin_map).astype("object")

# =========================
# 3) 더미변수(0/1) 생성 후 df에 붙이기
# =========================
cyl_dum = pd.get_dummies(df["cyl_group"], dtype=int).drop(columns=["other"], errors="ignore")
origin_dum = pd.get_dummies(df["origin"], prefix="origin", dtype=int)

df = pd.concat([df, cyl_dum, origin_dum], axis=1)

# 확인
print(df.info())

(2) 주성분 회귀(측정형 분석)

import numpy as np
import pandas as pd

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold, cross_val_score

# =========================
# 0) 반응변수/설명변수 (측정형만)
# =========================
y = df["mpg"].to_numpy()

X = df[["displacement", "horsepower", "weight", "acceleration", "model_year"]].copy()
X["weight"] = X["weight"].astype(float)
X["model_year"] = X["model_year"].astype(float)

# =========================
# 1) k 선택: 전체 데이터에서 K-fold CV
# =========================
max_k = X.shape[1]  # 5
cv = KFold(n_splits=10, shuffle=True, random_state=42)

cv_mse = []
for k in range(1, max_k + 1):
    pcr = Pipeline([
        ("scaler", StandardScaler()),
        ("pca", PCA(n_components=k, random_state=42)),
        ("lr", LinearRegression())
    ])
    scores = cross_val_score(pcr, X, y, cv=cv, scoring="neg_mean_squared_error")
    cv_mse.append(-scores.mean())

best_k = int(np.argmin(cv_mse) + 1)

print("CV MSE by #PCs:", {k: round(m, 4) for k, m in enumerate(cv_mse, start=1)})
print("Best #PCs (min CV MSE):", best_k)

# =========================
# 2) 최적 k로 전체 데이터에 최종 적합
# =========================
pcr_best = Pipeline([
    ("scaler", StandardScaler()),
    ("pca", PCA(n_components=best_k, random_state=42)),
    ("lr", LinearRegression())
])

pcr_best.fit(X, y)

# =========================
# 3) (선택) 결과 확인: 적재량/설명분산/회귀계수
# =========================
pca = pcr_best.named_steps["pca"]
lr = pcr_best.named_steps["lr"]

loadings = pd.DataFrame(
    pca.components_.T,
    index=X.columns,
    columns=[f"PC{i+1}" for i in range(pca.n_components_)]
)

print("\nExplained variance ratio:", pca.explained_variance_ratio_)
print("\nLoadings (variables -> PCs):")
display(loadings)

import statsmodels.api as sm
import pandas as pd

# =========================
# PCR(PC점수)로 OLS 적합 → p-value, R^2
# =========================

# 1) 표준화된 X 만들기 (pipeline의 scaler와 동일)
scaler = pcr_best.named_steps["scaler"]
pca = pcr_best.named_steps["pca"]

Z = scaler.transform(X)                 # (n, p)
T = pca.transform(Z)                    # (n, best_k) : PC scores

# 2) OLS 적합
X_ols = sm.add_constant(T)              # 절편 포함
ols = sm.OLS(y, X_ols).fit()

# 3) 회귀계수/유의확률 표
coef_table = pd.DataFrame({
    "coef": ols.params,
    "std_err": ols.bse,
    "t": ols.tvalues,
    "p_value": ols.pvalues
}, index=["Intercept"] + [f"PC{i+1}" for i in range(T.shape[1])])

print("=== PCR (on PC scores) OLS results ===")
print(f"R^2      : {ols.rsquared:.6f}")
print(f"Adj R^2  : {ols.rsquared_adj:.6f}\n")

display(coef_table)

# (선택) 전체 요약 출력
# print(ols.summary())

본 분석에서는 displacement, horsepower, weight, acceleration, model_year의 다섯 개 측정형 변수를 이용하여 주성분 회귀(PCR)를 수행하였다. 전체 데이터를 사용하여 10-fold 교차검증으로 주성분 개수를 선택한 결과, 다섯 개 주성분을 모두 사용하는 모형이 평균 제곱오차(CV MSE)를 최소화하였다. 이는 다섯 개 변수가 서로 강한 상관 구조를 가지지만, 여전히 각 주성분이 연비(mpg)를 설명하는 데 의미 있는 정보를 포함하고 있음을 시사한다.

선택된 주성분들의 분산 설명력을 보면, 제1주성분이 전체 변동의 약 68.2%를 설명하며 지배적인 축을 형성하고, 제2주성분과 제3주성분이 각각 약 16.2%, 12.9%를 추가로 설명한다. 나머지 두 주성분은 개별적으로 설명하는 분산은 작지만, 회귀 단계에서는 여전히 연비와의 관계를 통해 유의미한 역할을 할 수 있다.

주성분 점수에 대해 회귀모형을 적합한 결과, 결정계수 \(R^{2}\)는 약 0.809, 수정 결정계수는 약 0.806으로 나타났다. 이는 다섯 개 주성분을 통해 연비 변동의 약 81%를 설명할 수 있음을 의미헌다.

CV MSE by #PCs: {1: np.float64(18.0741), 2: np.float64(17.2532), 3: np.float64(13.1876), 4: np.float64(13.2102), 5: np.float64(12.083)}
Best #PCs (min CV MSE): 5
Explained variance ratio: [0.68212765 0.16180611 0.12939115 0.01624851 0.01042658]

제1주성분은 displacement, horsepower, weight에 모두 양의 적재량을 가지며, acceleration과 model_year에는 음의 적재량을 갖는다. 이는 차량의 크기와 중량, 엔진 규모가 함께 증가하는 구조를 나타내는 축으로 해석할 수 있다. 이 주성분의 회귀계수는 음수이며 통계적으로 매우 유의하여, 차량이 크고 무거울수록 연비가 유의하게 감소함을 보여준다. 따라서 제1주성분은 연비를 설명하는 가장 핵심적인 구조적 요인으로, ’차량 크기·중량 요인’으로 명명할 수 있다.

제2주성분은 model_year에 매우 큰 양의 적재량을 가지며, 다른 변수들의 기여는 상대적으로 작다. 이는 사실상 차량 연식을 대표하는 축으로, 기술 발전과 규제 변화에 따른 연비 개선 효과를 반영한다고 볼 수 있다. 회귀계수는 양수이고 유의하므로, 연식이 최신일수록 연비가 증가하는 경향이 통계적으로 뚜렷하게 나타난다. 따라서 제2주성분은 ’연식·기술 발전 요인’으로 해석된다.

제3주성분은 acceleration에 매우 큰 양의 적재량을 가지며, weight와 displacement도 함께 기여한다. 이는 단순한 차량 크기보다는 가속 성능 중심의 구조를 반영하는 축이다. 이 주성분의 회귀계수는 음수이고 매우 유의하여, 가속 성능을 강조한 차량일수록 연비가 감소하는 경향이 있음을 보여준다. 따라서 제3주성분은 ’가속 성능 중심 요인’으로 해석할 수 있다.

제4주성분은 horsepower에 큰 양의 적재량을 가지는 반면 displacement에는 음의 적재량을 보이며, 출력 대비 차체·엔진 구조의 대비를 반영하는 축으로 해석될 수 있다. 그러나 이 주성분의 회귀계수는 통계적으로 유의하지 않아, 이러한 구조적 차이는 연비 설명에 직접적인 기여를 하지 않는 것으로 나타난다.

제5주성분은 weight에 큰 양의 적재량을 가지면서 displacement와 horsepower에는 음의 적재량을 가진다. 이는 상대적으로 무거운 차체를 가지지만 엔진 규모나 출력은 작은 구조, 또는 그 반대를 대비시키는 축으로 볼 수 있다. 이 주성분의 회귀계수는 음수이며 통계적으로 유의하여, 중량 대비 엔진 효율이 불리한 구조가 연비를 크게 저하시킴을 시사한다.

Loadings (variables -> PCs):

	PC1	PC2	PC3	PC4	PC5
displacement	0.513005	0.191434	0.217898	-0.524760	-0.614269
horsepower	0.523657	0.092784	-0.046567	0.810110	-0.242337
weight	0.488276	0.272773	0.390052	-0.108031	0.723443
acceleration	-0.383340	0.051118	0.870528	0.233642	-0.195010
model_year	-0.277932	0.936870	-0.200976	0.045702	-0.050477

=== PCR (on PC scores) OLS results ===
R^2 : 0.808767
Adj R^2 : 0.806289

	coef	std_err	t	p_value
Intercept	23.445918	0.173503	135.132643	0.000000E+00
PC1	-3.544042	0.093948	-37.723302	1.526454E-131
PC2	1.080700	0.192897	5.602486	4.023481E-08
PC3	-2.553875	0.215710	-11.839409	8.439740E-28
PC4	0.694102	0.608717	1.140271	2.548803E-01
PC5	-4.595164	0.759891	-6.047139	3.483241E-09

(3) PLS 부분 최소제곱방법

import numpy as np
import pandas as pd

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.cross_decomposition import PLSRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import mean_squared_error, r2_score

import statsmodels.api as sm

# =========================
# 0) 반응변수/설명변수 (측정형만)
# =========================
y = df["mpg"].to_numpy()

X = df[["displacement", "horsepower", "weight", "acceleration", "model_year"]].copy()
X["weight"] = X["weight"].astype(float)
X["model_year"] = X["model_year"].astype(float)

# =========================
# 1) 성분 수 선택: 전체 데이터 10-fold CV (MSE 최소)
# =========================
max_k = X.shape[1]  # 5
cv = KFold(n_splits=10, shuffle=True, random_state=42)

cv_mse = []
for k in range(1, max_k + 1):
    pls = Pipeline([
        ("scaler", StandardScaler()),
        ("pls", PLSRegression(n_components=k))
    ])
    scores = cross_val_score(pls, X, y, cv=cv, scoring="neg_mean_squared_error")
    cv_mse.append(-scores.mean())

best_k = int(np.argmin(cv_mse) + 1)

print("CV MSE by #PLS components:", {k: round(m, 4) for k, m in enumerate(cv_mse, start=1)})
print("Best #PLS components (min CV MSE):", best_k)

# =========================
# 2) 최적 성분 수로 전체 데이터 최종 적합
# =========================
pls_best = Pipeline([
    ("scaler", StandardScaler()),
    ("pls", PLSRegression(n_components=best_k))
])
pls_best.fit(X, y)

# =========================
# 3) 전체 데이터에서 예측/적합도 (훈련 R^2)
# =========================
y_hat = pls_best.predict(X).ravel()
r2 = r2_score(y, y_hat)
mse = mean_squared_error(y, y_hat)
rmse = np.sqrt(mse)

print(f"\nTrain R^2  : {r2:.6f}")
print(f"Train RMSE : {rmse:.6f}")

# =========================
# 4) (선택) 성분 점수로 OLS 적합 → 성분 회귀계수 p-value
#    ※ 성분 수를 CV로 선택했으므로 p-value는 참고용
# =========================
scaler = pls_best.named_steps["scaler"]
pls = pls_best.named_steps["pls"]

Z = scaler.transform(X)                  # standardized X
T = pls.transform(Z)                     # (n, best_k) PLS scores

X_ols = sm.add_constant(T)
ols = sm.OLS(y, X_ols).fit()

coef_table = pd.DataFrame({
    "coef": ols.params,
    "std_err": ols.bse,
    "t": ols.tvalues,
    "p_value": ols.pvalues
}, index=["Intercept"] + [f"PLS{i+1}" for i in range(T.shape[1])])

print("\n=== PLS (on component scores) OLS results ===")
print(f"R^2      : {ols.rsquared:.6f}")
print(f"Adj R^2  : {ols.rsquared_adj:.6f}\n")
display(coef_table)

# =========================
# 5) (선택) 원변수 계수(표준화된 X 기준/원스케일 기준) 출력
# =========================
# sklearn PLSRegression의 coef_는 '표준화된 X' 기준 계수(스케일러 적용 후)로 해석하는 게 안전
beta_stdX = pls.coef_.ravel()  # standardized-X space

coef_stdX = pd.Series(beta_stdX, index=X.columns, name="coef (std-X space)")
print("\nCoefficients on standardized-X space:")
display(coef_stdX)

본 분석에서는 displacement, horsepower, weight, acceleration, model_year의 다섯 개 측정형 변수를 이용하여 부분최소제곱 회귀(PLS)를 수행하였다. 성분의 개수는 전체 데이터를 대상으로 한 10-fold 교차검증을 통해 선택하였으며, 평균제곱오차(CV MSE)가 최소가 되는 성분 수는 5개로 나타났다. 이는 본 자료에서 설명변수의 차원 수가 크지 않고, 각 성분이 반응변수인 연비(mpg)와 일정 수준 이상의 공분산 구조를 공유하고 있음을 시사한다.

선택된 5개의 PLS 성분을 이용해 전체 데이터에 회귀모형을 적합한 결과, 결정계수 \(R^{2}\)는 약 0.809, 수정 결정계수는 약 0.806으로 나타났다. 이는 측정형 변수만을 사용한 선형 구조 기반 모형으로 연비 변동의 약 81%를 설명할 수 있음을 의미하며, 앞서 수행한 PCR과 거의 동일한 수준의 설명력을 보인다. 다만 PLS는 성분을 구성하는 단계에서부터 반응변수 정보를 활용한다는 점에서, 동일한 성분 수를 사용하더라도 예측 지향적인 관점에서는 PCR보다 이론적으로 유리한 접근이다.

PLS 성분 점수에 대해 OLS 회귀를 수행한 결과를 보면, 제1성분부터 제4성분까지는 모두 통계적으로 유의한 회귀계수를 가지며, 제5성분만이 유의하지 않은 것으로 나타났다. 이는 앞의 네 개 성분이 연비와 직접적으로 연관된 구조적 요인을 포착하고 있음을 의미한다.

제1 PLS 성분의 회귀계수는 음수이며 매우 강한 유의성을 보인다. 이는 이 성분이 커질수록 연비가 크게 감소함을 의미한다. 원변수 계수를 함께 보면, weight가 가장 큰 음의 계수를 가지며, displacement와 horsepower는 상대적으로 작은 양의 계수를, model_year와 acceleration은 양의 방향으로 기여한다. 종합하면 제1성분은 차량 중량을 중심으로 한 ”차량 규모·중량 요인”을 강하게 반영하며, 중량이 증가할수록 연비가 급격히 악화되는 구조를 포착한 성분으로 해석할 수 있다. 이는 연비를 설명하는 가장 지배적인 요인이다.

제2 PLS 성분 역시 음의 회귀계수를 가지며 통계적으로 매우 유의하다. 이 성분은 제1성분과는 다른 방향의 공분산 구조를 통해 연비 감소 요인을 설명하며, 상대적으로 엔진 특성이나 성능 관련 변수들의 결합 효과를 반영한 축으로 볼 수 있다. 즉, 단순한 중량 효과와는 구분되는 또 하나의 구조적 연비 저하 요인을 포착한다.

제3 PLS 성분은 회귀계수의 크기는 작지만 여전히 통계적으로 유의하며, 연비 감소와 관련된 추가적인 미세 구조를 설명한다. 이는 주된 요인들에 비해 영향력은 작지만, 연비 변동을 보완적으로 설명하는 역할을 한다.

반면 제4 PLS 성분은 양의 회귀계수를 가지며 통계적으로 유의하다. 이는 해당 성분이 증가할수록 연비가 오히려 개선되는 방향의 구조를 반영함을 의미한다. 원변수 계수에서 model_year가 큰 양의 값을 가지는 점을 고려하면, 이 성분은 차량 연식과 기술 발전, 효율 개선 효과를 중심으로 한 요인을 반영한다고 해석할 수 있다. 즉, 최신 연식 차량일수록 동일한 물리적 제약 하에서도 연비가 개선되는 경향이 이 성분을 통해 포착된다.

제5 PLS 성분은 회귀계수가 통계적으로 유의하지 않아, 연비 설명에 추가적인 기여를 하지 않는 것으로 나타났다. 이는 교차검증 과정에서는 미세한 예측 개선 효과가 있었을 수 있으나, 전체 데이터 기준에서는 구조적으로 중요한 성분이라고 보기 어렵다는 것을 의미한다.

종합하면, 본 PLS 분석 결과는 연비가 단일 변수의 효과가 아니라, 차량 중량과 규모를 중심으로 한 물리적 구조, 엔진 및 성능 특성의 결합, 그리고 연식에 따른 기술 발전 효과라는 여러 공분산 구조의 결합에 의해 결정됨을 보여준다. 특히 PLS는 성분을 구성하는 단계에서부터 반응변수와의 연관성을 최대화하므로, PCR과 달리 ”연비를 설명하는 데 유리한 방향의 축”을 직접적으로 도출한다는 점이 강조된다. 이 점에서 PLS는 예측 중심의 분석이나, 설명변수 간 상관성이 강한 상황에서 연비와 직접적으로 연관된 구조를 파악하는 데 적합한 방법으로 해석할 수 있다.

CV MSE by #PLS components: {1: np.float64(16.219), 2: np.float64(12.9979), 3: np.float64(12.7626), 4: np.float64(12.1186), 5: np.float64(12.083)}
Best #PLS components (min CV MSE): 5
Train R^2 : 0.808767
Train RMSE : 3.408793

=== PLS (on component scores) OLS results ===
R^2 : 0.808767
Adj R^2 : 0.806289

	coef	std_err	t	p_value
Intercept	23.445918	0.173503	135.132643	0.000000E+00
PLS1	-3.661322	0.094979	-38.548899	2.059455E-134
PLS2	-2.260468	0.211284	-10.698701	1.437857E-23
PLS3	-1.008478	0.336388	-2.997958	2.893820E-03
PLS4	2.086204	0.437058	4.773293	2.576390E-06
PLS5	-0.291395	0.616808	-0.472424	6.368909E-01

PLS 회귀에서 표준화된 설명변수 공간에서의 회귀계수는, 각 변수가 평균 0, 분산 1로 정규화된 상태에서 연비(mpg)에 미치는 상대적 영향력의 크기와 방향을 비교하는 데 적합하다. 즉, 계수의 절댓값이 클수록 다른 변수들과의 상관 구조를 고려한 뒤에도 연비에 미치는 영향이 크다고 해석할 수 있다.

먼저 weight의 표준화 회귀계수는 −5.83으로 절댓값이 가장 크다. 이는 다른 모든 변수를 동시에 고려한 상태에서도 차량 중량이 연비에 미치는 영향이 압도적으로 크며, 중량이 증가할수록 연비가 크게 감소함을 의미한다. 단위와 스케일 차이를 제거한 상태에서조차 이 정도의 크기를 보인다는 점은, 연비 결정에서 중량이 가장 핵심적인 요인임을 분명히 보여준다.

다음으로 model_year의 계수는 +2.77로 두 번째로 크다. 이는 차량 연식이 최신일수록 연비가 유의하게 증가하는 경향이 강함을 나타낸다. 중량과는 반대 방향의 효과로, 기술 발전, 연료 효율 규제, 엔진 및 차체 설계 개선과 같은 구조적 변화가 연비 개선에 중요한 역할을 하고 있음을 시사한다.

displacement의 계수는 +0.29로 상대적으로 작지만 양의 값을 가진다. 이는 중량과 다른 변수들을 통제한 이후에는, 배기량 자체의 효과가 제한적이며 연비 감소 요인으로 작용하지 않거나 오히려 미세한 양의 방향으로 작용할 수 있음을 의미한다. 이는 배기량의 효과가 상당 부분 중량이나 출력과 결합된 형태로 이미 흡수되었기 때문으로 해석할 수 있다.

acceleration의 계수는 +0.25로 역시 크지 않은 양의 값을 보인다. 가속 시간이 길다는 것은(즉, 가속이 느리다는 것은) 상대적으로 효율 위주의 차량 특성을 반영하므로, 연비 개선 방향의 효과로 해석할 수 있다. 다만 그 영향력은 중량이나 연식에 비해 훨씬 작다.

마지막으로 horsepower의 계수는 +0.04로 거의 0에 가까운 값을 가진다. 이는 출력이 연비에 미치는 직접적인 영향은, 중량과 배기량, 가속 특성을 동시에 고려하면 거의 남지 않음을 의미한다. 즉, 출력의 연비 효과는 대부분 다른 변수들과의 공분산 구조를 통해 간접적으로 작용하며, 독립적인 설명력은 매우 제한적이다.

종합하면, 표준화 회귀계수 해석을 통해 연비는 개별 성능 지표들의 단순한 합으로 결정되기보다는, 차량 중량이라는 물리적 제약과 연식에 따른 기술적 진보라는 구조적 요인에 의해 지배적으로 설명됨을 알 수 있다. PLS 회귀는 이러한 구조를 반영하여, 중량과 연식의 효과를 가장 강하게 부각시키고, 배기량·출력·가속 성능과 같은 변수들의 영향은 상대적으로 부차적인 요인으로 정리해 준다. 이는 다중공선성이 강한 측정형 변수 집합에서 PLS가 ”연비와 가장 직접적으로 연관된 방향의 조합”을 성공적으로 추출하고 있음을 보여주는 결과이다.

Coefficients on standardized-X space:

	coef (std-X space)
displacement	0.290715
horsepower	0.039216
weight	-5.831154
acceleration	0.248872
model_year	2.774417

(4) FAMD + 주성분 회귀

# =========================
# 0) 준비: 라이브러리 설치/불러오기
# =========================
!pip -q install prince

import numpy as np
import pandas as pd
import seaborn as sns

import prince  # FAMD

# =========================
# 1) 데이터 로드 및 전처리
# =========================
df = sns.load_dataset("mpg").dropna().copy()

# (1) origin 정리: 1/2/3 코딩일 수도 있으니 방어적으로 처리
origin_map = {1: "usa", 2: "europe", 3: "japan"}
tmp = pd.to_numeric(df["origin"], errors="coerce")
if tmp.notna().all():  # 전부 숫자로 변환되면 (=1/2/3 코딩)
    df["origin"] = tmp.astype(int).map(origin_map)

# (2) cylinders -> cyl_group (3개 그룹)
df["cyl_group"] = np.select(
    [
        df["cylinders"].isin([3, 4]),
        df["cylinders"].isin([5, 6]),
        df["cylinders"].eq(8),
    ],
    ["cyl_34", "cyl_56", "cyl_8"],
    default="other"
)

# other가 남아있으면 제거(보통 seaborn mpg에서는 없지만 안전장치)
df = df.loc[df["cyl_group"] != "other"].copy()

# (3) 타입 지정(중요): 범주형은 category로
df["origin"] = df["origin"].astype("category")
df["cyl_group"] = df["cyl_group"].astype("category")

# =========================
# 2) FAMD 입력 데이터 구성
#    - 5개 측정형 + 2개 범주형(원형 유지)
# =========================
num_cols = ["displacement", "horsepower", "weight", "acceleration", "model_year"]
cat_cols = ["origin", "cyl_group"]

X_mixed = df[num_cols + cat_cols].copy()

# 반응변수(예: mpg)도 같이 둠
y = df["mpg"].to_numpy()

print(X_mixed.dtypes)

# =========================
# 3) FAMD 적합
# =========================
famd = prince.FAMD(
    n_components=5,      # 우선 5개(필요하면 늘리거나 CV로 선택)
    n_iter=10,
    copy=True,
    check_input=True,
    engine="sklearn",
    random_state=42
)

famd = famd.fit(X_mixed)

# (1) 관측치 좌표(=FAMD 점수)
Z = famd.row_coordinates(X_mixed)   # DataFrame (n x n_components)

# (2) 설명력(고유값/관성 비율에 해당)
eig = famd.eigenvalues_
inertia = famd.percentage_of_variance_  # 각 축 설명 비율(%)

print("\nEigenvalues:", eig)
print("Explained (%):", inertia)

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import r2_score, mean_squared_error

# =========================
# 4) FAMD 점수로 회귀: 성분 수 CV 선택
# =========================
max_k = Z.shape[1]
cv = KFold(n_splits=10, shuffle=True, random_state=42)

cv_mse = []
for k in range(1, max_k + 1):
    Xk = Z.iloc[:, :k].to_numpy()
    scores = cross_val_score(
        LinearRegression(), Xk, y, cv=cv,
        scoring="neg_mean_squared_error"
    )
    cv_mse.append(-scores.mean())

best_k = int(np.argmin(cv_mse) + 1)
print("CV MSE by #FAMD comps:", {k: round(m, 4) for k, m in enumerate(cv_mse, start=1)})
print("Best #FAMD comps:", best_k)

import statsmodels.api as sm
import pandas as pd
import numpy as np

# -------------------------
# 0) Dim 컬럼 이름 정리
# -------------------------
Z_ols = Z.copy()
if all(isinstance(c, (int, np.integer)) for c in Z_ols.columns):
    Z_ols.columns = [f"Dim{i+1}" for i in range(Z_ols.shape[1])]

# 선택된 DIM 개수(best_k = 5)
X_dim = Z_ols.iloc[:, :best_k].to_numpy()

# -------------------------
# 5) OLS 적합 (절편 포함)
# -------------------------
X_ols = sm.add_constant(X_dim)
ols = sm.OLS(y, X_ols).fit()

# -------------------------
# 6) 회귀계수 / 유의확률 표
# -------------------------
coef_table = pd.DataFrame({
    "coef": ols.params,
    "std_err": ols.bse,
    "t_value": ols.tvalues,
    "p_value": ols.pvalues
}, index=["Intercept"] + [f"Dim{i+1}" for i in range(best_k)])

print("=== FAMD → Regression (OLS) Results ===")
print(f"R^2     : {ols.rsquared:.6f}")
print(f"Adj R^2 : {ols.rsquared_adj:.6f}\n")

display(coef_table.round(6))

# (선택) 전체 요약
# print(ols.summary())

본 분석에서는 5개의 측정형 변수(displacement, horsepower, weight, acceleration, model_year)와 2개의 범주형 변수(origin, cyl_group)를 함께 사용하여 FAMD를 적용하고, 그 결과로 얻어진 5개의 차원(Dim1–Dim5)을 설명변수로 하여 연비(mpg)에 대한 회귀모형을 적합하였다. 차원 수는 전체 데이터를 기준으로 한 10-fold 교차검증에서 평균제곱오차를 최소화하는 값으로 5개가 선택되었다.

회귀모형의 결정계수는 \(R^{2}\)= 0.7758, 수정 결정계수는 0.7729로 나타났다. 이는 혼합형 변수를 구조적으로 요약한 5개의 FAMD 차원이 연비 변동의 약 78%를 설명하고 있음을 의미한다. 측정형 변수만을 사용한 PCR이나 PLS에 비해서는 설명력이 다소 낮지만, 범주형 변수를 포함한 혼합형 구조를 고려한 결과라는 점에서 충분히 높은 수준의 설명력으로 평가할 수 있다.

각 차원의 회귀계수와 유의확률을 살펴보면, Dim1, Dim2, Dim3, Dim5는 모두 통계적으로 매우 유의한 계수를 가지는 반면, Dim4는 유의하지 않은 것으로 나타났다. 이는 모든 FAMD 차원이 연비 설명에 동일하게 기여하는 것은 아니며, 일부 차원만이 연비와 직접적으로 연관된 구조를 담고 있음을 보여준다.

displacement float64
horsepower float64
weight int64
acceleration float64
model_year int64
origin category
cyl_group category

Eigenvalues: [7.59707625 4.67880448 4.17064433 3.9968149 3.95593726]
Explained (%): [1.04787259 0.64535234 0.57526129 0.55128481 0.54564652]

CV MSE by #FAMD comps: {1: np.float64(17.9309), 2: np.float64(16.8775), 3: np.float64(15.6097), 4: np.float64(15.7328), 5: np.float64(14.1384)}

Best #FAMD comps: 5
=== FAMD → Regression (OLS) Results ===
R^2 : 0.775837
Adj R^2 : 0.772934

	coef	std_err	t_value	p_value
Intercept	23.445918	0.187848	124.813234	0.000000
Dim1	-2.377761	0.068153	-34.888710	0.000000
Dim2	-0.491210	0.086841	-5.656416	0.000000
Dim3	-0.569780	0.091969	-6.195346	0.000000
Dim4	-0.050223	0.093949	-0.534582	0.593247
Dim5	-0.654921	0.094431	-6.935470	0.000000

import numpy as np
import pandas as pd

# -------------------------
# 0) Dim 컬럼 이름 정리
# -------------------------
Z_dim = Z.copy()
if all(isinstance(c, (int, np.integer)) for c in Z_dim.columns):
    Z_dim.columns = [f"Dim{i+1}" for i in range(Z_dim.shape[1])]
elif not all(str(c).startswith("Dim") for c in Z_dim.columns):
    Z_dim.columns = [f"Dim{i+1}" for i in range(Z_dim.shape[1])]

dims = list(Z_dim.columns)[:5]  # 선택된 5개 DIM

# -------------------------
# 1) 연속형 변수 vs DIM 상관 (직접 계산)
# -------------------------
X_num = X_mixed[num_cols].astype(float)
X_num_std = (X_num - X_num.mean()) / X_num.std(ddof=0)

corr_num = pd.DataFrame(index=num_cols, columns=dims, dtype=float)
for d in dims:
    corr_num[d] = [np.corrcoef(X_num_std[col].to_numpy(), Z_dim[d].to_numpy())[0, 1] for col in num_cols]

# -------------------------
# 2) 범주형 모달리티(범주) vs DIM 상관 (더미 0/1 ↔ DIM 상관)
# -------------------------
X_cat = X_mixed[cat_cols].copy()
dum = pd.get_dummies(X_cat, drop_first=False)  # 기준범주 제거하지 않음(모든 범주 사용)

corr_mod = pd.DataFrame(index=dum.columns, columns=dims, dtype=float)
for d in dims:
    corr_mod[d] = [np.corrcoef(dum[c].to_numpy(), Z_dim[d].to_numpy())[0, 1] for c in dum.columns]

# -------------------------
# 3) (선택) Dim → y 회귀계수 (이미 lr이 있으면 그것 사용)
# -------------------------
beta_dim = None
if "lr" in globals():
    try:
        beta_dim = pd.Series(lr.coef_.ravel()[:len(dims)], index=dims, name="beta (Dim -> y)")
    except Exception:
        beta_dim = None

# -------------------------
# 4) DIM별 요약 출력 함수
# -------------------------
def top_bottom(series, k=3):
    s = series.dropna().sort_values()
    bottom = s.head(k)
    top = s.tail(k)
    return bottom, top

print("========================================")
print("FAMD DIM1~DIM5 해석 근거 출력")
print(" - 연속형: 표준화 X와 DIM 상관")
print(" - 범주형: 더미(모든 범주)와 DIM 상관")
print("========================================\n")

# -------------------------
# 5) 전체 상관표도 원하면 마지막에 출력
# -------------------------
print("\n\n=== 전체 연속형 상관표(corr_num) ===")
display(corr_num.round(4))

print("\n=== 전체 모달리티 상관표(corr_mod) ===")
display(corr_mod.round(4))

Dim1의 회귀계수는 −2.38로 절댓값이 가장 크고, p-value가 0에 가깝게 나타나 통계적으로 매우 유의하다. 이는 Dim1이 증가할수록 연비가 크게 감소함을 의미한다. 앞서 Dim1이 차량의 크기·중량·배기량·출력과 대형 실린더(cyl_8), 미국 생산(origin_usa) 성향을 강하게 반영하는 구조적 축으로 해석되었음을 고려하면, 대형·중량·고출력 차량 구조가 연비를 악화시키는 핵심 요인임을 명확히 보여주는 결과이다. Dim1은 본 분석에서 연비를 설명하는 가장 지배적인 구조적 요인이다.

Dim2의 회귀계수는 −0.49로, Dim1에 비해서는 크기가 작지만 통계적으로 유의하다. 이는 Dim2가 증가할수록 연비가 감소하는 경향이 있음을 의미한다. Dim2는 주로 5–6기통(cyl_56) 차량 구조를 중심으로 한 대비 축으로 해석되었으므로, 중간 실린더 구성의 차량 특성이 연비 측면에서는 불리하게 작용하는 구조적 요인을 담고 있다고 볼 수 있다.

Dim3의 회귀계수는 −0.57로 역시 통계적으로 유의하며, 연비 감소 방향의 효과를 가진다. Dim3은 생산지 측면에서 유럽과 일본 차량의 대비, 그리고 연식(model_year)과 결합된 구조를 반영하는 축으로 해석되었다. 이 결과는 특정 생산 지역 및 설계·연식 특성이 연비에 부정적인 방향으로 작용하는 구조가 존재함을 시사한다. 다만 이는 개별 국가 효과라기보다는, 연속형 변수들과 결합된 구조적 패턴의 결과로 해석하는 것이 적절하다.

반면 Dim4의 회귀계수는 −0.05로 매우 작고, p-value가 약 0.59로 나타나 통계적으로 유의하지 않다. 이는 Dim4가 데이터의 구조를 요약하는 차원으로서는 의미를 가질 수 있으나, 연비를 설명하는 데에는 추가적인 정보를 거의 제공하지 않는다는 것을 의미한다. 따라서 해석의 우선순위에서는 Dim4를 보조적 또는 비핵심 차원으로 취급하는 것이 타당하다.

Dim5의 회귀계수는 −0.65로 비교적 크고, 통계적으로 매우 유의하다. 이는 Dim5가 연비 감소와 관련된 추가적인 구조를 담고 있음을 의미한다. 다만 Dim5는 연속형·범주형 변수와의 상관이 전반적으로 크지 않은 미세 구조 축이므로, 연비에 영향을 미치는 보조적 요인으로 해석하는 것이 적절하다.

종합하면, 본 FAMD 기반 회귀분석은 연비가 단일 변수의 효과로 결정되는 것이 아니라, 차량 규모와 중량 중심의 물리적 구조(Dim1), 실린더 구성에 따른 구조적 차이(Dim2), 생산지 및 연식과 결합된 설계 특성(Dim3), 그리고 **보조적인 미세 구조(Dim5)**의 결합에 의해 설명됨을 보여준다. 반면 Dim4는 연비 설명과 직접적인 관련성이 없는 구조적 변동으로 나타났다. 이 결과는 FAMD에서 도출된 차원을 회귀에 사용할 때, 모든 차원을 동일하게 해석하기보다는 반응변수와의 유의성을 기준으로 핵심 차원과 보조 차원을 구분해야 함을 잘 보여주는 사례이다.

마지막으로, 이 회귀계수의 유의확률은 FAMD 차원을 교차검증을 통해 선택한 뒤 동일한 데이터에 대해 추론한 결과이므로, 엄밀한 의미의 사후선택 추론은 아니다. 따라서 p-value는 참고적 지표로 활용하고, 해석의 중심은 각 차원이 담고 있는 구조적 의미에 두는 것이 바람직하다.

========================================
FAMD DIM1~DIM5 해석 근거 출력
- 연속형: 표준화 X와 DIM 상관
- 범주형: 더미(모든 범주)와 DIM 상관
========================================

=== 전체 연속형 상관표(corr_num) ===

	Dim1	Dim2	Dim3	Dim4	Dim5
displacement	0.9532	0.0180	-0.0302	-0.0212	0.0454
horsepower	0.9042	-0.1930	-0.0154	-0.0922	0.0495
weight	0.8756	0.0694	0.0271	0.0242	0.0993
acceleration	-0.6226	0.2865	0.1005	0.1389	0.0085
model_year	-0.4856	0.1607	-0.4158	0.1131	-0.1079

=== 전체 모달리티 상관표(corr_mod) ===

	Dim1	Dim2	Dim3	Dim4	Dim5
origin_europe	-0.3819	-0.1019	0.7143	-0.0267	-0.0519
origin_japan	-0.5035	-0.2748	-0.4639	-0.1869	0.1205
origin_usa	0.7159	0.3074	-0.1743	0.1757	-0.0593
cyl_group_cyl_34	-0.8246	-0.3856	0.0509	0.0829	-0.0636
cyl_group_cyl_56	0.0882	0.8151	-0.0589	-0.1403	0.0530
cyl_group_cyl_8	0.8532	-0.3287	-0.0024	0.0378	0.0223