MLDL 예측모형 | 트리기반

트리기반 예측모형

1. 트리기반 예측 개념

트리 기반 방법은 설명변수 공간을 여러 개의 단순한 영역으로 분할하는 방식이다. 어떤 관측치의 예측값은 보통 그 관측치가 속한 영역에 포함된 훈련 관측치들의 반응값 평균(회귀) 또는 최빈값(분류)으로 정한다. 설명변수 공간을 나누는 분할 규칙들의 집합은 트리 형태로 요약될 수 있으므로, 이러한 접근을 의사결정나무 방법이라고 부른다.

트리 기반 방법은 단순하고 해석이 쉽다. 그러나 예측 정확도 측면에서는, 지도학습 방법(회귀모형)들과 비교할 때 경쟁력이 떨어지는 경우가 많다. 따라서 이 장에서는 배깅, 랜덤 포레스트, 부스팅, Bayesian additive regression trees도 함께 소개한다. 이들 방법은 여러 개의 트리를 만든 뒤 이를 결합하여 하나의 합의 예측을 얻는다는 공통점을 가진다. 많은 수의 트리를 결합하면 해석 가능성이 일부 감소하는 대가로 예측 정확도가 크게 향상되는 경우가 많다.

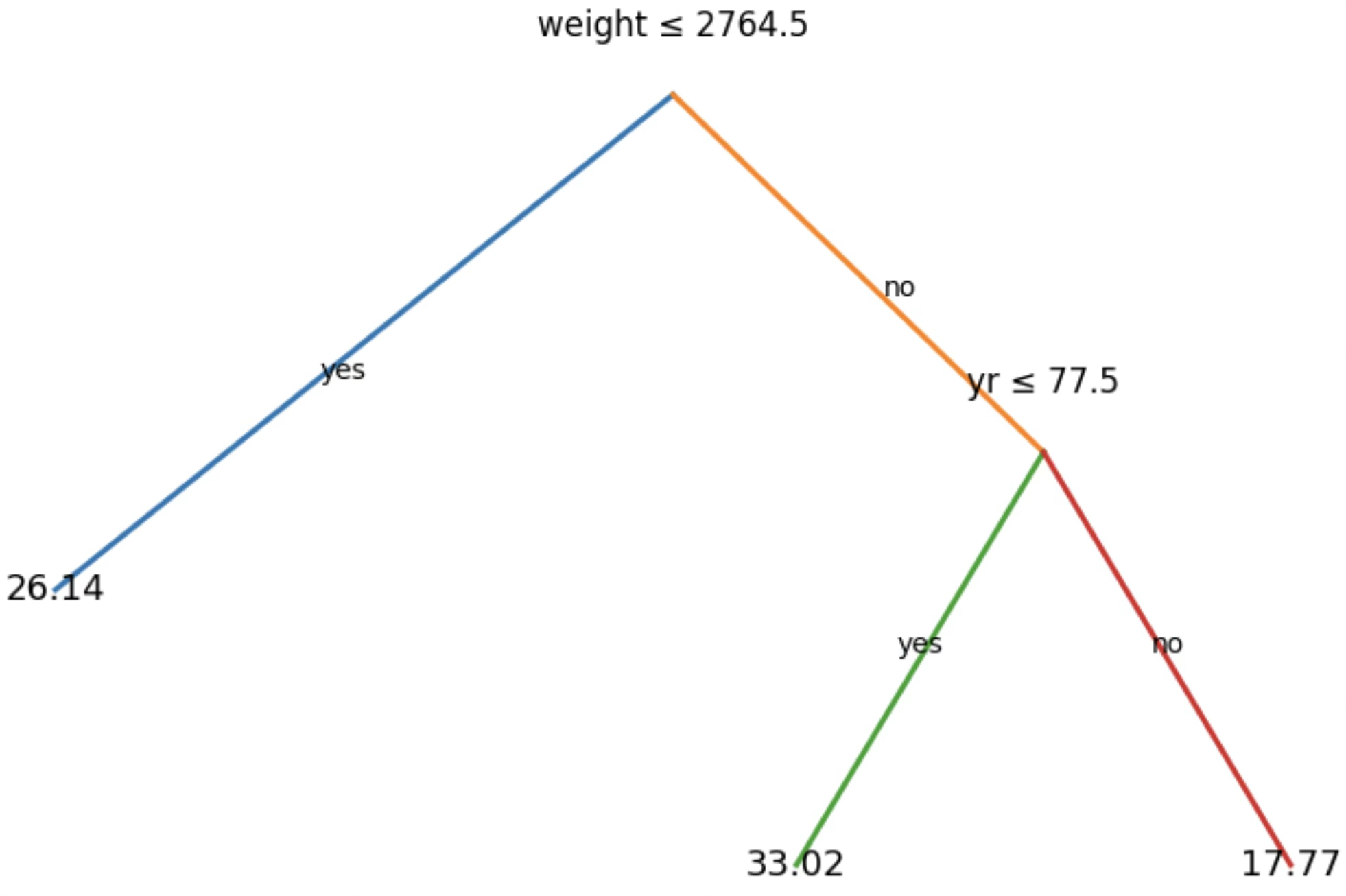
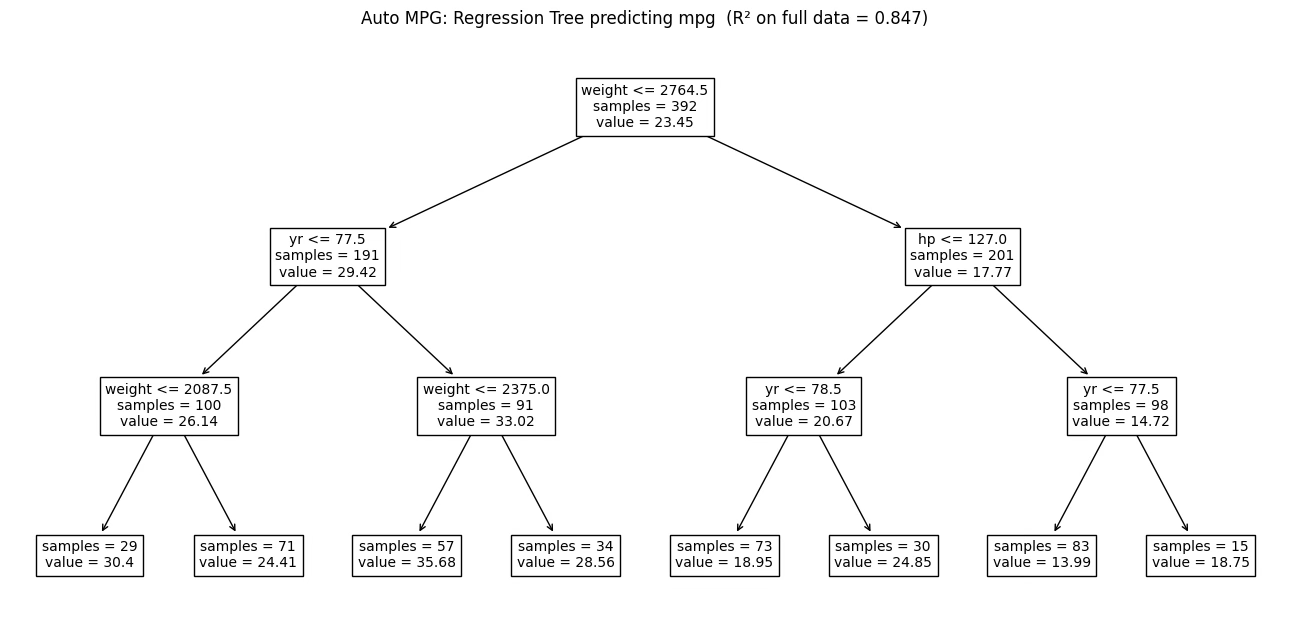
다음 그림은 MPG 데이터에 대해, 자동차의 연비(mpg)를 예측하기 위한 회귀나무이다. 사용된 설명변수는 차량 중량(weight)과 연식(yr, 70–82)이다. 각 내부 노드에서 ”Xj ≤ tk” 형태의 라벨은 해당 분할에서 왼쪽 가지로 내려가는 조건을 의미하며, 오른쪽 가지는 그 조건을 만족하지 않는 경우(즉 Xj > tk)에 해당한다. 예를 들어 맨 위 분할은 weight ≤ 2764.5 여부에 따라 두 개의 큰 가지로 나뉜다. 왼쪽 가지(weight가 가벼운 차량들)에서는 다시 yr ≤ 77.5로 한 번 더 분할되고, 오른쪽 가지(weight가 무거운 차량들)는 그대로 하나의 리프로 끝난다. 이 트리는 두 개의 내부 노드와 세 개의 리프를 가지며, 각 리프에 적힌 숫자는 그 리프에 속한 관측치들의 mpg 평균값을 의미한다.

2. 회귀나무(Regression Trees)

특징공간의 층화에 의한 예측

이제 회귀나무를 만드는 과정을 논의한다. 대략 두 단계가 있다.

1. 설명변수 공간, 즉 \(X_{1},X_{2},\ldots,X_{p}\)의 가능한 값들의 집합을, 서로 겹치지 않는 J개의 서로 다른 영역 \(R_{1},R_{2},\ldots,R_{J}\)로 나눈다.

2. 영역 \(R_{j}\)에 속하는 각 관측치에 대해 동일한 예측을 하는데, 이는 단순히 \(R_{j}\)에 속한 훈련 관측치들의 반응값 평균이다.

예를 들어 1단계에서 두 영역 \(R_{1}\)과 \(R_{2}\)를 얻었고, 첫 번째 영역에 속한 훈련 관측치들의 반응 평균이 10이며 두 번째 영역의 반응 평균이 20이라고 하자. 어떤 관측치 X = x에 대해, \(x \in R_{1}\)이면 10을 예측하고, \(x \in R_{2}\)이면 20을 예측한다.

회귀나무 정의

회귀나무는 설명변수 공간을 여러 개의 겹치지 않는 영역 \(R_{1},\ldots,R_{J}\)로 분할하고, 각 영역에 속하는 관측치에 대해서는 동일한 값(그 영역의 훈련 반응값 평균)으로 예측하는 방법이다. 즉, 관측치 x가 영역 \(R_{j}\)에 속하면 예측은 \(\widehat{f}(x) = {\widehat{y}}_{R_{j}}\)로 이루어지며, 여기서 \({\widehat{y}}_{R_{j}}\)는 \(R_{j}\)에 포함된 훈련 관측치들의 반응값 평균이다. 이때 ”좋은 분할”이란 전체 훈련 SSE를 작게 만드는 분할이며, 그 목적은 다음의 SSE를 최소화하는 영역 분할 \(R_{1},\ldots,R_{J}\)를 찾는 것이다.

\(\overset{J}{\sum_{j = 1}}\sum_{i:x_{i} \in R_{j}}(y_{i} - {\widehat{y}}_{R_{j}})^{2}\), 여기서 \({\widehat{y}}_{R_{j}}\)는 j번째 박스 안에 있는 훈련 관측치들의 반응 평균이다.

재귀적 이진 분할(recursive binary splitting)

그러나 설명변수 공간을 J개의 박스(고차원 직사각형)로 나누는 모든 경우를 전부 탐색하는 것은 계산적으로 불가능하므로, 회귀나무는 위에서 아래로 내려오며 한 번에 한 번씩 분할을 추가하는 재귀적 이진 분할(recursive binary splitting)을 사용한다. 이 절차는 탐욕적(greedy)인데, 각 단계에서 미래의 분할 가능성까지 고려한 전역 최적을 찾기보다, 그 단계에서 RSS를 가장 크게 줄이는 분할을 즉시 선택하기 때문이다.

재귀적 이진 분할에서 한 번의 분할은 어떤 변수 \(X_{j}\)와 컷포인트 s를 골라 설명변수 공간을 두 영역으로 나누는 것이다. 이때 두 영역은

\[R_{1}(j,s) = \{ X \mid X_{j} < s\},R_{2}(j,s) = \{ X \mid X_{j} \geq s\}\]

로 정의된다. 그리고 주어진 노드에서의 최적 분할은 가능한 모든 (j,s) 중에서, 분할 후 두 영역의 RSS 합이 최소가 되도록 하는 (j,s)를 선택하는 것으로 정해진다. 즉, \(\sum_{i:x_{i} \in R_{1}(j,s)}(y_{i} - {\widehat{y}}_{R_{1}})^{2} + \sum_{i:x_{i} \in R_{2}(j,s)}(y_{i} - {\widehat{y}}_{R_{2}})^{2}\)를 최소화하는 j와 s를 선택한다. 여기서 \({\widehat{y}}_{R_{1}}\)과 \({\widehat{y}}_{R_{2}}\)는 각각 \(R_{1}(j,s),R_{2}(j,s)\)에 속한 훈련 반응값의 평균이다. 이 과정을 반복하면 설명변수 공간은 점점 더 잘게 분할되고, 각 리프(종단 노드)에서의 예측은 그 리프에 속한 훈련 반응값 평균으로 고정된다.

알고리즘: 회귀나무 만들기(Building a Regression Tree)

1. 재귀적 이진 분할을 사용하여 훈련 데이터에서 큰 트리를 키운다. 각 종단 노드가 어떤 최소 관측치 수보다 적어질 때에만 멈춘다.

2. 큰 트리에 비용-복잡도 가지치기를 적용하여, \(\alpha\)의 함수로 ”최적 subtree”들의 수열을 구한다.

3. \(\alpha\)를 선택하기 위해 K-겹 교차검증을 사용한다. 즉, 훈련 관측치를 K개의 폴드로 나눈다. k = 1, …, K에 대해: (a) 훈련 데이터의 k번째 폴드를 제외한 나머지에 대해 1–2단계를 반복한다. (b) 제외해둔 k번째 폴드 데이터에서 평균제곱 예측오차를 α의 함수로 평가한다. 각 α 값에 대해 결과를 평균내고, 평균오차를 최소화하는 α를 선택한다.

4. 2단계에서 얻은 subtree들 중, 선택된 \(\alpha\) 값에 해당하는 subtree를 반환한다.

MPG 데이터 사례

목표: 종속변수 Y: mpg(연속형)
설명변수 X: 예를 들어 weight, yr(연식), horsepower 등

회귀나무가 하는 일: 설명변수 공간을 몇 개의 영역으로 나누고(분할), 각 영역에서는 mpg를 ”상수(평균)“로 예측한다.

예를 들어 weight와 yr만 써서 3개 리프(terminal node)를 갖는 작은 회귀나무는 다음 같은 형태가 된다.

1차 분할: weight ≤ 2764.5 ? yes → 예측 mpg = 26.14

no → 2차 분할: yr ≤ 77.5 ? yes → 예측 mpg = 33.02 | no → 예측 mpg = 17.77

해석은 ”무게가 가벼울수록 연비가 높고, 무거운 차들 중에서도 연식에 따라 연비 수준이 갈린다”처럼 규칙으로 읽으면 된다. 회귀나무에서 리프에 적힌 숫자는 그 리프에 속한 관측치들의 mpg 평균이다.

3. 분류나무(Classification Trees)

분류나무는 회귀나무와 매우 유사하지만, 정량적 반응이 아니라 정성적 반응을 예측하는 데 사용된다는 점이 다르다. 회귀나무에서는 어떤 관측치의 예측 반응값이, 같은 종단 노드(terminal node)에 속하는 훈련 관측치들의 반응값 평균으로 주어진다. 반면 분류나무에서는 각 관측치가 자신이 속한 영역에서 훈련 관측치들 중 가장 자주 나타나는 클래스에 속한다고 예측한다. 분류나무 결과를 해석할 때에는, 특정 종단 노드 영역에 대응하는 클래스 예측값뿐 아니라, 그 영역에 속한 훈련 관측치들에서의 클래스 비율(class proportions)에도 관심을 두는 경우가 많다.

분류 가지치기: 오분류율

분류나무를 성장시키는 과업은 회귀나무를 성장시키는 과업과 상당히 유사하다. 회귀 설정에서와 마찬가지로, 분류나무도 재귀적 이진 분할(recursive binary splitting)을 사용하여 성장시킨다. 그러나 분류 설정에서는 이진 분할을 만드는 기준으로 SSE를 사용할 수 없다. SSE에 대한 자연스러운 대안은 분류오류율(classification error rate)이다. 어떤 영역에 속한 관측치를 그 영역에서 가장 흔한 클래스에 할당할 계획이므로, 분류오류율은 그 영역 안의 훈련 관측치들 중 가장 흔한 클래스에 속하지 않는 관측치의 비율로 단순히 주어진다:

\(E = 1 - \max_{k}({\widehat{p}}_{mk})\), 여기서 \({\widehat{p}}_{mk}\)는 m번째 영역에서 k번째 클래스에 속하는 훈련 관측치의 비율을 나타낸다. 그러나 분류오류는 트리를 성장시키는 과정에서 충분히 민감하지 않은 것으로 밝혀져 다른 2가지 방법이 선호된다..

분류 가지치기: 지니 지수(Gini index)

\[G = \overset{K}{\sum_{k = 1}}{\widehat{p}}_{mk}(1 - {\widehat{p}}_{mk})\]

이는 K개 클래스에 걸친 전체 분산(total variance)의 한 측도이다. 모든 \({\widehat{p}}_{mk}\)가 0 또는 1에 가까우면 지니 지수는 작은 값을 갖는다는 것을 어렵지 않게 알 수 있다. 이러한 이유로 지니 지수는 노드 순도(node purity)의 측도로 불리는데, 값이 작다는 것은 그 노드가 주로 하나의 클래스 관측치들로 구성되어 있음을 의미한다.

분류 가지치기: 엔트로피(entropy)

\[D = - \overset{K}{\sum_{k = 1}}{\widehat{p}}_{mk}\log{\widehat{p}}_{mk}\]

\(0 \leq {\widehat{p}}_{mk} \leq 1\)이므로 \(0 \leq - {\widehat{p}}_{mk}\log{\widehat{p}}_{mk}\)가 성립한다. \({\widehat{p}}_{mk}\)들이 0 또는 1에 매우 가까우면 엔트로피는 0에 가까운 값을 갖는다는 것을 보일 수 있다. 따라서 지니 지수와 마찬가지로, m번째 노드가 순수할수록 엔트로피는 작은 값을 갖는다. 실제로 지니 지수와 엔트로피는 수치적으로 꽤 비슷한 결과를 주는 것으로 나타난다.

분류나무를 만들 때에는 특정 분할의 품질을 평가하기 위해 보통 지니 지수 또는 엔트로피를 사용한다. 이는 이 두 측도가 분류오류율보다 노드 순도에 더 민감하기 때문이다. 이 세 가지 접근 중 어느 것이든 트리를 가지치기(pruning)할 때 사용할 수 있지만, 최종적으로 가지치기된 트리의 예측 정확도가 목표라면 분류오류율이 선호된다.

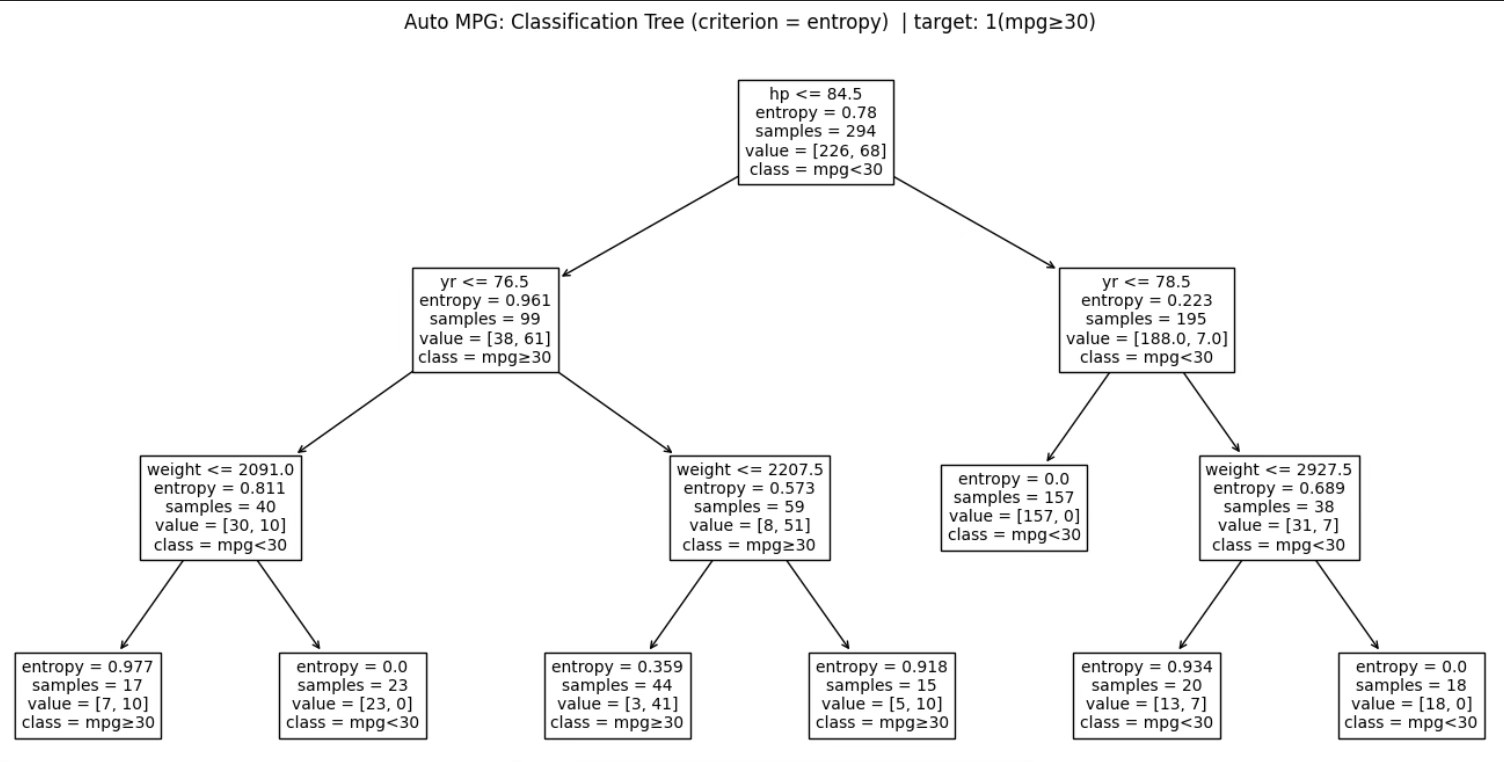
분류나무 예시: mpg를 ’고연비/저연비’로 바꿔

예측

회귀나무는 Y가 연속형일 때이고, 분류나무는 Y가 범주형일 때이다. Auto MPG는 원래 mpg가 연속형이므로, 분류나무 예시는 보통 mpg를 범주로 ”재코딩”해서 만든다.

목표(이진 분류) 종속변수 Y: 고연비 여부 예: Y=1 if mpg ≥ 30 (고연비) Y=0 if mpg < 30 (저연비)

설명변수 X: 예를 들어 weight 하나만 써도 가능, 혹은 weight, horsepower, yr 등

분류나무가 하는 일

각 영역(리프)에서 예측 클래스: 그 영역에서 가장 흔한 클래스(다수결) 또는 클래스 확률: 그 영역에서의 비율 \(\widehat{p}\)

weight만으로도 다음 같은 규칙이 나온다고 하자.

• weight ≤ 2200 → 예측: 고연비(1) (가벼운 차는 고연비가 많음)
• weight > 2200 → 예측: 저연비(0) (무거운 차는 저연비가 많음)

여기에 한 번 더 분할을 추가해서 weight > 2200인 영역을 다시 weight ≤ 2700 / > 2700으로 나누었는데 두 리프 모두 여전히 저연비(0)가 다수라서 예측 클래스는 둘 다 0일 수 있다.

그런데도 분할을 하는 이유는, 예측 클래스가 같더라도 ”순도(node purity)“가 달라지기 때문이다. 예컨대 매우 무거운 구간(>2700)에서는 거의 전부 저연비라 확신이 커지고(지니/엔트로피 감소), 2200~2700 구간은 고연비가 더 섞여 불확실성이 커진다. 그래서 분류오류율은 변하지 않아도 지니/엔트로피가 개선되는 분할이 생길 수 있다.

4. 가지치기와 복잡도 선택(Cost-Complexity Pruning)

필요성

의사결정나무는 설명변수 공간을 반복적으로 분할하여 훈련자료에 잘 맞는 예측 규칙을 만든다. 분할을 많이 허용하면 훈련오차는 계속 감소한다. 그러나 트리가 너무 깊어지면 자료의 우연한 변동(잡음)까지 따라가게 되어 분산이 커지고, 테스트 데이터에서의 예측 성능이 악화될 수 있다. 즉, 큰 트리는 과적합(overfitting)을 유발할 가능성이 높다. 또한 리프가 지나치게 많아지면 규칙이 과도하게 세분화되어 해석 가능성도 떨어진다. 따라서 트리의 복잡도를 적절히 줄여 일반화 성능과 해석 가능성을 확보하는 절차가 필요하며, 그 대표적 방법이 가지치기(tree pruning)이다.

개념

가지치기는 ”큰 트리”에서 불필요한 분할을 제거하여 더 단순한 서브트리(subtree)를 선택하는 과정이다. 이때 단순함은 보통 리프(terminal node) 수 |T| 또는 깊이로 표현된다. 가지치기의 핵심은 ”훈련 적합도”와 ”모형 복잡도” 사이의 절충을 명시적으로 다루는 데 있다. 이를 목적함수 관점에서 보면, 어떤 서브트리 T에 대해 \(\text{Loss}(T) + \alpha|T|\) 형태의 값을 최소화하는 트리를 선택하는 문제로 이해할 수 있다.

여기서 \(\text{Loss}(T)\)는 회귀나무에서는 SSE(또는 MSE 합)이고, 분류나무에서는 분류오류율 또는 불순도(지니/엔트로피)로 정의된다. \(\alpha \geq 0\)는 복잡도 패널티이며, \(\alpha\)가 커질수록 리프 수가 작은 단순한 트리가 선택되는 경향이 있다. 결국 가지치기는 ”조금 덜 맞추더라도(훈련오차 증가) 더 일반화가 잘 되도록(테스트오차 감소) 트리를 단순화하는 정규화(regularization)“로 해석된다.

가지치기는 회귀나무와 분류나무 모두에서 필수적인 일반화 성능 개선 절차이다. 큰 트리를 먼저 만든 뒤 복잡도를 줄여가는 방식이 근시안적 조기중단보다 안정적이며, 비용-복잡도 관점의 목적함수 \(\text{Loss}(T) + \alpha|T|\)로 통일해서 이해할 수 있다. 회귀는 \(\text{Loss}(T)\)가 SSE이며, 분류는 분류오류율 또는 불순도(지니/엔트로피)로 손실을 정의한다. 최종적으로는 교차검증을 통해 \(\alpha\) 또는 트리 크기를 선택하여, 과적합을 줄이고 해석 가능성과 예측력을 균형 있게 확보하는 것이 가지치기의 목적이다.

방법론

회귀나무에서는 리프마다 예측값이 해당 리프의 반응변수 평균이므로, 트리 적합도의 자연스러운 척도는 SSE이다. 큰 트리 \(T_{0}\)를 먼저 만든 뒤, 비용-복잡도 가지치기(cost-complexity pruning)를 통해 서브트리 \(T \subset T_{0}\)를 선택한다. 이때 최소화하려는 대표 목적함수는 \(\overset{|T|}{\sum_{m = 1}}\sum_{i:x_{i} \in R_{m}}(y_{i} - {\widehat{y}}_{R_{m}})^{2} + \alpha|T|\)이다. 첫 항은 트리의 훈련 SSE이며, 둘째 항은 리프 수에 대한 벌점이다. \(\alpha = 0\)이면 벌점이 없으므로 큰 트리가 유리하고, \(\alpha\)가 증가할수록 리프 수가 줄어든 단순한 트리가 선택된다.

실무에서는 여러 \(\alpha\) 값에 대해 만들어지는 서브트리들의 수열을 후보로 두고, 교차검증으로 예측오차가 최소가 되는 \(\alpha\)를 선택하여 최종 트리를 결정한다. 이 절차는 ”큰 트리 성장 → 서브트리 수열 생성 → 교차검증으로 \(\alpha\) 선택 → 선택된 \(\alpha\)의 서브트리 채택”의 순서로 정리된다.

분류나무에서 리프의 예측은 다수 클래스이며, 손실 척도로는 분류오류율(misclassification error), 지니 지수(Gini), 엔트로피(Entropy)가 대표적이다. 트리를 ”성장”시키는 단계에서는 분류오류율이 분할에 덜 민감한 경우가 많으므로, 노드 순도에 민감한 지니 또는 엔트로피를 사용해 분할을 선택하는 것이 일반적이다. 반면 최종 모델 선택, 즉 가지치기된 트리들 사이의 비교에서는 최종 목표가 예측 정확도인 경우가 많으므로 분류오류율(또는 정확도/오분류율)을 기준으로 교차검증을 수행하여 트리 크기를 선택하는 방식이 직관적이다.

결국 분류나무 가지치기는 ”복잡도 패널티 \(\alpha|T|\)“라는 구조는 같고, \(\text{Loss}(T)\) 자리에 분류오류율 또는 지니/엔트로피를 놓아 목적함수를 구성한다는 점만 다르다.

5. 트리기반 vs 선형모형

선형회귀는 다음 형태의 모형을 가정한다.

\[f(X) = \beta_{0} + \overset{p}{\sum_{j = 1}}X_{j}\beta_{j}\]

반면 회귀나무는 다음 형태의 모형을 가정한다.

\[f(X) = \overset{M}{\sum_{m = 1}}c_{m} \cdot \mathbf{1}(X \in R_{m})\]

어떤 모형이 더 나은가? 이는 당면한 문제에 달려 있다. 만약 특징들과 반응 사이의 관계가 선형모형으로 잘 근사된다면, 선형회귀 같은 접근이 대체로 잘 작동하며, 이러한 선형 구조를 활용하지 못하는 회귀나무 같은 방법보다 더 좋은 성능을 낼 가능성이 크다. 반대로, 특징들과 반응 사이에 매우 비선형적이고 복잡한 관계가 존재한다면, 의사결정나무가 고전적 접근법보다 더 좋은 성능을 낼 수 있다.

선형모형은 전역적으로 선형 구조(또는 지정한 비선형 변환)만 허용한다. 반면 트리는 국소적으로 규칙을 쌓아가는 방식이라 비선형성과 상호작용을 자연스럽게 흡수한다.

• 선형모형이 유리한 상황은 관계가 거의 선형이고, 해석(회귀계수)·추론(가설검정)이 중요한 상황이다.
• 트리가 유리한 상황은 상호작용이 강하고 비선형성이 크며, ”규칙 기반 설명”이 유용한 상황이다.

트리기반 장단점

트리 기반 방법은 회귀와 분류 문제 모두에 적용될 수 있으며, 고전적 방법(회귀)들에 비해 몇 가지 뚜렷한 장점을 가진다. 우선 의사결정나무는 구조가 규칙의 연쇄로 표현되기 때문에 사람에게 설명하기가 매우 쉽다. 경우에 따라서는 선형회귀보다도 설명이 더 간단한데, 이는 ”어떤 조건이면 왼쪽, 아니면 오른쪽”이라는 형태로 예측 규칙이 직관적으로 제시되기 때문이다.

또한 의사결정나무는 인간의 의사결정 과정을 단계적으로 모사하는 형태를 띠므로, 일부에서는 트리가 다른 회귀·분류 기법보다 인간의 판단 방식에 더 가깝다고 본다. 트리는 그림으로 나타낼 수 있고, 특히 트리가 작을 때는 비전문가도 전체 구조와 예측 규칙을 쉽게 해석할 수 있다는 점도 중요한 장점이다.

더불어 트리는 범주형(정성적) 예측변수를 다룰 때 더미변수로 변환하지 않고도 분할 규칙을 통해 직접 처리할 수 있어, 전처리 부담이 비교적 낮다.

반면 단일 트리는 예측 성능 측면에서 한계를 갖는 경우가 많다. 즉, 이 책에서 소개되는 다른 회귀·분류 방법들과 비교했을 때, 일반적으로 같은 수준의 예측 정확도를 보장하지 못하는 경우가 흔하다.

또한 트리는 비강건(non-robust)하다는 단점이 있다. 이는 데이터가 조금만 달라져도 분할 기준과 트리 구조가 크게 달라질 수 있음을 뜻하며, 결과적으로 예측 규칙이 불안정해질 수 있다는 의미이다.

이러한 단점에도 불구하고, 많은 의사결정나무를 결합하여 사용하는 앙상블 방법을 적용하면 트리의 예측 성능은 크게 향상될 수 있다. 배깅, 랜덤 포레스트, 부스팅은 여러 개의 트리를 만들어 결합함으로써 단일 트리의 불안정성과 예측력 한계를 보완하는 대표적 방법이며, 다음 절에서는 이러한 기법들을 본격적으로 다룬다.

6. 트리 앙상블 방법

(1) 앙상블 방법 필요 이유 및 개념

의사결정나무는 설명변수 공간을 여러 영역으로 분할하고, 각 영역에서 회귀는 평균값, 분류는 다수결(또는 클래스 확률)로 예측하는 규칙 기반 모형이다. 구조가 직관적이어서 해석과 시각화가 쉽고, 비선형성과 상호작용을 자동으로 반영한다는 장점이 있다. 그러나 단일 트리는 예측모형으로 사용할 때 구조적 한계를 가진다.

단일 트리의 가장 큰 약점은 예측이 불안정하다는 점이다. 트리는 재귀적 이진 분할이라는 탐욕적 절차로 만들어지는데, 데이터가 조금만 바뀌어도 분할 기준이 달라지고 결과 트리 구조가 크게 변할 수 있다. 이는 모형의 분산이 크다는 뜻이며, 테스트 데이터에서의 성능이 들쭉날쭉해질 수 있다. 또한 트리는 영역별로 상수 예측을 하기 때문에 예측함수가 계단형(piecewise constant)이고, 복잡한 관계를 충분히 잘 근사하려면 많은 분할이 필요하여 과적합 위험이 커진다. 반대로 과적합을 피하려고 트리를 너무 단순하게 제한하면 편향이 커져 예측력이 떨어질 수 있다. 즉 단일 트리는 편향–분산 관점에서 ”불안정(분산 큼)“하거나 ”너무 단순(편향 큼)”해지기 쉽다.

트리 앙상블은 하나의 트리 대신 여러 개의 트리를 학습시킨 뒤, 이들을 결합하여 하나의 최종 예측을 만드는 방법이다. 회귀 문제에서는 여러 트리의 예측을 평균내고, 분류 문제에서는 다수결(또는 확률 평균)로 결합한다. 앙상블의 핵심 아이디어는 ”개별 트리는 약하거나 불안정할 수 있지만, 여러 개를 적절히 모으면 더 정확하고 안정적인 예측기로 만들 수 있다”는 것이다.

회귀에서 트리 예측값을 평균내면, 개별 트리의 오차 중 우연한 변동 성분이 상쇄되면서 분산이 감소한다. 특히 트리처럼 분산이 큰 학습기는 평균을 통해 성능이 크게 안정화되는 경우가 많다. 다만 모든 트리가 비슷하면(서로 상관이 크면) 평균의 이점이 제한되므로, 앙상블은 ”트리들을 서로 다르게 만들고(다양성 확보), 그 결과를 결합”하는 방향으로 설계된다. 이 관점에서 배깅과 랜덤포레스트는 주로 분산을 줄이는 쪽에 초점을 맞추고, 부스팅은 순차적 보정으로 편향까지 줄이는 쪽으로 확장된다.

(2) 앙상블 방법 목적

앙상블 기법은 기본적으로 예측 정확도(일반화 성능)를 높이기 위해 사용된다. 하나의 모델만으로 예측을 수행하면, 학습 데이터의 우연한 특징이나 잡음에 의해 결과가 쉽게 흔들리거나(분산이 큼), 혹은 모델 자체가 너무 단순해서 복잡한 패턴을 충분히 담지 못하는 경우(편향이 큼)가 생긴다. 앙상블은 여러 개의 모델을 결합해 이런 약점을 완화함으로써, 새로운 데이터에서 더 안정적이고 정확한 예측을 얻고자 한다.

구체적으로 배깅과 랜덤포레스트는 동일한 종류의 모델을 여러 개 만들되, 데이터를 부트스트랩으로 조금씩 다르게 뽑아 각각 학습시키고 그 예측을 평균(회귀) 또는 투표(분류)로 합친다. 이렇게 하면 개별 모델이 가진 ”우연한 흔들림”이 서로 상쇄되어 전체 예측이 더 안정적으로 변하고, 결과적으로 테스트 데이터에서 성능이 좋아지는 경우가 많다. 특히 결정트리처럼 데이터 변화에 민감한 모델에서는 이 효과가 크게 나타난다. 랜덤포레스트는 여기서 더 나아가, 트리를 만들 때마다 일부 변수만 무작위로 후보에 올려 분할을 선택하게 함으로써 트리들 사이의 유사성을 줄이고, 평균 효과가 더 잘 작동하도록 만들어 분산을 추가로 낮춘다.

부스팅은 접근 방식이 다르다. 부스팅은 여러 모델을 순차적으로 학습시키면서, 앞 단계에서 잘 맞추지 못한 관측치나 패턴에 더 집중하도록 다음 모델을 보정해 나간다. 즉, 약한 학습기를 조금씩 쌓아가며 전체적으로 더 복잡하고 정교한 예측 함수를 만들어 편향을 줄이는 방향으로 성능을 끌어올린다. 다만 이 과정은 데이터의 잡음까지 과도하게 따라가면 과적합이 생길 수 있으므로, 학습률·트리 깊이·반복 횟수 같은 튜닝을 통해 복잡도를 적절히 통제하는 것이 중요하다.

결론적으로 앙상블은 단순히 ”훈련 데이터에서 점수를 올리기 위한 기술”이라기보다, 새 데이터에서도 잘 맞추도록(일반화 성능을 높이도록) 분산을 줄이거나 편향을 줄이는 방식으로 예측을 개선하는 방법이다. 다만 데이터가 매우 작거나 잡음이 큰 상황, 또는 이미 충분히 강하고 안정적인 단일 모델을 쓰는 상황에서는 성능 개선 폭이 크지 않을 수 있고, 모델의 해석 가능성은 대체로 떨어지는 경향이 있다.

(3) 배깅 Bagging

배깅 필요성

배깅은 단일 의사결정나무가 훈련 데이터의 작은 변화에도 분할 구조가 크게 달라지는 등 분산이 큰 모습을 보일 때 사용한다. 즉, 같은 문제를 두 개의 서로 다른 훈련 표본으로 학습했을 때 결과 트리와 예측 성능이 상당히 달라진다면, 예측을 안정화하기 위한 방법으로 배깅을 적용하는 것이 타당하다.

또한 단일 트리의 예측이 데이터에 따라 들쭉날쭉하여 안정적인 성능이 필요할 때 배깅이 유용하다. 비선형성과 상호작용이 강해 선형모형이 충분히 설명하지 못하는 상황에서도, 배깅은 복잡한 고성능 모델을 바로 적용하기 전에 강건한 기준선(baseline) 모델로 활용될 수 있다. 다만 배깅은 여러 개의 트리를 반복적으로 학습시키는 절차이므로, 표본 수가 어느 정도 충분하고 계산 자원이 허용되는 경우에 특히 적합하다.

배깅 사용방법

배깅은 적용 대상이 되는 문제 유형에 따라 결합 방식이 달라진다. 회귀 문제에서는 여러 개의 회귀나무가 산출한 예측값을 평균내어 연속형 반응변수 Y를 예측한다. 예를 들어 Auto MPG 데이터에서 mpg를 예측하거나, 주택 가격, 수요, 온도처럼 연속형 결과를 예측할 때 배깅 회귀나무를 사용할 수 있다. 반면 분류 문제에서는 각 트리가 예측한 클래스를 모아 다수결(또는 클래스 확률을 평균낸 뒤 최대 확률 클래스를 선택)로 최종 클래스를 결정한다. 따라서 질병 유무, 스팸 여부, 부도 여부처럼 범주형 반응을 예측하는 분류 문제에서도 배깅을 자연스럽게 적용할 수 있다.

배깅 정의

분산이 \(\sigma^{2}\)인 서로 독립인 n개의 관측치 \(Z_{1},\ldots,Z_{n}\)이 주어졌을 때, 그들의 평균 \(\overline{Z}\)의 분산은 \(\frac{\sigma^{2}}{n}\)으로 주어진다. 즉, 여러 관측치를 평균내면 분산이 감소한다. 따라서 통계적 학습 방법의 분산을 줄이고 테스트 정확도를 높이는 자연스러운 방법은, 모집단으로부터 많은 훈련셋을 얻어 각 훈련셋으로 별도의 예측모형을 만들고, 그 예측들을 평균내는 것이다.

B개의 서로 다른 훈련셋을 사용해 \({\widehat{f}}^{1}(x),{\widehat{f}}^{2}(x),\ldots,{\widehat{f}}^{B}(x)\)를 계산한 뒤 이를 평균내어, 다음과 같은 하나의 저분산 통계학습 모형을 얻을 수 있다.

\({\widehat{f}}_{\text{avg}}(x) = \frac{1}{B}\overset{B}{\sum_{b = 1}}{\widehat{f}}^{b}(x)\). 물론 이것은 일반적으로 여러 개의 훈련셋에 접근할 수 없기 때문에 실용적이지 않다. 대신 우리는 (하나의) 훈련 데이터셋으로부터 반복적으로 표본을 뽑는 방식으로 부트스트랩을 사용할 수 있다.

이 접근에서 우리는 서로 다른 B개의 부트스트랩 훈련 데이터셋을 생성한다. 그리고 b번째 부트스트랩 훈련셋에서 방법을 학습하여 \({\widehat{f}}^{*b}(x)\)를 얻고, 마지막으로 모든 예측을 평균내어 다음을 얻는다.

\({\widehat{f}}_{\text{bag}}(x) = \frac{1}{B}\overset{B}{\sum_{b = 1}}{\widehat{f}}^{*b}(x)\). 이를 배깅이라고 부른다.

배깅은 많은 회귀 방법에서 예측을 개선할 수 있지만, 특히 의사결정나무에 매우 유용하다. 회귀나무에 배깅을 적용하려면, B개의 부트스트랩 훈련셋을 사용해 B개의 회귀나무를 만들고, 그 예측을 평균내면 된다. 이 트리들은 깊게 성장시키며, 가지치기를 하지 않는다. 따라서 각 개별 트리는 분산이 크지만 편향은 낮다. B개의 트리를 평균내면 분산이 감소한다. 많은 수의 트리(수백 개 혹은 수천 개)를 하나의 절차로 결합함으로써 정확도가 크게 향상될 수 있음이 입증되어 왔다.

Out-of-Bag Error Estimation (OOB 오차 추정)

배깅 모형의 테스트 오차를, 교차검증이나 검증집합 접근을 수행하지 않고도 추정할 수 있는 매우 간단한 방법이 존재한다. 배깅의 핵심은 트리를 관측치들의 부트스트랩 부분집합에 반복적으로 적합한다는 점임을 상기하라. 평균적으로 배깅된 각 트리는 전체 관측치의 약 3분의 2 정도를 사용한다는 것을 보일 수 있다.

어떤 배깅된 트리를 적합하는 데 사용되지 않은 나머지 3분의 1 관측치들은 out-of-bag(OOB) 관측치라고 부른다. 우리는 i번째 관측치가 OOB였던 트리들 각각을 사용하여 i번째 관측치의 반응을 예측할 수 있다. 그러면 i번째 관측치에 대해 대략 B/3개의 예측을 얻게 된다. i번째 관측치에 대한 하나의 예측을 얻기 위해, (회귀가 목적이면) 이 예측 반응들을 평균내거나, (분류가 목적이면) 다수결을 취할 수 있다.

이렇게 하면 i번째 관측치에 대한 하나의 OOB 예측이 만들어진다. 이러한 방식으로 n개의 각 관측치에 대해 OOB 예측을 얻을 수 있고, 이를 통해 전체 OOB MSE(회귀 문제) 또는 분류오류(분류 문제)를 계산할 수 있다. 이렇게 얻은 OOB 오류는 배깅 모형의 테스트 오류에 대한 타당한 추정치인데, 각 관측치의 반응이 그 관측치를 사용하지 않고 적합된 트리들만으로 예측되기 때문이다.

Variable Importance Measures (변수 중요도 측정)

배깅은 단일 트리를 사용한 예측보다 정확도가 개선되는 결과를 보통 낳는다. 그러나 그 결과 모형을 해석하기가 어려울 수 있다. 의사결정나무의 장점 중 하나는 매력적이고 쉽게 해석되는 도식이 나온다는 점임을 상기하라.

하지만 많은 수의 트리를 배깅하면, 그 결과 통계적 학습 절차를 하나의 단일 트리로 표현하는 것이 더 이상 불가능해지고, 어떤 변수가 절차에서 가장 중요한지도 더 이상 명확하지 않다. 따라서 배깅은 해석 가능성을 희생하는 대가로 예측 정확도를 향상시킨다.

배깅된 트리들의 집합은 단일 트리보다 해석하기가 훨씬 어렵지만, RSS(배깅 회귀나무의 경우) 또는 지니 지수(배깅 분류나무의 경우)를 사용하여 각 예측변수의 중요도를 전체적으로 요약할 수 있다. 배깅 회귀나무에서는, 특정 예측변수로 분할함으로써 SSE가 감소한 총량을 기록할 수 있는데, 이를 B개의 모든 트리에 대해 평균낸다. 이 값이 크면 그 예측변수가 중요함을 의미한다. 유사하게 배깅 분류나무에서는, 특정 예측변수로 분할함으로써 지니 지수가 감소한 총량을 기록할 수 있고, 이를 B개의 모든 트리에 대해 평균낸다.

(4) 랜덤 포레스트 Random Forest

랜덤 포레스트는 트리들 사이의 상관을 낮추는(decorrelate) 작은 변경을 통해 배깅 트리보다 개선된 성능을 제공한다. 배깅과 마찬가지로, 우리는 부트스트랩된 훈련 표본들에서 여러 개의 의사결정나무를 만든다.

그러나 이러한 의사결정나무를 만들 때, 트리에서 어떤 분할을 고려할 때마다, 전체 p개의 예측변수 중에서 무작위로 선택된 m개의 예측변수를 분할 후보로 선택한다. 분할은 이 m개 예측변수 중 하나만을 사용할 수 있도록 제한된다. 각 분할마다 새로운 m개의 예측변수 표본을 다시 뽑으며, 일반적으로 \(m \approx \sqrt{p}\)를 선택한다. 즉, 각 분할에서 고려되는 예측변수의 개수는 전체 예측변수 개수의 제곱근과 대략 같도록 한다.

다시 말해, 랜덤 포레스트를 만들 때 트리의 각 분할에서 알고리즘은 사용 가능한 예측변수들의 ”대부분”을 고려하는 것조차 허용되지 않는다. 데이터셋에 매우 강력한 예측변수 하나가 있고, 그 밖에 중간 정도로 강한 예측변수들이 여러 개 있다고 가정하자. 그러면 배깅 트리들의 집합에서는 대부분 또는 거의 모든 트리가 맨 위 분할에서 이 강력한 예측변수를 사용할 것이다. 그 결과 배깅 트리들은 서로 매우 비슷해 보이게 된다. 따라서 배깅 트리들이 내놓는 예측은 서로 강하게 상관될 것이다.

불행히도 상관이 매우 큰 양들을 여러 개 평균낸다고 해서, 서로 독립(비상관)인 양들을 여러 개 평균내는 것만큼 분산이 크게 줄어들지는 않는다. 특히 이는 이러한 설정에서 배깅이 단일 트리에 비해 분산을 크게 줄이지 못한다는 의미가 된다.

랜덤 포레스트는 각 분할에서 예측변수들의 부분집합만을 고려하도록 강제함으로써 이 문제를 극복한다. 따라서 평균적으로 분할들의 \((p - m)/p\)비율은 그 강력한 예측변수를 아예 고려하지 못하게 되고, 그 결과 다른 예측변수들이 분할에 사용될 기회를 더 많이 갖게 된다. 우리는 이 과정을 트리들 사이의 상관을 낮추는(decorrelating) 과정으로 볼 수 있으며, 그 결과 트리들의 평균은 변동이 더 작고 따라서 더 신뢰할 수 있게 된다.

배깅과 랜덤 포레스트의 주된 차이는 예측변수 부분집합 크기 m의 선택이다. 예를 들어 랜덤 포레스트를 m=p로 만들어 버리면, 이는 단순히 배깅과 동일해진다.

(5) 부스팅 Boosting

이제 우리는 의사결정나무로부터 얻어지는 예측을 개선하기 위한 또 하나의 접근법인 부스팅(boosting)을 논의한다. 배깅과 마찬가지로, 부스팅은 회귀나 분류를 위한 많은 통계적 학습 방법에 적용될 수 있는 일반적인 접근법이다. 여기서는 부스팅에 대한 논의를 의사결정나무의 맥락으로 제한한다.

배깅은 부트스트랩을 사용하여 원래의 훈련 데이터셋의 여러 복사본을 만들고, 각 복사본에 별도의 의사결정나무를 적합한 다음, 모든 트리를 결합하여 하나의 예측모형을 만드는 절차임을 상기하라. 특히 각 트리는 다른 트리들과 무관하게, 부트스트랩된 데이터셋 위에서 구축된다. 부스팅도 비슷한 방식으로 작동하지만, 트리들이 순차적으로(sequentially) 성장한다는 점이 다르다. 즉, 각 트리는 이전에 성장한 트리들로부터 얻은 정보를 사용하여 성장한다. 부스팅은 부트스트랩 표본추출을 포함하지 않는다. 대신 각 트리는 원래 데이터셋을 수정한(modified) 버전 위에서 적합된다.

알고리즘 회귀나무를 위한 부스팅

1. \(\widehat{f}(x) = 0\)으로 두고, 훈련셋의 모든 i에 대해 \(r_{i} = y_{i}\)로 둔다.

2. \(b = 1,2,\ldots,B\)에 대해 다음을 반복한다. (a) 훈련 데이터 (X,r)에 대해 d번 분할(즉 d+1개의 종단 노드를 갖는) 트리 \({\widehat{f}}^{b}\)를 적합한다. (b) 새로운 트리의 축소된(shrunken) 버전을 더하여 \(\widehat{f}\)를 갱신한다: \(\widehat{f}(x) \leftarrow \widehat{f}(x) + \lambda{\widehat{f}}^{b}(x)\) (c) 잔차를 갱신한다. \(r_{i} \leftarrow r_{i} - \lambda{\widehat{f}}^{b}(x_{i})\)

3. 부스팅된 모형을 출력한다. \(\widehat{f}(x) = \overset{B}{\sum_{b = 1}}\lambda{\widehat{f}}^{b}(x)\)

트리의 개수 B이다. 배깅과 랜덤 포레스트와 달리, 부스팅은 B가 너무 크면 과적합이 발생할 수 있다. 다만 이런 과적합은 매우 천천히 발생하거나 아예 발생하지 않는 경향도 있다. 우리는 교차검증으로 B를 선택한다.

축소(shrinkage)** 파라미터 \(\lambda\)이다**. 이는 작은 양수이며, 부스팅이 학습하는 속도를 조절한다. 전형적인 값은 0.01 또는 0.001이며, 적절한 값은 문제에 따라 달라질 수 있다. \(\lambda\)가 매우 작으면 좋은 성능을 얻기 위해 매우 큰 B가 필요할 수 있다.

각 트리에서의 분할 수 d이다. 이는 부스팅 앙상블의 복잡도를 조절한다. 종종 d=1이 잘 작동하는데, 이 경우 각 트리는 하나의 분할만 가진 stump가 된다. 이 경우 부스팅 앙상블은 가법모형(additive model)을 적합하게 되는데, 각 항이 단 하나의 변수만을 포함하기 때문이다. 더 일반적으로 d는 상호작용 깊이(interaction depth)이며, 부스팅된 모형의 상호작용 차수를 조절한다. 즉 d번의 분할은 최대 d개의 변수가 관여할 수 있다.

이 절차의 아이디어는 무엇인가? 데이터에 하나의 큰 의사결정나무를 적합하는 것은 데이터를 매우 강하게 맞추는 것이며, 과적합으로 이어질 수 있다. 반면 부스팅 접근은 천천히 학습한다.

현재의 모형이 주어졌을 때, 우리는 그 모형의 잔차(residuals)에 대해 의사결정나무를 적합한다. 즉, 반응변수로 결과 Y를 쓰는 대신, 현재 잔차를 반응변수로 하여 트리를 적합한다.

그런 다음 이 새로운 의사결정나무를 적합된 함수에 더하여 잔차를 갱신한다. 알고리즘의 파라미터 d에 의해 결정되는 것처럼, 이러한 트리들 각각은 몇 개의 종단 노드만 갖는 꽤 작은 트리일 수 있다.

잔차에 대해 작은 트리를 적합함으로써, 모형이 잘 수행하지 못하는 영역에서 \(\widehat{f}\)를 서서히 개선한다. 축소 파라미터 \(\lambda\)는 이 과정을 더 느리게 하여, 더 많은 수의 그리고 형태가 서로 다른 트리들이 잔차를 ”공격”할 수 있게 한다. 일반적으로 천천히 학습하는 통계적 학습 방법은 좋은 성능을 내는 경향이 있다. 배깅과 달리, 부스팅에서는 각 트리의 구성은 이미 성장한 트리들에 강하게 의존한다는 점에 유의하라.

(6) 베이지안 가법 회귀나무(Bayesian Additive Regression Trees)

단순화를 위해, 여기서는 분류가 아니라 회귀를 위한 BART만을 제시한다. 배깅과 랜덤 포레스트는 회귀나무들의 평균으로부터 예측을 만들며, 각 트리는 데이터와/또는 예측변수의 무작위 표본을 사용하여 구축된다. 각 트리는 다른 트리들과 분리되어 독립적으로 만들어진다.

K는 회귀나무의 개수를, B는 BART 알고리즘을 실행할 반복(iteration) 횟수를 나타내도록 하자. \({\widehat{f}}_{k}^{b}(x)\)는 b번째 반복에서 사용되는 k번째 회귀나무의, x에서의 예측을 나타낸다. 각 반복의 끝에서, 해당 반복에서의 K개의 트리를 합해 \({\widehat{f}}^{b}(x) = \overset{K}{\sum_{k = 1}}{\widehat{f}}_{k}^{b}(x),b = 1,\ldots,B\)로 둔다.

BART 알고리즘의 첫 번째 반복에서, 모든 트리는 하나의 루트 노드만 갖도록 초기화되며, \({\widehat{f}}_{k}^{1}(x) = \frac{1}{nK}\overset{n}{\sum_{i = 1}}y_{i}\)로 둔다. 즉 반응값 평균을 트리 개수로 나눈 값이다. 따라서 \({\widehat{f}}^{1}(x) = \overset{K}{\sum_{k = 1}}{\widehat{f}}_{k}^{1}(x) = \frac{1}{n}\overset{n}{\sum_{i = 1}}y_{i}\)가 된다.

이후 반복들에서 BART는 K개의 트리를 하나씩 갱신한다. b번째 반복에서 k번째 트리를 갱신하기 위해, 각 반응값에서 k번째 트리를 제외한 나머지 모든 트리의 예측을 빼서 부분 잔차(partial residual)를 얻는다. \(r_{i} = y_{i} - \sum_{k' < k}{\widehat{f}}_{k'}^{b}(x_{i}) - \sum_{k' > k}{\widehat{f}}_{k'}^{b - 1}(x_{i}),i = 1,\ldots,n\)

이 부분 잔차에 대해 새로운 트리를 ”새로” 적합하는 대신, BART는 가능한 여러 섭동(perturbation)들 가운데 하나를 무작위로 선택하여 이전 반복에서의 트리 \({\widehat{f}}_{k}^{b - 1}\)를 변화시키며, 부분 잔차에 대한 적합을 개선하는 섭동이 선호되도록 한다. 이 섭동에는 두 가지 구성요소가 있다.

1. 가지(branch)를 추가하거나 가지치기(pruning)하여 트리의 구조를 바꿀 수 있다.

2. 트리의 각 종단 노드에서의 예측값을 바꿀 수 있다.

BART의 출력은 예측모형들의 모음(collection)이며, \({\widehat{f}}^{b}(x) = \overset{K}{\sum_{k = 1}}{\widehat{f}}_{k}^{b}(x),b = 1,2,\ldots,B\)로 주어진다.

일반적으로 초기의 몇 개 예측모형은 성능이 좋지 않은 경향이 있으므로 버린다. 이러한 초기 반복 구간을 burn-in 기간이라고 부른다. burn-in 반복 횟수를 L로 두자(예: L=200). 그러면 하나의 최종 예측을 얻기 위해, burn-in 이후 반복들의 평균을 취해 \(\widehat{f}(x) = \frac{1}{B - L}\overset{B}{\sum_{b = L + 1}}{\widehat{f}}^{b}(x)\)로 둔다. 그러나 평균 외의 다른 양도 계산할 수 있는데, 예컨대 \({\widehat{f}}^{L + 1}(x),\ldots,{\widehat{f}}^{B}(x)\)의 분위수는 최종 예측의 불확실성을 측정하는 데 사용될 수 있다.

알고리즘 베이지안 가법 회귀나무(Bayesian Additive Regression Trees)

1. \({\widehat{f}}_{1}^{1}(x) = {\widehat{f}}_{2}^{1}(x) = \cdots = {\widehat{f}}_{K}^{1}(x) = \frac{1}{nK}\overset{n}{\sum_{i = 1}}y_{i}\)로 둔다.

2. \({\widehat{f}}^{1}(x) = \overset{K}{\sum_{k = 1}}{\widehat{f}}_{k}^{1}(x) = \frac{1}{n}\overset{n}{\sum_{i = 1}}y_{i}\)를 계산한다.

3. \(b = 2,\ldots,B\)에 대해 (a) \(k = 1,\ldots,K\)에 대해 (1) \(i = 1,\ldots,n\)에 대해 현재의 부분 잔차를 계산한다: \(r_{i} = y_{i} - \sum_{k' < k}{\widehat{f}}_{k'}^{b}(x_{i}) - \sum_{k' > k}{\widehat{f}}_{k'}^{b - 1}(x_{i})\) (2) 새로운 트리 \({\widehat{f}}_{k}^{b}(x)\)를 \(r_{i}\)에 적합한다. 이때 이전 반복의 k번째 트리 \({\widehat{f}}_{k}^{b - 1}(x)\)를 무작위로 섭동하여 적합하며, 적합을 개선하는 섭동이 선호되도록 한다. (b) \({\widehat{f}}^{b}(x) = \overset{K}{\sum_{k = 1}}{\widehat{f}}_{k}^{b}(x)\)를 계산한다.

4. L개의 burn-in 샘플 이후 평균을 계산한다: \(\widehat{f}(x) = \frac{1}{B - L}\overset{B}{\sum_{b = L + 1}}{\widehat{f}}^{b}(x)\)

(7) 트리 앙상블 방법 요약

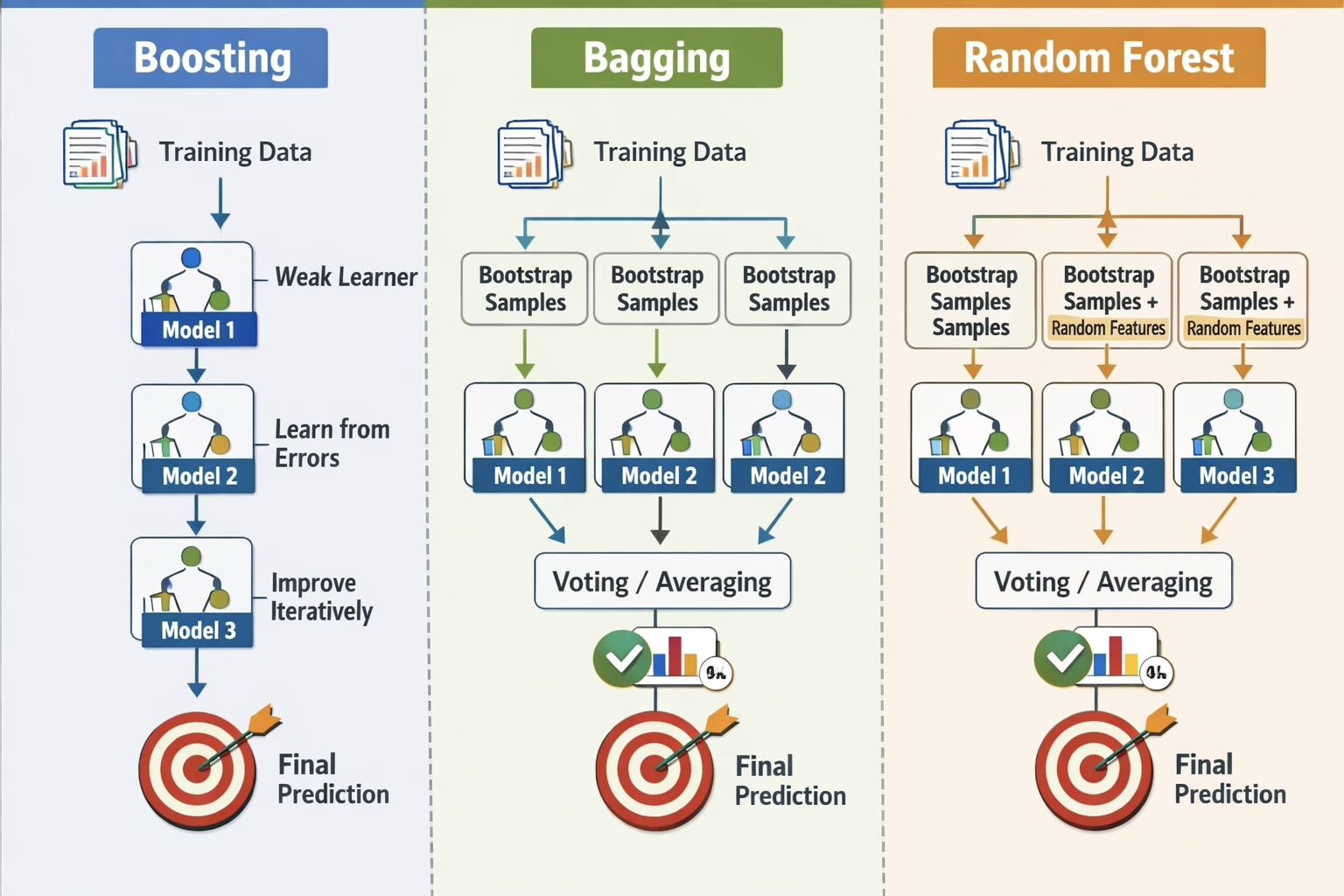
배깅에서는 트리들이 관측치의 무작위 표본들에서 서로 독립적으로 성장한다. 그 결과 트리들은 서로 꽤 비슷해지는 경향이 있다. 따라서 배깅은 국소 최적(local optima)에 갇힐 수 있고, 모형 공간(model space)을 충분히 탐색하지 못할 수도 있다.

랜덤 포레스트에서는 트리들이 다시 관측치의 무작위 표본들에서 서로 독립적으로 성장한다. 그러나 각 트리의 각 분할은 특징들의 무작위 부분집합을 사용하여 수행되며, 이로써 트리들 간 상관을 낮추고(decorrelate) 배깅에 비해 모형 공간을 더 철저하게 탐색하게 된다.

부스팅에서는 원래 데이터만을 사용하며 어떤 무작위 표본도 추출하지 않는다. 트리들은 ”느린(slow)” 학습 접근을 사용하여 순차적으로 성장한다. 즉, 각 새로운 트리는 이전 트리들에서 남아 있는 신호(signal)에 맞추어 적합되며, 사용되기 전에 축소(shrinkage)된다.

BART에서는 역시 원래 데이터만을 사용하며 트리들을 순차적으로 성장시킨다. 그러나 각 트리는 국소 최적을 피하고 모형 공간을 더 철저하게 탐색하기 위해 섭동(perturbation)된다.

7. 사례분석

(1) 데이터

회귀나무

Y(예측 대상): mpg
X(설명변수): displacement, horsepower, weight, acceleration, model_year, origin (실린더는 삭제하였음)
origin: 범주형이므로 원-핫 인코딩 후 사용한다.

분류나무
Y(예측 대상): \(mpg \geq 25\)-고연비, \(mpg < 25\)-저연비

(2) 회귀나무

최적 모수 출력

import numpy as np
import pandas as pd
import seaborn as sns

from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt

# 0) 데이터
df = sns.load_dataset("mpg").dropna()

# 1) Y, X 정의
y = df["mpg"]
X = df[["displacement", "horsepower", "weight",
        "acceleration", "model_year", "origin"]]

num_cols = ["displacement", "horsepower", "weight", "acceleration", "model_year"]
cat_cols = ["origin"]

# 2) 전처리: origin만 원-핫, 수치형은 그대로
preprocess = ColumnTransformer(
    transformers=[
        ("cat", OneHotEncoder(handle_unknown="ignore"), cat_cols),
        ("num", "passthrough", num_cols),
    ]
)

# 3) train/test split
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 4) 회귀나무 + 튜닝
pipe = Pipeline([
    ("prep", preprocess),
    ("tree", DecisionTreeRegressor(random_state=42))
])

param_grid = {
    "tree__max_depth": [2, 3, 4, 5, 8, None],
    "tree__min_samples_leaf": [1, 3, 5, 10, 20],
    "tree__ccp_alpha": [0.0, 0.001, 0.005, 0.01, 0.02]
}

gs = GridSearchCV(
    pipe, param_grid=param_grid,
    cv=5, scoring="neg_root_mean_squared_error",
    n_jobs=-1
)
gs.fit(X_train, y_train)

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

pred_test = best_reg.predict(X_test)

mse  = mean_squared_error(y_test, pred_test)
rmse = np.sqrt(mse)
mae  = mean_absolute_error(y_test, pred_test)
r2   = r2_score(y_test, pred_test)

print(
    "Best params:", gs.best_params_,
    "| Test RMSE:", rmse,
    "| Test MAE:", mae,
    "| Test R^2:", r2
)

GridSearchCV로 회귀나무(DecisionTreeRegressor)의 하이퍼파라미터를 탐색한 결과, 교차검증 기준(neg RMSE)에서 가장 성능이 좋은 조합은 ccp_alpha=0.02, max_depth=8, min_samples_leaf=5로 선택되었다. 이는 트리의 복잡도를 무제한으로 두지 않고(최대 깊이 8), 말단 노드가 너무 작은 표본(최소 5개 미만)에 의해 결정되지 않도록 제한함으로써 예측의 분산을 낮추려는 설정이다.

또한 ccp_alpha=0.02는 비용-복잡도 가지치기를 적용해 불필요한 잔가지를 제거하는 수준의 규제를 의미하며, 훈련 데이터에 과도하게 맞추는 과적합을 완화하고 일반화 성능을 높이는 방향으로 작동한다. 이 최적 설정으로 학습된 모델은 테스트셋에서 RMSE 약 2.84, MAE 약 2.08, R² 약 0.84를 기록하여, 단일 회귀나무임에도 비교적 안정적인 예측력을 보였다.

Best params: {'tree__ccp_alpha': 0.02, 'tree__max_depth': 8, 'tree__min_samples_leaf': 5} | Test RMSE: 2.838844476667391 | Test MAE: 2.0839359849011747 | Test R^2: 0.8421052924722378

회귀결정나무

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

tree_model = best_reg.named_steps["tree"]
feature_names = best_reg.named_steps["prep"].get_feature_names_out()
feature_names = [s.replace("cat__", "").replace("num__", "") for s in feature_names]

plt.figure(figsize=(28, 12), dpi=200)
plot_tree(tree_model, feature_names=feature_names,
          filled=True, rounded=True, max_depth=3, fontsize=10, precision=2)
plt.tight_layout()
plt.show()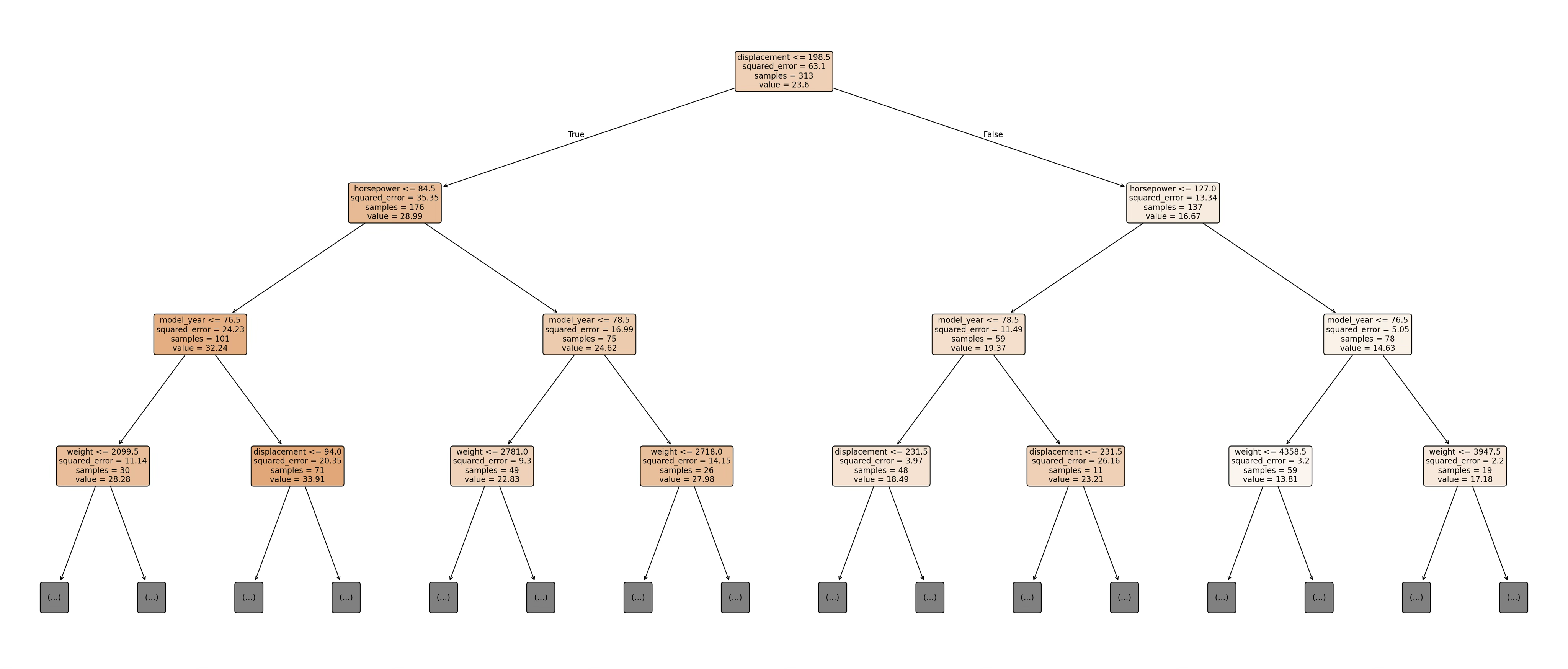

회귀결정 절차 출력

from sklearn.tree import export_text

print(export_text(tree_model, feature_names=list(feature_names), decimals=2))

배기량이 작고(≤198.5), 마력이 낮으며(≤84.5), 1976년 이전 모델 중에서 가벼운 차(≤2099.5)라면, 일본산 차량은 평균 연비가 약 32.2mpg로, 일본산이 아닌 차량보다(약 28.9mpg) 더 높게 예측된다.

|--- displacement <= 198.50
| |--- horsepower <= 84.50
| | |--- model_year <= 76.50
| | | |--- weight <= 2099.50
| | | | |--- origin_japan <= 0.50
| | | | | |--- value: [28.93]
| | | | |--- origin_japan > 0.50

예측변수 중요도

import pandas as pd
imp = pd.Series(tree_model.feature_importances_, index=feature_names).sort_values(ascending=False)
imp.head(15)

단일 회귀나무(DecisionTreeRegressor)의 변수 중요도(합은 1)는 하나의 결정나무에서 → 분할에 사용된 빈도 + 불순도 감소량을 기준으로 계산된다. 단일 회귀나무의 변수 중요도 분석 결과, 연비(mpg)는 배기량(displacement)에 의해 지배적으로 설명되며(65.3%), 이는 트리 구조가 상관된 변수 중 하나를 대표 변수로 선택하는 특성에 기인한다. 반면, 차량 중량이나 제조국과 같은 변수는 배기량 분기 이후 추가적인 오차 감소 기여가 제한되어 중요도가 낮게 나타났다.

변수	중요도(%)
displacement	0.653672
horsepower	0.148266
weight	0.119220
model_year	0.074448
acceleration	0.004394
origin_usa	0.000000
origin_europe	0.000000
origin_japan	0.000000

이상치 출력

err = (y_test - pred_test).abs()
top10_idx = err.sort_values(ascending=False).head(10).index

case_top10 = X_test.loc[top10_idx].copy()
case_top10["true_mpg"] = y_test.loc[top10_idx]
case_top10["pred_mpg"] = pred_test[[list(X_test.index).index(i) for i in top10_idx]]
case_top10["abs_error"] = err.loc[top10_idx]
case_top10

회귀나무 모형의 예측 결과를 바탕으로 테스트 자료에서 절대오차가 큰 관측치 상위 10개를 확인한 결과, 이상치는 주로 실제 연비(mpg)가 매우 높거나 낮은 차량에서 발생하는 경향을 보였다. 특히 실제 연비가 40mpg 이상으로 높은 일부 유럽산 소형 차량의 경우, 모형은 약 30mpg 내외로 예측하여 실제 값을 과소추정하였으며, 이로 인해 10mpg 이상의 큰 오차가 발생하였다.

이는 해당 차량들이 배기량, 중량, 마력 등의 주요 설명변수 측면에서는 유사한 집단에 속하지만, 실제로는 설계 효율이나 세부 기술 차이로 인해 평균적인 패턴을 벗어난 경우로 해석할 수 있다. 반대로 실제 연비가 낮은 일부 차량에 대해서는 모형이 상대적으로 높은 연비를 예측하는 사례도 관찰되었는데, 이는 회귀나무가 말단 노드에서 동일 조건을 만족하는 관측치들의 평균값을 예측값으로 사용하기 때문에, 극단적인 개별 사례의 특성이 충분히 반영되지 못한 결과로 볼 수 있다.

이러한 이상치 분석 결과는 본 모형이 전반적인 연비 구조를 안정적으로 설명하고 있음에도 불구하고, 평균적 규칙에서 벗어난 차량에 대해서는 예측 오차가 커질 수 있음을 보여주며, 회귀나무 기반 모형의 한계와 함께 추가적인 앙상블 모형(Random Forest 등)의 필요성을 시사한다.

displacement	horsepower	weight	acceleration	model_year	origin	true_mpg	pred_mpg	abs_error
97.0	52.0	2130	24.6	82	europe	44.0	33.500000	10.500000
70.0	90.0	2124	13.5	73	japan	18.0	26.940000	8.940000
267.0	125.0	3605	15.0	79	usa	19.2	26.340000	7.140000
232.0	90.0	3085	17.6	76	usa	22.5	16.500000	6.000000
91.0	69.0	2130	14.7	79	europe	37.3	42.900000	5.600000
225.0	105.0	3439	15.5	71	usa	16.0	20.623077	4.623077
134.0	95.0	2515	14.8	78	japan	21.1	25.642857	4.542857
232.0	112.0	2835	14.7	82	usa	22.0	26.340000	4.340000
120.0	88.0	2160	14.5	82	japan	36.0	31.840000	4.160000
97.0	75.0	2265	18.2	77	japan	26.0	30.100000	4.100000

앙상블 기법 비교

# [회귀-셀 1] 데이터 + (회귀) X, y + 전처리
import numpy as np
import pandas as pd
import seaborn as sns

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder

# 데이터
df = sns.load_dataset("mpg").dropna()

# 회귀 타깃/설명변수
y_r = df["mpg"]
X_r = df[["displacement", "horsepower", "weight", "acceleration", "model_year", "origin"]]

num_cols_r = ["displacement", "horsepower", "weight", "acceleration", "model_year"]
cat_cols_r = ["origin"]

# origin 원-핫(기본: sparse)
preprocess_r = ColumnTransformer(
    transformers=[
        ("cat", OneHotEncoder(handle_unknown="ignore"), cat_cols_r),
        ("num", "passthrough", num_cols_r),
    ]
)

# Boosting용(dense)
try:
    ohe_dense_r = OneHotEncoder(handle_unknown="ignore", sparse_output=False)  # sklearn 최신
except TypeError:
    ohe_dense_r = OneHotEncoder(handle_unknown="ignore", sparse=False)         # sklearn 구버전

preprocess_dense_r = ColumnTransformer(
    transformers=[
        ("cat", ohe_dense_r, cat_cols_r),
        ("num", "passthrough", num_cols_r),
    ]
)

#[회귀-셀 2] train/test 분할
from sklearn.model_selection import train_test_split

Xr_train, Xr_test, yr_train, yr_test = train_test_split(
    X_r, y_r, test_size=0.2, random_state=42
)

print("Train:", Xr_train.shape, "Test:", Xr_test.shape)

#[회귀-셀 3] 평가 함수(RMSE/MAE/R²)
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

def eval_reg(model, X_test, y_test):
    pred = model.predict(X_test)
    rmse = np.sqrt(mean_squared_error(y_test, pred))
    mae  = mean_absolute_error(y_test, pred)
    r2   = r2_score(y_test, pred)
    return {"RMSE": rmse, "MAE": mae, "R2": r2}

# [회귀-셀 4] 베이스라인(단일 회귀나무) + 앙상블 3~4종 학습/비교
from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor, RandomForestRegressor, AdaBoostRegressor, GradientBoostingRegressor

# (선택) best_reg가 없다면, 단순 baseline 트리 하나 생성
try:
    baseline_r = best_reg
except NameError:
    baseline_r = Pipeline([
        ("prep", preprocess_r),
        ("model", DecisionTreeRegressor(random_state=42, max_depth=8, min_samples_leaf=5))
    ])
    baseline_r.fit(Xr_train, yr_train)

# 버전 호환: Bagging/AdaBoost의 estimator 인자 처리
def make_bagging_reg():
    try:
        return BaggingRegressor(
            estimator=DecisionTreeRegressor(min_samples_leaf=5, random_state=42),
            n_estimators=300, max_samples=0.8, bootstrap=True, n_jobs=-1, random_state=42
        )
    except TypeError:
        return BaggingRegressor(
            base_estimator=DecisionTreeRegressor(min_samples_leaf=5, random_state=42),
            n_estimators=300, max_samples=0.8, bootstrap=True, n_jobs=-1, random_state=42
        )

def make_adaboost_reg():
    try:
        return AdaBoostRegressor(
            estimator=DecisionTreeRegressor(max_depth=3, random_state=42),
            n_estimators=300, learning_rate=0.05, random_state=42
        )
    except TypeError:
        return AdaBoostRegressor(
            base_estimator=DecisionTreeRegressor(max_depth=3, random_state=42),
            n_estimators=300, learning_rate=0.05, random_state=42
        )

# 1) Bagging
bag_r = Pipeline([
    ("prep", preprocess_r),
    ("model", make_bagging_reg())
])

# 2) Random Forest
rf_r = Pipeline([
    ("prep", preprocess_r),
    ("model", RandomForestRegressor(
        n_estimators=500, max_features="sqrt",
        min_samples_leaf=2, n_jobs=-1, random_state=42
    ))
])

# 3) Boosting - AdaBoost(회귀)
ada_r = Pipeline([
    ("prep", preprocess_dense_r),   # 안전하게 dense
    ("model", make_adaboost_reg())
])

# 4) Boosting - GradientBoosting(회귀)
gb_r = Pipeline([
    ("prep", preprocess_dense_r),   # ✅ dense 권장
    ("model", GradientBoostingRegressor(random_state=42))
])

# 학습
bag_r.fit(Xr_train, yr_train)
rf_r.fit(Xr_train, yr_train)
ada_r.fit(Xr_train, yr_train)
gb_r.fit(Xr_train, yr_train)

models_r = {
    "Tree(baseline)": baseline_r,
    "Bagging": bag_r,
    "RandomForest": rf_r,
    "AdaBoost": ada_r,
    "GradBoost": gb_r
}

rows = []
for name, m in models_r.items():
    rows.append({"Model": name, eval_reg(m, Xr_test, yr_test)})

result_reg = pd.DataFrame(rows).sort_values("RMSE")
result_reg

Model	RMSE	MAE	R2
Bagging	2.446737	1.786180	0.882711
GradBoost	2.543061	1.768160	0.873294
RandomForest	2.580404	1.818524	0.869545
AdaBoost	2.779743	2.105698	0.848611
Tree(baseline)	2.838844	2.083936	0.842105

# [회귀-셀 5] (선택) Random Forest 변수 중요도
rf_model = rf_r.named_steps["model"]
feat_names = rf_r.named_steps["prep"].get_feature_names_out()
feat_names = [s.replace("cat__", "").replace("num__", "") for s in feat_names]

pd.Series(rf_model.feature_importances_, index=feat_names).sort_values(ascending=False)

Random Forest 회귀모형의 변수 중요도(feature importance) 값의 합은 1이다. 각 값은 해당 변수가 예측 오차(RMSE 감소)에 기여한 상대적 비중을 의미하므로 Random Forest 회귀 결과, 연비(mpg)는 배기량·중량·마력 등 차량의 물리적 규모 변수가 전체 예측력의 약 74%를 설명하며, 연식 효과가 그 다음으로 중요하게 나타났다. 제조국 변수는 차량 특성이 이미 반영된 이후의 잔여 효과로 상대적으로 낮은 중요도를 보였다.

변수	중요도(%)
displacement	0.265666
weight	0.257668
horsepower	0.211913
model_year	0.132087
origin_usa	0.052645
acceleration	0.049994
origin_japan	0.025246
origin_europe	0.004781

# 예측 이상치 상위 10개

import numpy as np
import pandas as pd

# 1) Random Forest 예측 (테스트셋)
pred_rf = rf_r.predict(Xr_test)

# 2) 절대오차(이상치 점수)
err_rf = (yr_test - pred_rf).abs()

# 3) 오차 큰 상위 10개 인덱스
top10_idx_rf = err_rf.sort_values(ascending=False).head(10).index

# 4) 케이스 테이블(설명변수 + 실제/예측/오차)
case_top10_rf = Xr_test.loc[top10_idx_rf].copy()
case_top10_rf["true_mpg"] = yr_test.loc[top10_idx_rf]
case_top10_rf["pred_mpg"] = pd.Series(pred_rf, index=Xr_test.index).loc[top10_idx_rf]
case_top10_rf["abs_error"] = err_rf.loc[top10_idx_rf]

case_top10_rf

Random Forest 앙상블 모형의 예측 결과를 기준으로 절대오차가 큰 상위 10개 관측치를 살펴본 결과, 이상치는 주로 중·소형 차량이면서 실제 연비가 평균적인 패턴에서 크게 벗어난 사례에서 발생하였다.

특히 일본산 차량 중 배기량과 중량이 비교적 작음에도 불구하고 실제 연비가 낮은 차량의 경우, 모형은 동일한 조건의 평균적인 차량 특성을 반영하여 연비를 과대추정하는 경향을 보였으며, 이로 인해 9mpg 내외의 큰 예측 오차가 나타났다.

반대로 유럽산 차량 중 일부 고연비 차량의 경우에는 실제 연비가 40mpg 이상임에도 불구하고, 모형은 유사한 제원(배기량·중량·마력)을 가진 차량 집단의 평균값에 근거해 예측함으로써 실제 값을 과소추정하는 사례가 관찰되었다.

이러한 결과는 회귀나무 모형이 동일한 분기 조건에 속한 관측치들의 평균 연비를 예측값으로 사용하기 때문에, 설계 효율이나 기술적 특성으로 인해 평균적 경향에서 벗어난 차량에 대해서는 상대적으로 큰 오차가 발생할 수 있음을 보여준다. 즉, 본 이상치들은 데이터 오류라기보다는 평균적 규칙에 기반한 트리 모형의 구조적 한계를 반영한 사례로 해석할 수 있다.

displacement	horsepower	weight	acceleration	model_year	origin	true_mpg	pred_mpg	abs_error
70.0	90.0	2124	13.5	73	japan	18.0	27.061789	9.061789
97.0	52.0	2130	24.6	82	europe	44.0	36.166342	7.833658
90.0	75.0	2108	15.5	74	europe	24.0	29.744109	5.744109
225.0	85.0	3465	16.6	81	usa	17.6	23.155685	5.555685
122.0	88.0	2500	15.1	80	europe	35.0	29.570351	5.429649
134.0	95.0	2515	14.8	78	japan	21.1	26.486449	5.386449
140.0	90.0	2264	15.5	71	usa	28.0	23.117881	4.882119
79.0	67.0	1963	15.5	74	europe	26.0	30.758621	4.758621
120.0	88.0	2160	14.5	82	japan	36.0	31.902306	4.097694
91.0	70.0	1955	20.5	71	usa	26.0	29.847802	3.847802

회귀나무 모형의 예측 결과를 기준으로 절대오차가 큰 상위 10개 관측치를 살펴본 결과, 이상치는 주로 중·소형 차량이면서 실제 연비가 평균적인 패턴에서 크게 벗어난 사례에서 발생하였다. 특히 일본산 차량 중 배기량과 중량이 비교적 작음에도 불구하고 실제 연비가 낮은 차량의 경우, 모형은 동일한 조건의 평균적인 차량 특성을 반영하여 연비를 과대추정하는 경향을 보였으며, 이로 인해 9mpg 내외의 큰 예측 오차가 나타났다.

반대로 유럽산 차량 중 일부 고연비 차량의 경우에는 실제 연비가 40mpg 이상임에도 불구하고, 모형은 유사한 제원(배기량·중량·마력)을 가진 차량 집단의 평균값에 근거해 예측함으로써 실제 값을 과소추정하는 사례가 관찰되었다. 이러한 결과는 회귀나무 모형이 동일한 분기 조건에 속한 관측치들의 평균 연비를 예측값으로 사용하기 때문에, 설계 효율이나 기술적 특성으로 인해 평균적 경향에서 벗어난 차량에 대해서는 상대적으로 큰 오차가 발생할 수 있음을 보여준다. 즉, 본 이상치들은 데이터 오류라기보다는 평균적 규칙에 기반한 트리 모형의 구조적 한계를 반영한 사례로 해석할 수 있다.

(3) 분류가지

목표변수 mpg 범주화

import numpy as np
import pandas as pd
import seaborn as sns

# 0) 데이터
df = sns.load_dataset("mpg").dropna()

# 1) 분류 타깃: mpg >= 25 → High, else Low
mpg_level = 25
df["mpg_class"] = np.where(df["mpg"] >= mpg_level, "High", "Low")

print(df["mpg_class"].value_counts())

전체 392대의 차량 중에서 저연비(Low)로 분류된 차량이 226대, 고연비(High)로 분류된 차량이 166대로 나타났다. 이는 연비 기준값을 25mpg로 설정했을 때, 저연비 차량의 비중이 약 57.7%, 고연비 차량의 비중이 약 42.3%임을 의미한다.

mpg_class
Low 226
High 166

분류나무 예측

# 목표변수, 예측변수 선정

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder

# y(목표)
y = df["mpg_class"]

# X(설명변수)  ※ mpg는 타깃 생성에 사용되었으므로 제외하는 것이 타당함
X = df[["displacement", "horsepower", "weight", "acceleration", "model_year", "origin"]]

num_cols = ["displacement", "horsepower", "weight", "acceleration", "model_year"]
cat_cols = ["origin"]

preprocess = ColumnTransformer(
    transformers=[
        ("cat", OneHotEncoder(handle_unknown="ignore"), cat_cols),
        ("num", "passthrough", num_cols),
    ]
)

# 데이터 분할 (훈련, 테스트) 
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y,
    test_size=0.2,
    random_state=42,
    stratify=y   # ✅ 클래스 비율 유지
)

분류나무 예측 결과 정확성 통계량

from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV

pipe = Pipeline([
    ("prep", preprocess),
    ("tree", DecisionTreeClassifier(random_state=42))
])

param_grid = {
    "tree__max_depth": [2, 3, 4, 5, 8, None],
    "tree__min_samples_leaf": [1, 3, 5, 10, 20],
    "tree__ccp_alpha": [0.0, 0.001, 0.005, 0.01, 0.02]
}

gs_clf = GridSearchCV(
    pipe,
    param_grid=param_grid,
    cv=5,
    scoring="f1_macro",  # ✅ 불균형(226 vs 166) 고려
    n_jobs=-1
)
gs_clf.fit(X_train, y_train)

best_clf = gs_clf.best_estimator_
print("Best params:", gs_clf.best_params_)
print("Best CV f1_macro:", gs_clf.best_score_)

분류나무 모형에 대해 GridSearchCV를 이용하여 하이퍼파라미터를 교차검증 기준으로 탐색한 결과, 최대 트리 깊이 8, 리프 노드의 최소 표본 수 5, 그리고 비용-복잡도 가지치기 계수(ccp_alpha)를 적용하지 않은 조합(ccp_alpha=0.0)이 최적의 모형으로 선택되었다.

이는 본 데이터에서 분류 문제의 핵심 구조가 비교적 명확하여, 추가적인 가지치기를 적용할 경우 오히려 클래스 구분에 필요한 정보가 손실될 수 있음을 시사한다. 특히 리프 노드 최소 표본 수를 5로 제한함으로써 극소수 관측치에 기반한 불안정한 규칙 생성을 방지하는 동시에, 최대 깊이를 8까지 허용하여 연비 수준(고·저)을 구분하는 데 필요한 비선형적 의사결정 구조를 충분히 반영하도록 설정된 것으로 해석할 수 있다.

이와 같은 설정에서 교차검증 기준 macro F1-score가 약 0.88로 나타났는데, 이는 저연비와 고연비 차량 간 표본 수가 다소 차이를 보이는 상황에서도 두 클래스를 비교적 균형 있게 분류하고 있음을 의미한다. 따라서 본 분류나무 모형은 단순한 정확도 중심 분류를 넘어, 클래스 불균형을 고려한 안정적인 분류 성능을 확보한 모형으로 평가할 수 있다.

Best params: {'tree__ccp_alpha': 0.0, 'tree__max_depth': 8, 'tree__min_samples_leaf': 5}
Best CV f1_macro: 0.8800101889457143

분류나무 예측 Confusion matrix

# 예측 Confusion 
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

pred_test = best_clf.predict(X_test)
proba_test = best_clf.predict_proba(X_test)
classes = list(best_clf.classes_)

acc = accuracy_score(y_test, pred_test)
print("Test Accuracy:", acc)
print(classification_report(y_test, pred_test))

cm = confusion_matrix(y_test, pred_test, labels=classes)
print("Classes:", classes)
print("Confusion matrix (rows=True, cols=Pred):\n", cm)

테스트셋(79개 관측치)에서 분류나무 모형의 정확도는 0.873으로, 전체 79개 중 69개를 올바르게 분류하였다. 클래스별 성능을 보면 고연비(High)는 재현율이 0.91로 높아 실제 High 33개 중 30개를 정확히 High로 찾아냈으며, 정밀도는 0.81로 나타나 High로 예측한 사례 중 일부가 실제로는 Low였음을 의미한다.

반면 저연비(Low)는 정밀도 0.93으로 Low라고 예측한 경우의 신뢰도는 높지만, 재현율이 0.85로 실제 Low 46개 중 39개만 정확히 Low로 분류되어 일부 Low를 High로 놓치는(=High로 잘못 분류하는) 경향이 관찰된다.

혼동행렬을 기준으로 보면 실제 High 33개 중 3개가 Low로 오분류(High→Low)되었고, 실제 Low 46개 중 7개가 High로 오분류(Low→High)되었다. 즉, 본 모형은 전반적으로 균형 잡힌 성능을 보이되, 상대적으로 ’저연비 차량을 고연비로 과대분류(Low→High)’하는 오류가 더 많이 발생하는 구조를 가진다고 해석할 수 있다. 이때 macro F1-score가 0.87로 나타난 것은 클래스별 성능을 평균적으로 고려했을 때도 분류 성능이 양호함을 시사한다.

Test Accuracy: 0.8734177215189873
precision recall f1-score support
High 0.81 0.91 0.86 33
Low 0.93 0.85 0.89 46
accuracy 0.87 79
macro avg 0.87 0.88 0.87 79
weighted avg 0.88 0.87 0.87 79

Classes: ['High', 'Low']
Confusion matrix (rows=True, cols=Pred):
[[30 3]
[ 7 39]]

의사결정 트리 출력

# 의사결정 트리
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

tree_model = best_clf.named_steps["tree"]
feature_names = best_clf.named_steps["prep"].get_feature_names_out()
feature_names = [s.replace("cat__", "").replace("num__", "") for s in feature_names]

plt.figure(figsize=(28, 12), dpi=200)
plot_tree(
    tree_model,
    feature_names=feature_names,
    class_names=classes,
    filled=True, rounded=True,
    max_depth=3,
    fontsize=10,
    precision=2
)
plt.tight_layout()
plt.show()

오분류 10건을 유형별로 보면, 실제 고연비(High)를 저연비(Low)로 분류한 경우(High→Low)는 3건, 실제 저연비(Low)를 고연비(High)로 분류한 경우(Low→High)는 7건으로 나타나 ’저연비를 고연비로 과대분류’하는 오류가 더 많이 발생하였다. 이는 혼동행렬 [[30, 3], [7, 39]](행=실제, 열=예측)에서 확인되며, 분류나무의 규칙 구조가 특정 경계 구간에서 High 쪽으로 판단을 밀어주는 구간이 존재함을 시사한다.

먼저 High→Low(3건) 과소추정형 오류는, 실제로는 고연비임에도 불구하고 트리 규칙상 Low로 강하게 귀결되는 조건(예: 배기량이 크거나(displacement > 190.5) 특정 연식 이하(model_year ≤ 80.5)로 묶이는 구간)에 포함될 때 발생한다. 해당 구간은 트리 출력에서 displacement > 190.5인 경우가 거의 전부 Low로 결정되도록 설계되어 있어(”|--- displacement > 190.50 … class: Low”), 실제 mpg가 25 이상인 예외적 차량이 이 구간에 들어오면 High임에도 Low로 떨어질 가능성이 커진다. 즉, ’큰 배기량·특정 연식’ 조합에서는 평균적으로 저연비가 지배적이기 때문에, 소수의 고연비 예외 사례가 트리의 평균적 규칙에 의해 Low로 흡수되는 형태의 과소추정형 오분류가 나타난다.

반대로 Low→High(7건) 과대추정형 오류는, 실제로는 저연비임에도 불구하고 트리가 High로 판단하는 조건 경로에 들어갈 때 발생한다. 예컨대 displacement ≤ 190.5이면서 horsepower ≤ 93.5인 구간에서, (1) model_year가 73.5 이하이고 weight가 2204.5 이하인 경우, 혹은 (2) model_year가 73.5 초과이고 weight ≤ 2737.5인 경우 등은 트리 규칙상 High로 분류되는 경향이 강하다(출력 규칙에서 해당 분기들이 반복적으로 ”class: High”로 귀결). 이때 실제로는 연비가 낮은 차량이 이러한 ’상대적으로 작은 배기량·낮은 마력·가벼운 차체’ 조건에 포함되면, 트리는 평균적 패턴에 근거해 High로 판단해 버려 Low→High 오분류가 발생한다. 즉, 저연비인데도 외형적 제원(배기량·마력·중량)이 고연비 집단과 유사한 ’경계형 차량’들이 High 쪽으로 잘못 끌려가는 것이 과대추정형 오류의 주요 원인이다.

종합하면, High→Low 오분류는 ’대배기량(또는 특정 조건) 구간에서 거의 모두 Low로 결정되는 강한 규칙’ 때문에 발생하는 예외 사례의 흡수 현상으로 이해할 수 있고, Low→High 오분류는 ’소배기량·저마력·경량’ 조건에서 High로 분류하는 평균적 규칙이 경계형 저연비 차량을 High로 끌어올리는 결과로 해석할 수 있다. 따라서 본 분류나무의 오분류는 단순한 우연이라기보다, 트리가 학습한 조건부 평균적 패턴과 경계 구간의 예외 사례가 충돌하면서 나타나는 구조적 결과로 평가할 수 있다.

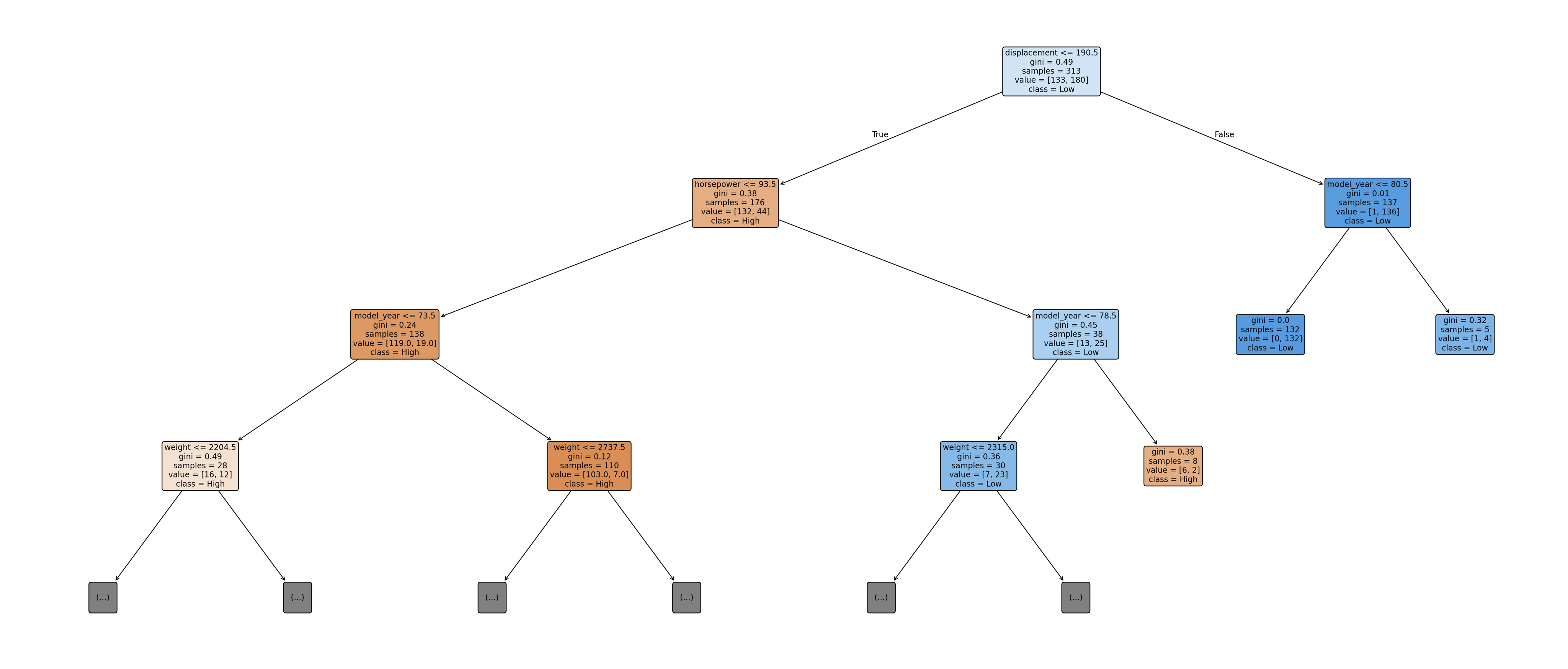
의사결정 절차

#의사결정 절차 출력
from sklearn.tree import export_text

print(export_text(tree_model, feature_names=list(feature_names), decimals=2))

이 분기 규칙은 배기량이 190.5 이하이고 마력이 93.5 이하이며 연식이 73.5 이하인 차량들 가운데, 차량 중량이 2204.5 이하로 가벼운 경우에는 고연비(High)로 일관되게 분류하는 반면, 중량이 그보다 무거운 경우에는 마력 86.5를 기준으로 저연비(Low)와 고연비(High)를 다시 구분하도록 설계되어 있음을 의미한다.

Low→High(과대추정형) 오분류 사례는 대체로 배기량이 190.5 이하이고 마력이 93.5 이하이며, 연식이 1973년 이전인 조건 경로에 포함된 차량에서 발생한다. 이 경로에서는 차량 중량이 2204.5 이하인 경우 추가 조건과 무관하게 고연비(High)로 분류되는 규칙이 작동한다. 실제로 일부 저연비 차량은 외형적 제원(소배기량·저마력·경량)이 고연비 집단과 유사하여 해당 리프 노드에 포함되지만, 엔진 효율이나 설계 특성으로 인해 실제 연비는 25mpg 미만에 머무른다. 그 결과, 트리는 해당 차량을 평균적 패턴에 따라 High로 판단하여 저연비 차량을 고연비로 과대추정하는 오분류가 발생한다.

반대로 High→Low(과소추정형) 오분류 사례는 배기량이 190.5를 초과하거나, 또는 배기량이 작더라도 중량이 2204.5를 초과하면서 마력이 86.5 이하인 조건 경로에서 주로 관찰된다. 이 구간은 학습 데이터에서 저연비 차량이 다수를 차지하여 Low로 귀결되는 강한 규칙이 형성되어 있으며, 실제 연비가 25mpg 이상인 예외적 차량이라 하더라도 동일 경로에 포함되면 저연비로 분류된다. 즉, 평균적으로 연비가 낮은 조건 구간에 소수의 고연비 차량이 포함될 경우, 분류나무의 조건부 다수결 구조에 의해 고연비 차량이 저연비로 흡수되는 과소추정형 오분류가 발생한다.

종합하면, Low→High 오분류는 ’경량·저출력’이라는 평균적 고연비 규칙이 경계형 저연비 차량을 High로 끌어올리는 현상이며, High→Low 오분류는 ’중량 증가 또는 대배기량’ 구간에서 형성된 강한 저연비 규칙이 고연비 예외 사례를 Low로 눌러버리는 현상으로 해석할 수 있다. 이는 분류나무가 개별 관측치의 특성보다는 해당 규칙 경로에 속한 집단의 지배적 패턴에 따라 판단을 내리는 구조적 특성을 반영한 결과이다.

|--- displacement <= 190.50
| |--- horsepower <= 93.50
| | |--- model_year <= 73.50
| | | |--- weight <= 2204.50
| | | | |--- weight <= 2123.50
| | | | | |--- class: High
| | | | |--- weight > 2123.50
| | | | | |--- class: High
| | | |--- weight > 2204.50
| | | | |--- horsepower <= 86.50
| | | | | |--- class: Low
| | | | |--- horsepower > 86.50
| | | | | |--- class: High

해당 분기 규칙은 배기량이 190.5 이하이고 마력이 93.5 이하이며 연식이 1973년 이전인 차량 집단을 대상으로, 차량 중량(weight)을 핵심 기준으로 연비 등급을 판단하는 구조임을 보여준다. 이 조건 하에서 중량이 2204.5 이하인 경우에는 추가적인 세부 조건과 무관하게 모두 고연비(High)로 분류되는데, 이는 소배기량·저마력·경량 차량이 전반적으로 높은 연비를 보였다는 학습 데이터의 평균적 특성이 반영된 결과로 해석할 수 있다. 반면 중량이 2204.5를 초과하는 경우에는 동일한 제원 조건에서도 연비 성능의 이질성이 커지므로, 마력 86.5를 기준으로 다시 분기하여 저연비(Low)와 고연비(High)를 구분한다. 즉, 이 규칙은 ”경량 여부가 우선적으로 연비를 결정하고, 일정 수준 이상 무거워질 경우에는 마력 차이가 추가적인 구분 요인으로 작용한다”는 트리의 조건부 판단 논리를 명확히 드러낸다. 이러한 구조는 경량이지만 실제 연비가 낮은 일부 차량을 고연비로 과대분류(Low→High)하게 만드는 잠재적 원인이 되며, 동시에 평균적 규칙에 기반한 분류나무의 특성을 잘 보여주는 사례로 이해할 수 있다.

예측변수 중요도

import pandas as pd

imp = pd.Series(tree_model.feature_importances_, index=feature_names).sort_values(ascending=False)
imp

회귀나무 모형의 변수 중요도를 살펴보면, 연비(mpg) 예측에서 배기량(displacement)이 전체 중요도의 약 65.4%를 차지하며 압도적으로 가장 중요한 변수로 나타났다. 이는 본 모형이 연비를 설명하는 과정에서 배기량을 핵심적인 기준 변수로 활용하고 있음을 의미하며, 실제로 트리의 상위 분기에서 배기량이 반복적으로 사용된 결과로 해석할 수 있다. 그 다음으로는 마력(horsepower)과 차량 중량(weight)이 각각 약 14.8%, 11.9%의 중요도를 보이며, 배기량 다음으로 연비 변동을 설명하는 보조적인 역할을 수행한다. 반면 연식(model_year)의 중요도는 약 7.4%로 상대적으로 낮게 나타났는데, 이는 기술 발전에 따른 연비 개선 효과가 존재하더라도, 엔진 규모나 출력과 같은 물리적 특성에 비해 설명력이 제한적임을 시사한다. 한편 가속력(acceleration)은 중요도가 매우 낮아 연비 예측에 거의 기여하지 않는 것으로 나타났으며, 제조국(origin) 더미 변수들은 본 회귀나무 모형에서 분기에 사용되지 않아 중요도가 0으로 계산되었다. 이는 단일 회귀나무가 상관성이 높은 변수들 중 일부 대표 변수(배기량, 마력, 중량)를 선택해 설명력을 독점적으로 흡수하는 구조적 특성에 기인한 결과로 해석할 수 있다.

변수	중요도(%)
displacement	0.653672
horsepower	0.148266
weight	0.119220
model_year	0.074448
acceleration	0.004394
origin_usa	0.000000
origin_europe	0.000000
origin_japan	0.000000

import numpy as np
import pandas as pd

# 오분류 여부
wrong = (pred_test != y_test.values)

# High 확률(참고용)
idx_high = classes.index("High")
p_high = proba_test[:, idx_high]

res = X_test.copy()
res["true"] = y_test.values
res["pred"] = pred_test
res["p_high"] = p_high
res["correct"] = ~wrong
res["mpg"] = df.loc[res.index, "mpg"].values  # 실제 mpg도 같이 보기

# 오분류 중에서도 확신(확률)이 큰 케이스 우선 확인
res[res["correct"] == False].sort_values("p_high", ascending=False)

제시된 표는 테스트셋에서 분류나무가 오분류한 10개 관측치를 모아 놓은 결과로, 각 행은 한 차량(관측치)의 제원과 실제/예측 클래스, 그리고 예측 확률을 함께 보여준다.

true는 실제 연비 등급(기준: mpg≥25이면 High, 아니면 Low)이고, pred는 모형이 예측한 등급이며, p_high는 해당 차량이 High일 확률(모형의 예측확률)을 의미한다. correct=False는 실제와 예측이 불일치하는 오분류 사례임을 뜻한다.

오분류는 두 유형으로 나뉜다. 먼저 147, 209, 168, 334, 119, 78, 60번은 실제는 Low인데 예측을 High로 한 과대추정형(Low→High) 오분류이며, 특히 147과 209는 p_high=1.0으로 모형이 High라고 ”확신”했음에도 실제 mpg가 각각 24.0, 19.0으로 기준(25mpg) 아래에 있어 오분류가 발생한 사례다.

이들은 배기량·마력·중량 등의 제원 조합이 고연비 집단과 유사한 형태로 나타나 트리 규칙상 High 쪽 리프 노드에 포함되었지만, 실제 연비는 임계값 미만이어서 Low로 판정되어야 했던 ’경계형/예외형’ 관측치로 해석할 수 있다. 특히 147(24.0), 168(23.0), 334(23.7)처럼 25mpg에 근접한 값들은 작은 제원 변화나 규칙 경계에 의해 분류가 쉽게 뒤집히는 전형적인 사례다.

반대로 392, 327, 387번은 실제는 High인데 예측을 Low로 한 과소추정형(High→Low) 오분류이다. 이들 중 392는 실제 mpg가 27.0으로 High이지만 p_high=0.375로 모형은 High일 가능성을 낮게 보고 Low로 분류했으며, 327(실제 36.4)과 387(실제 38.0)은 실제 mpg가 매우 높음에도 불구하고 Low로 분류되었다.

특히 387은 배기량 262로 상대적으로 크기 때문에, 트리의 상위 규칙(예: displacement가 큰 구간은 대체로 Low)에서 Low로 강하게 귀결될 가능성이 크며, 그 결과 고연비 예외 사례가 평균적 규칙에 의해 Low로 ’눌리는’ 형태의 오분류가 발생한 것으로 해석할 수 있다.

종합하면, 본 오분류 표는 분류나무가 학습한 평균적 규칙(제원 기반 패턴)이 경계값 주변 차량(예: mpg≈25)이나 예외적 효율을 가진 차량(특히 고연비인데 제원이 ’저연비처럼’ 보이거나, 반대로 저연비인데 ’고연비처럼’ 보이는 경우)을 완전히 분리하지 못할 때 오분류가 발생한다는 점을 보여준다.

또한 p_high 값이 1.0에 가까운 오분류가 존재한다는 사실은, 단일 트리의 규칙이 특정 구간에서 지나치게 단정적(decisive)일 수 있음을 시사하며, 이를 완화하기 위해 Bagging/Random Forest와 같은 앙상블을 적용하면 경계 구간의 판단이 더 안정화될 가능성이 크다.

displacement	horsepower	weight	acceleration	model_year	origin	1	pred	p_high	correct	mpg
147	90.0	75.0	2108	15.5	74	europe	Low	High	1.000000	0	24.0
209	120.0	88.0	3270	21.9	76	europe	Low	High	1.000000	0	19.0
168	140.0	83.0	2639	17.0	75	usa	Low	High	0.888889	0	23.0
334	70.0	100.0	2420	12.5	80	japan	Low	High	0.750000	0	23.7
119	114.0	91.0	2582	14.0	73	europe	Low	High	0.600000	0	20.0
78	120.0	87.0	2979	19.5	72	europe	Low	High	0.600000	0	21.0
60	140.0	90.0	2408	19.5	72	usa	Low	High	0.600000	0	20.0
392	151.0	90.0	2950	17.3	82	usa	High	Low	0.375000	0	27.0
327	121.0	67.0	2950	19.9	80	europe	High	Low	0.375000	0	36.4
387	262.0	85.0	3015	17.0	82	usa	High	Low	0.200000	0	38.0

분류나무 + 앙상블

import numpy as np
import pandas as pd

from sklearn.metrics import (
    accuracy_score, f1_score, balanced_accuracy_score,
    confusion_matrix, classification_report, roc_auc_score
)
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder

# (1) 평가 함수
def eval_clf(model, X_test, y_test, pos_label="High"):
    pred = model.predict(X_test)

    out = {
        "Accuracy": accuracy_score(y_test, pred),
        "BalancedAcc": balanced_accuracy_score(y_test, pred),
        "F1(macro)": f1_score(y_test, pred, average="macro"),
        "F1(High)": f1_score(y_test, pred, pos_label=pos_label)
    }

    # ROC-AUC (predict_proba가 있을 때만)
    if hasattr(model, "predict_proba"):
        proba = model.predict_proba(X_test)
        classes = list(model.classes_)
        if pos_label in classes:
            p_pos = proba[:, classes.index(pos_label)]
            y_bin = (y_test == pos_label).astype(int)
            out["ROC-AUC"] = roc_auc_score(y_bin, p_pos)
        else:
            out["ROC-AUC"] = np.nan
    else:
        out["ROC-AUC"] = np.nan

    return out

# (2) Boosting(GradientBoosting)용: OneHot을 dense로 내보내는 전처리
try:
    ohe_dense = OneHotEncoder(handle_unknown="ignore", sparse_output=False)  # sklearn 최신
except TypeError:
    ohe_dense = OneHotEncoder(handle_unknown="ignore", sparse=False)         # sklearn 구버전

preprocess_dense = ColumnTransformer(
    transformers=[
        ("cat", ohe_dense, cat_cols),
        ("num", "passthrough", num_cols),
    ]
)

from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier

# 0) 베이스라인(지금 이미 best_clf가 있음) - 없으면 아래 주석 해제해서 만들 수도 있음
baseline = best_clf

# 1) Bagging (base tree는 너무 깊지 않게 두는 게 보통 안정적)
bag = Pipeline([
    ("prep", preprocess),
    ("model", BaggingClassifier(
        estimator=DecisionTreeClassifier(max_depth=None, min_samples_leaf=5, random_state=42),
        n_estimators=300,
        max_samples=0.8,
        bootstrap=True,
        n_jobs=-1,
        random_state=42
    ))
])

# 2) Random Forest
rf = Pipeline([
    ("prep", preprocess),
    ("model", RandomForestClassifier(
        n_estimators=500,
        max_features="sqrt",
        min_samples_leaf=2,
        n_jobs=-1,
        random_state=42
    ))
])

# 3) Boosting - AdaBoost (약한 트리(stump) 기반)
ada = Pipeline([
    ("prep", preprocess),
    ("model", AdaBoostClassifier(
        estimator=DecisionTreeClassifier(max_depth=1, random_state=42),
        n_estimators=300,
        learning_rate=0.05,
        random_state=42
    ))
])

# 4) Boosting - GradientBoosting (dense 전처리 사용 권장)
gb = Pipeline([
    ("prep", preprocess_dense),
    ("model", GradientBoostingClassifier(random_state=42)
    )
])

# 학습
bag.fit(X_train, y_train)
rf.fit(X_train, y_train)
ada.fit(X_train, y_train)
gb.fit(X_train, y_train)

# 성능 비교 테이블
models = {
    "Tree(baseline)": baseline,
    "Bagging": bag,
    "RandomForest": rf,
    "AdaBoost": ada,
    "GradBoost": gb
}

rows = []
for name, m in models.items():
    rows.append({"Model": name, eval_clf(m, X_test, y_test)})

result_df = pd.DataFrame(rows).sort_values("F1(macro)", ascending=False)
result_df

분류 성능 비교 결과를 보면, 단일 분류나무(Tree baseline)는 Accuracy 0.873, Balanced Accuracy 0.878, F1(macro) 0.872로 기본 성능을 보였으나, 앙상블 적용 시 전반적인 성능이 뚜렷하게 향상되었다. 특히 Bagging과 AdaBoost는 Accuracy가 0.937로 가장 높았고, Balanced Accuracy도 0.941로 나타나 두 클래스(High/Low)를 비교적 균형 있게 잘 구분하는 것으로 평가된다.

또한 F1(macro) 역시 0.936으로 가장 높아, 클래스 불균형을 고려한 종합 분류 성능 측면에서 가장 우수한 모델군으로 해석할 수 있다. Random Forest는 Accuracy 0.924, F1(macro) 0.923으로 Bagging/AdaBoost보다는 소폭 낮지만 여전히 단일 트리 대비 크게 개선된 성능을 보였다.

Gradient Boosting은 Accuracy 0.899, F1(macro) 0.897로 앙상블 중에서는 가장 낮았으나, baseline 트리보다는 확실히 높은 성능을 기록하였다. 한편 ROC-AUC는 Gradient Boosting이 0.974로 가장 높고 Bagging(0.970)과 Random Forest(0.970)도 매우 높은 수준을 보였는데, 이는 ’임계값을 바꿔가며’ High를 판별하는 능력(순위화 능력)은 부스팅 계열이 특히 강할 수 있음을 시사한다.

종합하면, 본 데이터에서는 최종 분류(라벨) 성능 기준으로는 Bagging/AdaBoost가 가장 우수하고, 확률 기반 판별력(ROC-AUC) 관점에서는 Gradient Boosting이 가장 강한 모델로 해석할 수 있다.

Model	Accuracy	BalancedAcc	F1(macro)	F1(High)	ROC-AUC
Bagging	0.936709	0.941370	0.935678	0.927536	0.970356
AdaBoost	0.936709	0.941370	0.935678	0.927536	0.963109
RandomForest	0.924051	0.926219	0.922549	0.911765	0.969697
GradBoost	0.898734	0.904480	0.897403	0.885714	0.974308
Tree(baseline)	0.873418	0.878458	0.871753	0.857143	0.952569

# 분류 Confusion Table
best_name = result_df.iloc[0]["Model"]
best_model = models[best_name]

print("Best model =", best_name)
pred = best_model.predict(X_test)

print(classification_report(y_test, pred))
print("Confusion matrix (rows=True, cols=Pred):")
print(confusion_matrix(y_test, pred, labels=["High","Low"]))

Bagging 분류모형을 테스트 자료(79개 관측치)에 적용한 결과, 전체 정확도는 0.94로 나타나 대부분의 차량을 올바르게 분류하고 있음을 확인할 수 있다. 고연비(High) 차량의 경우 재현율이 0.97로 매우 높아 실제 고연비 차량 33대 중 32대를 정확히 식별하였으며, 정밀도는 0.89로 나타나 고연비로 예측된 차량 중 일부(1대)는 실제로 저연비였음을 의미한다.

반면 저연비(Low) 차량은 정밀도가 0.98로 매우 높아 저연비로 예측된 결과의 신뢰도가 높았으며, 재현율은 0.91로 실제 저연비 차량 46대 중 42대를 정확히 분류하였다. 혼동행렬을 보면 실제 고연비 차량은 1건만 저연비로 오분류되었고(High→Low), 실제 저연비 차량은 4건이 고연비로 오분류(Low→High)되어, 전체 오분류는 5건에 불과하다.

이러한 결과는 Bagging 모형이 단일 분류나무에서 나타났던 경계 구간의 불안정성을 효과적으로 완화하여, 두 클래스 모두에서 균형 잡힌 분류 성능을 달성했음을 보여주며, 특히 고연비 차량을 놓치지 않는 방향으로 매우 안정적인 분류 성능을 보인다고 해석할 수 있다.

Best model = Bagging
precision recall f1-score support
High 0.89 0.97 0.93 33
Low 0.98 0.91 0.94 46
accuracy 0.94 79
macro avg 0.93 0.94 0.94 79
weighted avg 0.94 0.94 0.94 79

Confusion matrix (rows=True, cols=Pred):
[[32 1]
[ 4 42]]

# RF 파이프에서 모델 꺼내기
rf_model = rf.named_steps["model"]

# 전처리 후 변수명
feat_names = rf.named_steps["prep"].get_feature_names_out()
feat_names = [s.replace("cat__", "").replace("num__", "") for s in feat_names]

imp = pd.Series(rf_model.feature_importances_, index=feat_names).sort_values(ascending=False)
imp

제시된 결과는 앙상블 기반 트리 모형(예: Random Forest 또는 Bagging 계열)에서 산출된 변수 중요도로, 각 값은 전체 예측 성능에 대한 상대적 기여도를 의미한다.

가장 중요한 변수는 배기량(displacement, 0.27)과 차량 중량(weight, 0.27)으로, 두 변수가 거의 동일한 비중으로 전체 설명력의 절반 이상을 차지하고 있다. 이는 연비 수준(High/Low)을 구분하는 데 있어 차량의 물리적 크기와 무게가 가장 핵심적인 판단 기준임을 보여준다.

그 다음으로 마력(horsepower)이 0.20 수준의 중요도를 보여, 배기량·중량 다음의 주요 보조 변수로 작용하고 있다. 즉, 엔진 출력이 클수록 연비가 낮아질 가능성이 높다는 일반적인 자동차 공학적 특성이 모델에도 자연스럽게 반영된 것으로 해석할 수 있다. 연식(model_year)은 약 0.12의 중요도를 가지며, 기술 발전에 따른 연비 개선 효과를 일정 부분 설명하고 있으나, 엔진·차체 제원에 비해서는 상대적으로 영향력이 작다.

가속력(acceleration)은 0.06 수준으로 중요도가 낮은 편이며, 연비 분류에서는 보조적 역할에 그친다. 원산지(origin) 더미 변수들은 전체적으로 기여도가 크지 않지만, 그중에서는 미국(origin_usa)이 가장 높고(0.056), 일본과 유럽은 매우 낮은 값을 보인다. 이는 원산지 자체가 연비를 직접 결정하기보다는, 배기량·중량·마력 등 제원 차이를 통해 간접적으로 반영되고 있음을 시사한다.

종합하면, 이 변수 중요도 결과는 단일 트리에서 배기량에 과도하게 의존하던 구조가 앙상블을 통해 완화되어, 배기량·중량·마력이 비교적 균형 있게 연비 분류에 기여하고 있음을 보여준다. 즉, 앙상블 모형은 특정 변수 하나에 치우치기보다, 차량 제원의 종합적 패턴을 활용해 보다 안정적인 분류 규칙을 형성했다고 해석할 수 있다.

변수	중요도(%)
displacement	0.270001
weight	0.268190
horsepower	0.203223
model_year	0.121674
acceleration	0.059438
origin_usa	0.056267
origin_japan	0.013287
origin_europe	0.007921

# 이상치 상위 10개 출력
import pandas as pd
import numpy as np

# 예측
pred = best_model.predict(X_test)

# 확률(가능한 모델일 때)
proba = best_model.predict_proba(X_test)
classes = list(best_model.classes_)

# High 확률(참고용)
idx_high = classes.index("High")
p_high = proba[:, idx_high]

# 예측 확신도(예측 클래스의 최대확률)
conf = proba.max(axis=1)

res = X_test.copy()
res["true"] = y_test.values
res["pred"] = pred
res["p_high"] = p_high
res["confidence"] = conf
res["correct"] = (res["true"] == res["pred"])

# 오분류 확률 순 출력
res[res["correct"] == False].sort_values("confidence", ascending=False)

제시된 표는 Bagging 모형에서 오분류된 관측치 중 ’확신도(confidence)’가 높은 순서로 일부(5개)를 나열한 것이다. 각 행에서 true는 실제 등급, pred는 예측 등급이며, p_high는 High일 예측확률, confidence는 예측된 클래스의 최대확률(즉, 예측에 대한 확신도)을 의미한다. 따라서 pred=High인 경우에는 confidence가 사실상 p_high와 동일하게 나타나며, pred=Low인 경우에는 confidence가 (1−p_high)에 해당한다.

첫 번째 사례(147)는 실제는 Low(mpg<25)인데 예측은 High이며, p_high=0.995로 거의 1에 가까워 모형이 High라고 매우 강하게 확신했음에도 오분류가 발생했다. 이는 해당 차량(배기량 90, 마력 75, 중량 2108, 연식 74)이 전형적인 고연비 차량의 제원 패턴(소배기량·저출력·경량)에 매우 유사하여, Bagging이 다수의 트리에서 High로 일관되게 투표했기 때문으로 해석된다. 즉 실제 mpg는 임계값 아래에 있지만, 제원 기반 패턴은 High 쪽에 강하게 위치한 ’경계형/예외형’ 관측치이다.

두 번째 사례(387)는 실제는 High인데 예측은 Low이며, p_high=0.210으로 High일 확률을 낮게 보아 Low로 분류되었다(따라서 confidence=0.790). 이 차량은 배기량이 262로 큰 편이고 중량도 3015로 상당하여, 학습 데이터에서 주로 저연비로 나타나는 구간의 특성을 가진다. 그 결과 Bagging은 평균적 규칙에 따라 Low로 강하게 판단했으나, 실제 연비는 High인 ’고연비 예외’ 사례로 이해할 수 있다. 이는 고배기량·고중량 조건에서 드물게 나타나는 효율 좋은 차량이 앙상블에서도 일반 규칙에 의해 눌리는 전형적인 과소추정형(High→Low) 오분류에 해당한다.

세 번째(373), 네 번째(168), 다섯 번째(334)는 모두 실제 Low를 High로 예측한 과대추정형(Low→High) 오분류이며, 각각 p_high가 0.68~0.73 수준으로 비교적 높은 확신을 보인다. 이들 차량은 배기량이 아주 크지 않고(140 또는 70), 연식이 75~82로 상대적으로 신형이며, 중량도 극단적으로 무겁지 않은 편(2420~2865)이라 High 쪽 패턴과 겹치는 영역에 위치한다. 따라서 Bagging이 다수결로 High를 선택했지만, 실제 mpg는 기준치(25mpg) 미만이어서 Low가 정답인 사례로 해석된다. 특히 이런 유형은 ’제원 상 고연비처럼 보이지만 실제 연비가 낮은’ 차량들이며, 분류 임계값(25mpg) 근처에서 발생하는 경계 오분류일 가능성이 높다.

종합하면, 현재 출력된 오분류들은 (1) 소배기량·경량 패턴이 강해 실제 Low임에도 High로 강하게 분류되는 과대추정형, 그리고 (2) 고배기량·고중량이라는 평균적 저연비 규칙 때문에 실제 High가 Low로 떨어지는 과소추정형으로 구분된다. 또한 confidence가 매우 큰 오분류(예: 147, 387)의 존재는, Bagging이 단일 트리보다 안정적이지만 데이터 내 ’규칙을 깨는 예외 차량’에 대해서는 여전히 높은 확신을 가진 채 잘못 분류할 수 있음을 보여준다.

displacement	horsepower	weight	acceleration	model_year	origin	1	pred	p_high	confidence	correct
90.0	75.0	2108	15.5	74	europe	Low	High	0.995187	0.995187	0
262.0	85.0	3015	17.0	82	usa	High	Low	0.209535	0.790465	0
140.0	92.0	2865	16.4	82	usa	Low	High	0.726985	0.726985	0
140.0	83.0	2639	17.0	75	usa	Low	High	0.714420	0.714420	0
70.0	100.0	2420	12.5	80	japan	Low	High	0.680624	0.680624	0