Chapter 1. 다중공선성 개념
권세혁교수 통계 사전 【다중공선성】
shttps://sites.google.com/view/wolfpack61
다중공선성이란 독립변수들 간에 강한 선형관계가 존재하는 경우를 말한다. 회귀모형은 각 독립변수가 종속변수에 미치는 ”순수한 영향”을 추정하는 것을 목표로 한다. 그러나 독립변수끼리 강하게 상관되어 있으면 각 계수 추정치가 불안정해지고, 통계적 유의성이 왜곡될 수 있다.
1. 다중공선성이란?
다중 회귀모형에서 분석자가 가장 먼저 확인하는 것은 모형 전체가 목표변수를 잘 설명하는지에 대한 F-검정과, 각각의 예측변수가 독립적으로 의미 있는 역할을 하는지를 살펴보는 t-검정이다. 이러한 과정에서 자연스럽게 두 가지 관심사가 생긴다. 하나는 여러 예측변수 중에서 어떤 변수가 상대적으로 더 중요한가 하는 문제이고, 다른 하나는 각 변수가 목표변수에 구체적으로 어느 정도 영향을 미치는가 하는 문제이다.
상대적 중요성은 표준화 회귀계수를 통해 비교할 수 있으며, 목표변수에 대한 구체적 설명력은 OLS로 추정된 회귀계수를 통해 확인할 수 있다. 회귀계수의 의미는 단순하다. 다른 조건이 모두 동일할 때, 특정 예측변수가 한 단위 증가하면 목표변수는 그 계수 값만큼 변동한다는 것이다. 그러나 이런 해석은 다른 예측변수들이 변하지 않고 고정되어 있다는 전제가 필요하다. 만약 예측변수들 사이에 상관관계가 전혀 없다면, 각 회귀계수는 그 변수의 순수한 효과, 즉 주변효과를 그대로 보여주게 된다.
이처럼 회귀모형의 해석은 예측변수들 사이의 관계 구조에 크게 의존하며, 특히 예측변수들이 서로 강하게 연관되어 있을 때는 해석이 훨씬 복잡해진다.
현실의 데이터에서 예측변수들이 완벽하게 서로 독립인 경우는 거의 없다. 다만 예측변수들 간의 상관계수가 낮아 통계적으로 유의하지 않다면, 회귀계수의 해석은 여전히 타당하게 이루어질 수 있다. 반대로 예측변수들 간의 상관관계가 높아 통계적으로 유의하다면, 그때는 OLS로 얻은 회귀계수의 추정치와 분산 추정이 불안정해지고 검정 결과 역시 신뢰할 수 없게 된다. 이러한 상황을 다중공선성(multicollinearity) 문제라고 부른다.
예측변수들 사이에 높은 상관관계가 존재한다는 것은 곧 두 변수가 유사한 특성을 공유하고 있다는 뜻이며, 따라서 목표변수를 설명하는 역할에서도 상당 부분이 겹치게 된다. 원래 회귀분석에서 예측변수가 목표변수를 잘 설명한다는 것은 목표변수의 변동 방향을 정확하게 예측할 수 있음을 의미한다. 회귀계수가 양수라면 같은 방향으로, 음수라면 반대 방향으로 움직임을 포착한다는 것이다. 그런데 여러 예측변수가 동시에 목표변수와 강한 상관을 보인다면, 이들이 설명하는 변동 부분이 서로 중복되어 구분이 어려워진다. 이 때문에 다중공선성은 계수 해석을 혼란스럽게 만들고, 때로는 분석자가 의도한 해석을 무너뜨리기도 한다.
발생 원인
첫째는 구조적 다중공선성이다. 이는 연구자가 설정한 회귀모형 자체에서 비롯된다. 예를 들어 예측변수의 제곱항이나 곱항 같은 다항식 항을 포함하면, 원래 변수와 이들 변환 변수 사이에 강한 상관이 자연스럽게 발생한다. 이 경우 다중공선성은 데이터의 특성이 아니라 모형의 구조 때문에 나타난다.
둘째는 데이터 기반 다중공선성이다. 이는 실제 관측된 자료에서 예측변수들 간의 상관관계가 매우 높을 때 발생한다. 예컨대 소득과 소비, 교육수준과 소득처럼 현실적으로 밀접히 연관된 변수들을 동시에 포함하면 이들 간에 중복된 설명력이 생겨 다중공선성이 나타난다. 즉, 구조적 다중공선성은 모형 설계의 결과, 데이터 다중공선성은 자료의 속성에서 비롯된다고 정리할 수 있다.
2. 다중공선성 문제는 무엇인가?
예측변수(\(X_{k}\)) 간의 상관관계가 높으면(예: 두 설명변수의 상관관계가 높으면 (데이터 행렬의 한 열(변수)이 다른 열(변수와 상관계수가 큰 변수)로 표현되므로 \(det|X'X| \approx 0\) 되므로 \((X'X)^{- 1} = \frac{adj(X'X)}{det|X'X|}\)의 값이 매우 커진다. 이로 인하여 회귀계수 OLS 추정치 \(\widehat{\underset{¯}{b}} = (X'X)^{- 1}X'\underset{¯}{y}\) 값이 불안정해진다.
다중공선성 문제를 일으키지 않는 예측변수의 회귀계수에 비해 변동이 커진다. - 회귀모형의 작은 변화에도 회귀계수의 추정치는 매우 민감하게 반응한다.
그리고 OLS 추정의 추정분산(\(s^{2}(\widehat{\underset{¯}{b}}) = MSE(X'X)^{- 1}\)) 또한 매우 커져 회귀계수의 부호까지 바뀌는 문제가 발생한다.
회귀계수 추정 오차가 커지면 추정 정확도가 떨어지고 더 이상 회귀계수 유의성을 판단하는 유의확률(p-값)에 대한 신뢰성도 낮아진다. - 즉, 회귀계수 유의성 검정의 신뢰성 저하되어 추정 회귀모형 신뢰성 낮아진다.
3. 다중공선성 맛보기
보스톤 주택 가격(medv)의 예측변수 (lstat, indus, rm) 3개를 이용 다중공선성 문제를 살펴보자.
#피어슨 상관계수 boston[['medv','lstat','rm','ptratio']].corr(method ='pearson') |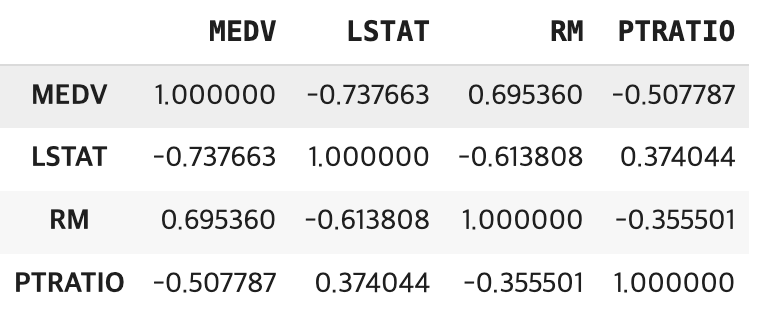
|
\[medv = 34.6 - 0.95*lstat,R^{2} = 54.4\%\]
먼저 lstat만 포함한 단순회귀모형에서는 회귀계수가 -0.95로 추정된다. 이는 저소득층 비율이 한 단위 증가할 때 주택가격이 평균적으로 약 0.95 단위 감소한다는 의미이며, 결정계수는 약 54.4%로 나타난다.
\[medv = - 1.36 - 0.64*lstat + 5.09*rm,R^{2} = 63.9\%\]
여기에 rm을 함께 넣으면 상황이 달라진다. lstat과 rm은 강한 상관관계를 갖는 변수인데, 두 변수를 동시에 포함하면 lstat의 회귀계수가 -0.64로 크게 줄어든다. 그 대신 rm의 회귀계수는 5.09로 추정되고, 결정계수는 63.9%로 상승한다. 즉, 두 변수가 설명하는 부분이 겹치면서 계수 값이 불안정해지고, 그 결과 단일변수 모형과 다변수 모형에서 해석이 달라지는 다중공선성의 전형적인 현상이 발생한다.
\[medv = 34.9 - 0.903*lstat - 0.08*indus,R^{2} = 54.6\%\]
반면 indus처럼 lstat과의 상관관계가 낮은 변수를 추가하면 다른 결과가 나온다. indus를 포함한 모형에서 lstat의 계수는 여전히 -0.9 수준으로 거의 변하지 않고, 결정계수 역시 54.6%로 단 0.2% 정도만 증가한다. 즉, 상관성이 낮은 변수를 추가하면 기존 변수의 계수에 큰 영향을 주지 않으며, 설명력도 크게 개선되지 않는다.
이 사례는 다중공선성이 주로 서로 상관관계가 큰 예측변수를 함께 투입할 때 발생한다는 점을 잘 보여준다. 목표변수를 설명하는 부분이 겹치기 때문에 회귀계수 값이 불안정해지고, 해석이 왜곡되거나 혼란스러워진다. 반대로 상관성이 낮은 변수를 포함할 때는 계수 해석이 비교적 안정적이다.
3. 다중공선성 문재 반드시 해결 해야 하나?
다중공선성 문제가 발생했다고 해서 반드시 그것을 제거하거나 해결해야 하는 것은 아니다. 다중공선성이 존재해도 회귀모형의 전체 예측력이나 적합도에는 큰 문제가 없기 때문이다. 실제로 목표변수를 예측하는 데 초점을 맞춘다면, 다중공선성이 있더라도 모형의 예측 성능은 크게 저하되지 않는다.
문제는 주로 해석 단계에서 나타난다. 다중공선성이 심할 경우, 회귀계수의 표준오차가 커져서 유의성이 불명확해지고, 계수의 크기나 부호가 직관에 어긋나게 추정될 수 있다. 따라서 ”어떤 예측변수가 목표변수에 더 큰 영향을 미치는가?“와 같은 변수별 효과 해석이 중요한 연구에서는 다중공선성을 무시하기 어렵다.
다중공선성이 반드시 해결해야 할 문제는 아니다. 특히 회귀모형에 통제변수가 포함된 경우, 다중공선성이 통제변수들에서만 발생하고 연구자가 관심을 두는 실험변수(주효과 변수)에서는 발생하지 않는다면, 굳이 제거하거나 수정할 필요가 없다.
실제로 Applied Linear Statistical Models (4판, p.289)에서도 언급하듯이, 예측변수들 사이에 일정 수준의 상관이 존재한다고 해서 모형의 적합 자체가 저해되거나 새로운 관측값에 대한 예측이 무의미해지는 것은 아니다. 다중공선성은 주로 개별 회귀계수의 해석과 검정에 영향을 미칠 뿐, 평균 반응(mean response)이나 예측값(prediction)의 정확성에는 큰 타격을 주지 않는다.
따라서 연구 목적이 ”주요 실험변수의 효과 검정”이라면, 통제변수들 사이의 다중공선성은 크게 문제 되지 않는다. 오히려 통제변수의 역할은 실험변수의 효과를 명확히 드러내는 데 있으므로, 약간의 공선성을 이유로 불필요하게 제거한다면 모형 해석이 왜곡될 수 있다.
이는 Baron & Kenny(1986)가 조절변수(moderator)와 매개변수(mediator) 모형을 제시할 때도 중요한 함의로 다루어졌다. 통제변수나 매개·조절변수는 본래 주요 변수의 관계를 보다 정교하게 설명하기 위해 포함되는 것이며, 이 과정에서 일부 상관관계가 존재하더라도 반드시 제거해야 하는 것은 아니라는 것이다.
즉, 실험변수에서 다중공선성이 없다면 문제 삼지 않아도 되며, 통제변수 사이의 공선성은 분석 목적상 자연스럽게 허용될 수 있다는 점이 핵심이다.
매개효과 Mediator
(순서1) \(y = a + b_{11}X + e\) : \(b_{11}\) 유의해야 한다.
(순서2) \(Me = a + b_{21}X + e\) : \(b_{21}\) 유의해야 한다.
(순서3) \(y = a + b_{31}X + b_{32}Me + e\) : \(b_{32}\) (매개효과) 유의하고 \(b_{31}\)은 \(b_{11}\)보다 절대값이 작아지거나 유의하지 않을 수 있음
조절효과 Moderate
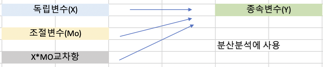
\[y = a + b_{1}X + b_{2}MO + b_{3}X*MO + e\]
\(b_{3}\)는 반드시 유의해야 한다.
Chapter 2. 다중공선성 진단
1. 진단도구
산점도_상관계수
다중공선성을 진단하는 가장 기본적인 출발점은 산점도 행렬과 상관계수 행렬이다. 회귀분석을 시작할 때, 먼저 산점도 행렬을 통해 종속변수와 각 설명변수의 관계를 시각적으로 살펴볼 수 있으며, 동시에 설명변수들 사이의 관계도 확인할 수 있다.
상관계수 행렬은 보다 정량적으로 설명변수들 간의 상관관계를 파악하게 해준다. 이를 통해 종속변수와 밀접한 관련이 있는 설명변수를 미리 선별할 수 있을 뿐만 아니라, 설명변수들 사이에 높은 상관이 존재한다면 다중공선성이 발생할 가능성을 사전에 진단할 수 있다.
이 방법은 직관적이고 계산이 간단하다는 장점이 있지만, 몇 가지 한계가 있다. 무엇보다 상관계수 행렬은 설명변수들 간의 쌍체(pairwise) 관계만 보여줄 뿐, 여러 변수들이 함께 작용하는 경우의 다중공선성을 직접 검정하지는 못한다. 또한 단순히 상관계수가 높다고 해서 반드시 심각한 다중공선성이 발생한다고 단정할 수 없고, 반대로 상관계수가 낮더라도 다중공선성이 존재할 수 있다.
따라서 산점도와 상관계수는 다중공선성을 ”예상하고 탐색하는 도구”일 뿐, 유의성 검정을 제공하지는 못한다는 점을 명확히 이해할 필요가 있다..
분산팽창지수 Variance Inflation Index \(VIF_{k} = \frac{1}{1 - R_{k}^{2}}\)
특정 예측변수를 목표변수로 하고 나머지 예측변수를 설명변수로 하여 회귀분석 한 후 결정계수를 구한다. 결정계수 \(R_{k}^{2}\) 값이 크다는 것은 \(X_{k}\)가 다른 예측변수들에 의해 충분히 설명되고 있다는 것이고 이는 바로 다중공선성 문제가 발생할 수 있다는 증거이다. 만약 결정계수 \(R^{2} = 0.9\)이면 분산팽창지수 \(VIF = 10\)이다.
다수의 예측변수들에 의해 설명되는 정도를 나타내지만 상관계수와 같이 두 개의(쌍체) 예측변수에 의한 진단에는 적절하지 못하다. VIF 진단 기준값은 다음과 같이 상이하다.
10 이상(심각한 수준): (Hair, J. F. Jr., Anderson, R. E., Tatham, R. L. & Black, W. C. (1995). Multivariate Data Analysis (3rd ed). New York: Macmillan.)
5이상(문제로 간즈): Ringle, Christian M., Wende, Sven, & Becker, Jan-Michael. (2015).
빅데이터에서는 보수적 기준으로 2.5를 사용한다.
상태지수 Condition Index \(CI = \sqrt{\frac{\lambda_{max}}{\lambda_{k}}}\)
예측변수의 공분산(상관계수)행렬을 이용하여 고유값 eigen value(\(\lambda_{k}\)) 를 구한다. 이에 대응하는 Norm 1인 고유벡터가 주성분 부하 loading 이다. 고유값은 원변수(설명변수)의 선 형결합에 의해 만들어진 주성분 변수의 원변수 변동에 대한 설명력이다. 그러므로 고유값가 크다는 것(상태지수 값이 큰 값) 주성분의 원 변수 변동에 설명력이 크다는 것을 의미한다.
고유벡터 내의 부하크기가 상대적으로 큰 변수들 간에는 상관관계가 높다는 것을 의미한다. 상태지수가 10이상(일반적으로 30이상)인 부하벡터에서 부하계수가 상대적으로 큰 변수들에 의해 다중공선성 문제가 발생한다고 진단할 수 있다.
권장 진단 방법
다중공선성을 진단할 때는 우선 분산팽창지수(VIF)를 활용하는 것이 일반적이다. 실무적으로는 VIF \geq 3을 기준으로 주의가 필요하다고 본다. 이때 단순히 모든 변수를 대상으로 일괄 판단하기보다는, 최종적으로 유의하다고 확인된 설명변수를 중심으로 검토하는 것이 바람직하다.
특히 최종 모형에서 추정된 회귀계수의 부호와, 해당 설명변수와 종속변수 간의 피어슨 상관계수 부호를 비교하는 것이 중요하다. 두 부호가 동일하다면, 비록 다중공선성이 존재한다고 하더라도 모형의 해석에 심각한 왜곡을 주지 않으므로 굳이 다중공선성을 해결할 필요가 없다.
| 구분 | 반드시 해결해야 하는 경우 | 해결하지 않아도 되는 경우 |
| 연구 목적 | 각 설명변수의 개별 효과 해석이 중요할 때 (정책·이론적 함의) | 예측력 확보가 주목적일 때 |
| 통계 지표 | VIF 값이 매우 큼 (예: 10 이상) / Condition Index ≥ 30 이상 | VIF 값이 다소 높더라도 (3~5 수준) |
| 회귀계수 | 추정된 회귀계수의 부호가 종속변수와 설명변수 간 피어슨 상관계수 부호와 불일치할 때 | 회귀계수 부호와 피어슨 상관계수 부호가 동일할 때 |
| 모형 안정성 | 표본을 바꿀 때 회귀계수 추정치가 크게 요동할 때 | 표본 변화에도 회귀계수가 크게 변하지 않을 때 |
# ============================================== # Boston Housing: Multicollinearity Diagnostics (All predictors - “ZN”제외 + Correlation) # ============================================== import numpy as np import pandas as pd import statsmodels.api as sm from sklearn.datasets import fetch_openml from statsmodels.stats.outliers_influence import variance_inflation_factor # ------------------------------------------------ |
전체 예측변수 목록: ['CRIM', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
[1] 상관계수 행렬 (medv 포함)
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX \
CRIM 1.000 -0.200 0.407 -0.056 0.421 -0.219 0.353 -0.380 0.626 0.583
ZN -0.200 1.000 -0.534 -0.043 -0.517 0.312 -0.570 0.664 -0.312 -0.315
INDUS 0.407 -0.534 1.000 0.063 0.764 -0.392 0.645 -0.708 0.595 0.721
CHAS -0.056 -0.043 0.063 1.000 0.091 0.091 0.087 -0.099 -0.007 -0.036
NOX 0.421 -0.517 0.764 0.091 1.000 -0.302 0.731 -0.769 0.611 0.668
RM -0.219 0.312 -0.392 0.091 -0.302 1.000 -0.240 0.205 -0.210 -0.292
AGE 0.353 -0.570 0.645 0.087 0.731 -0.240 1.000 -0.748 0.456 0.506
DIS -0.380 0.664 -0.708 -0.099 -0.769 0.205 -0.748 1.000 -0.495 -0.534
RAD 0.626 -0.312 0.595 -0.007 0.611 -0.210 0.456 -0.495 1.000 0.910
TAX 0.583 -0.315 0.721 -0.036 0.668 -0.292 0.506 -0.534 0.910 1.000
PTRATIO 0.290 -0.392 0.383 -0.122 0.189 -0.356 0.262 -0.232 0.465 0.461
B -0.385 0.176 -0.357 0.049 -0.380 0.128 -0.274 0.292 -0.444 -0.442
LSTAT 0.456 -0.413 0.604 -0.054 0.591 -0.614 0.602 -0.497 0.489 0.544
MEDV -0.388 0.360 -0.484 0.175 -0.427 0.695 -0.377 0.250 -0.382 -0.469
PTRATIO B LSTAT MEDV
CRIM 0.290 -0.385 0.456 -0.388
ZN -0.392 0.176 -0.413 0.360
INDUS 0.383 -0.357 0.604 -0.484
CHAS -0.122 0.049 -0.054 0.175
NOX 0.189 -0.380 0.591 -0.427
RM -0.356 0.128 -0.614 0.695
AGE 0.262 -0.274 0.602 -0.377
DIS -0.232 0.292 -0.497 0.250
RAD 0.465 -0.444 0.489 -0.382
TAX 0.461 -0.442 0.544 -0.469
PTRATIO 1.000 -0.177 0.374 -0.508
B -0.177 1.000 -0.366 0.333
LSTAT 0.374 -0.366 1.000 -0.738
MEDV -0.508 0.333 -0.738 1.000
[2] VIF (모든 변수)
variable VIF
8 TAX 8.560
7 RAD 7.401
3 NOX 4.388
1 INDUS 3.946
6 DIS 3.314
5 AGE 3.056
11 LSTAT 2.933
4 RM 1.887
0 CRIM 1.779
9 PTRATIO 1.625
10 B 1.348
2 CHAS 1.074
[3] Condition Index
eigenvalue condition_index
11 5.769 1.000
10 1.367 2.054
9 1.143 2.246
8 0.855 2.598
7 0.772 2.734
6 0.602 3.094
5 0.490 3.432
4 0.330 4.179
3 0.239 4.915
2 0.197 5.408
1 0.170 5.827
0 0.066 9.362
[3-1] Variance-Decomposition Proportions
eig1 eig2 eig3 eig4 eig5 eig6 eig7 eig8 eig9 eig10 \
CRIM 0.002 0.006 0.018 0.013 0.099 0.206 0.407 0.031 0.002 0.109
INDUS 0.064 0.024 0.038 0.468 0.136 0.085 0.016 0.013 0.000 0.013
CHAS 0.001 0.000 0.000 0.000 0.000 0.004 0.001 0.117 0.568 0.000
NOX 0.002 0.675 0.007 0.029 0.001 0.049 0.001 0.001 0.030 0.002
RM 0.001 0.021 0.038 0.156 0.060 0.054 0.016 0.121 0.016 0.374
AGE 0.001 0.063 0.321 0.018 0.147 0.161 0.003 0.026 0.034 0.033
DIS 0.006 0.080 0.317 0.091 0.164 0.033 0.002 0.045 0.034 0.007
RAD 0.415 0.014 0.015 0.082 0.076 0.068 0.011 0.016 0.038 0.134
TAX 0.505 0.051 0.003 0.000 0.032 0.159 0.003 0.018 0.019 0.067
PTRATIO 0.003 0.061 0.000 0.000 0.010 0.146 0.191 0.154 0.199 0.008
B 0.000 0.002 0.003 0.004 0.009 0.010 0.338 0.381 0.056 0.139
LSTAT 0.000 0.004 0.240 0.138 0.265 0.024 0.010 0.079 0.004 0.115
eig11 eig12
CRIM 0.035 0.072
INDUS 0.015 0.127
CHAS 0.309 0.000
NOX 0.079 0.124
RM 0.107 0.037
AGE 0.092 0.100
DIS 0.120 0.103
RAD 0.017 0.115
TAX 0.013 0.129
PTRATIO 0.186 0.043
B 0.011 0.047
LSTAT 0.016 0.103
[4] 전체 회귀 결과 요약
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.735
Model: OLS Adj. R-squared: 0.728
Method: Least Squares F-statistic: 113.7
Date: Thu, 04 Sep 2025 Prob (F-statistic): 1.68e-133
Time: 00:36:11 Log-Likelihood: -1504.6
No. Observations: 506 AIC: 3035.
Df Residuals: 493 BIC: 3090.
Df Model: 12
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 36.8633 5.156 7.150 0.000 26.733 46.993
CRIM -0.0983 0.033 -2.972 0.003 -0.163 -0.033
INDUS -0.0016 0.062 -0.025 0.980 -0.123 0.120
CHAS 2.7297 0.871 3.136 0.002 1.019 4.440
NOX -18.2289 3.857 -4.726 0.000 -25.808 -10.650
RM 4.0300 0.417 9.660 0.000 3.210 4.850
AGE -0.0047 0.013 -0.355 0.723 -0.031 0.021
DIS -1.2040 0.184 -6.526 0.000 -1.566 -0.841
RAD 0.2823 0.067 4.235 0.000 0.151 0.413
TAX -0.0095 0.004 -2.564 0.011 -0.017 -0.002
PTRATIO -1.0904 0.126 -8.679 0.000 -1.337 -0.844
B 0.0094 0.003 3.469 0.001 0.004 0.015
LSTAT -0.5156 0.051 -10.076 0.000 -0.616 -0.415
==============================================================================
Omnibus: 182.216 Durbin-Watson: 1.051
Prob(Omnibus): 0.000 Jarque-Bera (JB): 816.643
Skew: 1.554 Prob(JB): 4.66e-178
Kurtosis: 8.392 Cond. No. 1.51e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.51e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
[결론]
- 상관계수 행렬로 변수 간 높은 pairwise 관계 확인.
- VIF ≥ 5 (또는 10) → 다중공선성 문제 의심.
- Condition Index ≥ 30 → 다중공선성 가능, ≥ 100 → 심각.
회귀계수 부호와 단순 상관 부호가 다를 경우 해석 주의.
1. 상관계수 행렬
INDUS–NOX (0.764), RAD–TAX (0.910), NOX–DIS (-0.769) 같이 변수 간 높은 상관이 존재합니다.
LSTAT는 MEDV와 -0.738, RM은 MEDV와 0.695로 강한 상관 → 주택가격의 핵심 설명변수임을 확인.
따라서, 일부 예측변수는 서로 매우 비슷한 정보를 담고 있음(중복 설명력).
2. VIF
TAX(8.56), RAD(7.40) → 공선성 높은 변수 후보.
NOX(4.39), INDUS(3.95), DIS(3.31), AGE(3.06)도 다소 높은 값.
”RAD–TAX”가 대표적 다중공선성 원인 쌍임을 알 수 있음.
3. Condition Index
최대 Condition Index = 9.36, 기준선(30 이상)에는 미치지 않음.
즉, 심각한 다중공선성은 아님. 다만 분산분해비(Proportions)를 보면 특정 고유성분에서 RAD, TAX, NOX 등이 같이 큰 값을 가짐 → 이 변수들이 공선성에 기여.
OLS 결과의 condition number = 1.51e+04는 수치적으로 큰 편이라, 다중공선성 가능성을 경고. (표준화/스케일 차이의 영향도 일부 있음.)
4. OLS 결과
모형 설명력: 결정계수 73.5%로 모든 예측변수는 주택가격 변동의 73.5% 설명 → 상당히 높은 수준이다.
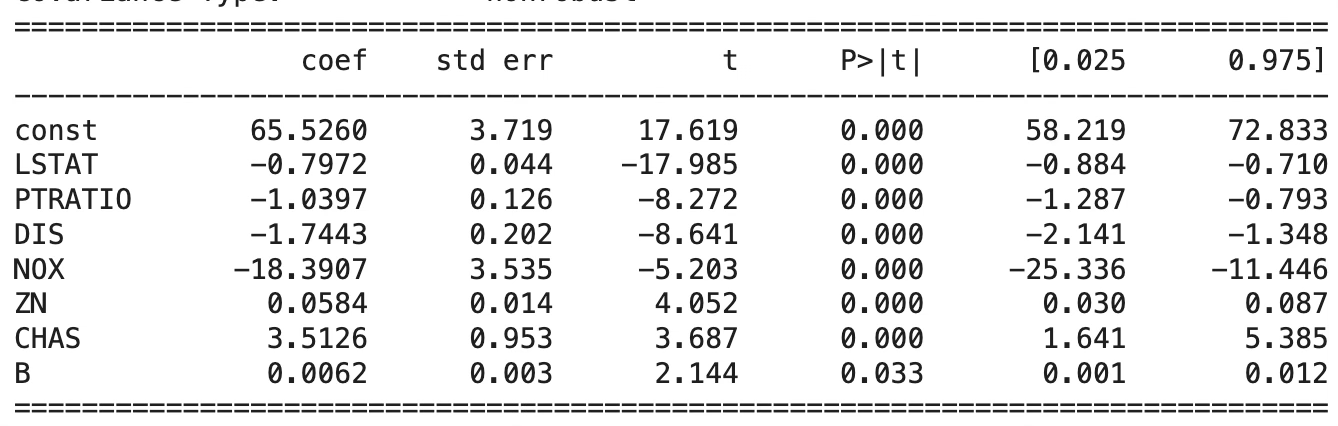
주요 유의 변수: RM(방 개수, 양수 효과), LSTAT(저소득층 비율, 음수 효과), PTRATIO(학생-교사 비율, 음수 효과), NOX(대기오염도, 음수 효과), DIS(도심 접근성, 음수 효과), RAD, TAX, B, CHAS.
비유의 변수: INDUS, AGE → 높은 상관은 있지만 독립적으로 설명력 없음. 이는 다른 변수들과 중복된 영향(공선성) 때문.
RAD 예측변수는 목표변수와 음의 상관관계가 있는데 회귀계수는 양이므로 RAD–TAX”가 대표적 다중공선성 원인 쌍임으로 보여주므로 TAX보다 목표변수와 상관관계가 낮은 RAD 변수는 제외하는 것이 적절하다.
5. 종합 결론
다중공선성 신호: RAD–TAX, INDUS–NOX–DIS–AGE. → 이들 변수는 서로 강하게 연결되어 있어, 개별 해석은 조심해야 함.
해석 안정성: 주요 변수 RM(+), LSTAT(-), PTRATIO(-)는 상관계수 부호와 회귀계수 부호가 일치 → 해석 신뢰 가능.
RAD 변수를 제외하고, 예측변수의 유의성을 검증한 후 회귀진단을 실시하면 된다.
예측 vs 해석: 전체 모형은 예측에는 강력하지만, 각 설명변수의 순수 효과 해석은 일부 왜곡 가능성이 있음. 정책적 함의를 뽑아내려면 변수 선택/차원축소(예: Ridge, PCA 회귀)가 바람직.
최종 회귀모형
RM은 변수선택에서 제외
RAD는 다중공선성 문제 발생으로 제외
# ============================================== # 최종 회귀모형 선택 # ============================================== import pandas as pd import numpy as np import statsmodels.api as sm from sklearn.datasets import fetch_openml # --- 0) 데이터 로드 --- boston = fetch_openml(name="boston", version=1, as_frame=True) df = boston.frame.copy() # 종속변수 / 설명변수 y = pd.to_numeric(df["MEDV"], errors="coerce") X = df.drop(columns=["MEDV", "RM", "RAD","DIS","AGE"]).copy() |
단계선택 방법: 결정계수 67.1%
DIS: 목표변수와 상관계수 부호와 회귀계수 부호 상이 -> 경고문에 다중 공선성 문제 발생 출력
다시 단계선택 방법을 적용한 결과 AGE 변수도 동일한 문제 발셍 -> 경고문에 다중 공선성 문제 발생 출력
Chapter 3. 다중공선성 해결방안
구조적 다중공선성 문제 해결 - 예측변수 centering (중심화) - 다항식 모형(예측변수의 제곱항, 세제곱항)에 적합
표준화는 데이터의 평균과 표준편차를 활용하여 단위를 없앤 개념임 : \(z_{i} = \frac{x_{i} - {\overline{x}}_{i}}{s(x_{i})}\)
중심화는 데이터의 평균을 0으로 이동한 개념임, 산포는 동일하게 유지됨 : \(c_{i} = x_{i} - {\overline{x}}_{i}\)
문제변수 제거
다중공선성 문제가 되는 설명변수를 제외한다.
여러개가 존재하는 경우 목표변수와 상관관계가 낮은 예측변수를 제외한다.
1. 주성분 분석
주성분분석(PCA)은 여러 개의 상관된 변수들을, 서로 상관이 없는 새로운 변수들(주성분, principal components)로 변환하는 차원 축소 방법이다. 각 주성분은 원래 변수들의 선형결합으로 만들어지며, 첫 번째 주성분은 데이터 변동성을 가장 크게 설명하고, 두 번째 주성분은 그 다음으로 큰 변동성을 설명하되 첫 번째 주성분과 직교(orthogonal)하도록 구성된다.
즉, PCA의 목적은 복잡하게 얽힌 변수들의 중복된 정보를 제거하고, 데이터의 주요한 구조를 단순화하는 데 있다. 주성분분석은 단순히 데이터 요약 방법이 아니라, 다중공선성 문제를 해결할 수 있는 강력한 도구이다. 원래 변수들 간의 상관관계를 제거하고 새로운 직교 좌표축을 제공하기 때문에, 예측력을 유지하면서 회귀계수의 안정성을 높여준다. 다만, 주성분의 해석이 직관적이지 않다는 점을 감안하여, 예측이 목적일 때 특히 효과적이고, 해석이 목적일 때는 신중하게 적용해야 한다.
다중공선성은 예측변수들 간의 높은 상관관계에서 발생한다. 여러 변수가 서로 비슷한 정보를 담고 있기 때문에, 회귀분석에서 회귀계수가 불안정해지고 표준오차가 커지는 문제가 생긴다.
PCA를 적용하면 원래 상관관계가 높던 변수들을 서로 독립적인 주성분으로 변환할 수 있다. 이렇게 하면 회귀모형에 투입되는 설명변수들 사이의 공선성이 사라지고, 안정된 계수 추정이 가능해진다.
해결 방안으로서 PCA의 활용
PCA를 통해 얻은 주성분들을 새로운 설명변수로 사용하여 회귀분석을 수행한다.
주성분들은 서로 독립적이므로 다중공선성 문제가 해소된다.
다만, 주성분은 원래 변수의 해석이 쉽지 않다는 단점이 있다.
차원 축소 효과
설명력이 낮은 주성분을 제외하고 상위 몇 개의 주성분만 사용하면, 변동성을 유지하면서 불필요한 잡음과 다중공선성을 동시에 줄일 수 있다.
예를 들어, 원래 10개 변수로 구성된 데이터라도 상위 34개의 주성분으로 전체 변동성의 8090%를 설명할 수 있다면, 훨씬 단순하고 안정적인 모형을 얻을 수 있다.
# ============================================== # PCA (주성분분석) + Principal Component Regression # ============================================== import numpy as np import pandas as pd from sklearn.datasets import fetch_openml from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA import statsmodels.api as sm |
예측변수 목록: ['CRIM', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
[1] 각 주성분 설명 분산 비율
[0.481 0.114 0.095 0.071 0.064 0.05 0.041 0.028 0.02 0.016 0.014 0.005]
[2] 누적 설명력
[0.481 0.595 0.69 0.761 0.825 0.876 0.916 0.944 0.964 0.98 0.995 1. ]
[3] 주성분 부하량 (원 변수 → 주성분 기여도)
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 \
CRIM 0.268 -0.186 0.330 0.046 -0.177 0.638 0.454 -0.315 0.114 0.135
INDUS 0.356 0.124 -0.114 0.009 0.112 -0.128 -0.292 -0.369 0.684 0.196
CHAS 0.003 0.555 0.010 0.753 -0.342 -0.029 0.066 0.020 -0.003 -0.015
NOX 0.352 0.280 -0.045 -0.173 0.026 0.032 -0.221 -0.033 -0.171 0.083
RM -0.193 0.328 0.611 -0.127 0.348 -0.126 0.232 0.244 0.395 -0.195
AGE 0.317 0.304 -0.181 -0.185 0.160 -0.054 0.402 0.384 -0.135 0.566
DIS -0.321 -0.346 0.082 0.183 -0.212 0.047 -0.181 0.405 0.301 0.563
RAD 0.339 -0.131 0.366 0.194 0.125 0.105 -0.261 0.276 -0.287 -0.122
TAX 0.359 -0.115 0.258 0.138 0.133 0.054 -0.399 0.180 -0.012 0.053
PTRATIO 0.207 -0.431 -0.091 0.446 0.393 -0.437 0.382 -0.098 -0.008 -0.015
B -0.217 0.105 -0.373 0.237 0.617 0.582 -0.102 0.093 0.065 -0.054
LSTAT 0.321 -0.127 -0.339 -0.062 -0.281 0.102 0.155 0.515 0.371 -0.490
PC11 PC12
CRIM 0.075 0.041
INDUS -0.154 -0.254
CHAS -0.002 0.037
NOX 0.822 0.048
RM 0.144 0.033
AGE -0.251 -0.031
DIS 0.282 -0.075
RAD -0.116 -0.644
TAX -0.227 0.711
PTRATIO 0.247 0.050
B 0.040 -0.006
LSTAT 0.067 0.018
[4] 주성분 점수 DataFrame (앞부분)
PC1 PC2 PC3 PC4 PC5 PC6 PC7 \
0 -2.100508 0.794845 0.098831 -0.978169 -0.095970 0.507272 -0.023877
1 -1.649298 0.094635 -0.483831 -0.397519 0.141078 -0.028798 0.605383
2 -2.280518 0.345673 0.555412 -0.384408 0.592043 -0.231237 0.497210
3 -2.826744 -0.361504 0.637358 0.061903 0.436344 -0.235396 0.502932
4 -2.669692 -0.242109 0.591630 -0.035176 0.478284 -0.226862 0.723477
PC8 PC9 PC10 PC11 PC12
0 -0.043068 -0.750781 0.223956 0.029284 0.362596
1 0.183476 -0.022345 0.529996 -0.219936 -0.128753
2 -0.166574 0.223905 0.313149 0.045882 -0.085665
3 -0.070508 -0.213217 0.249970 0.429724 -0.080312
4 0.269469 -0.043381 0.212839 0.408998 -0.076439
[5] PCR 결과 (상위 5개 주성분 사용)
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.699
Model: OLS Adj. R-squared: 0.696
Method: Least Squares F-statistic: 232.1
Date: Thu, 04 Sep 2025 Prob (F-statistic): 8.56e-128
Time: 01:21:30 Log-Likelihood: -1536.6
No. Observations: 506 AIC: 3085.
Df Residuals: 500 BIC: 3111.
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 22.5328 0.225 99.931 0.000 22.090 22.976
PC1 -2.3446 0.094 -24.974 0.000 -2.529 -2.160
PC2 3.1494 0.193 16.329 0.000 2.770 3.528
PC3 2.9981 0.211 14.218 0.000 2.584 3.412
PC4 -0.3160 0.244 -1.296 0.196 -0.795 0.163
PC5 2.0885 0.257 8.139 0.000 1.584 2.593
==============================================================================
Omnibus: 235.315 Durbin-Watson: 0.967
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1735.425
Skew: 1.882 Prob(JB): 0.00
Kurtosis: 11.255 Cond. No. 2.73
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
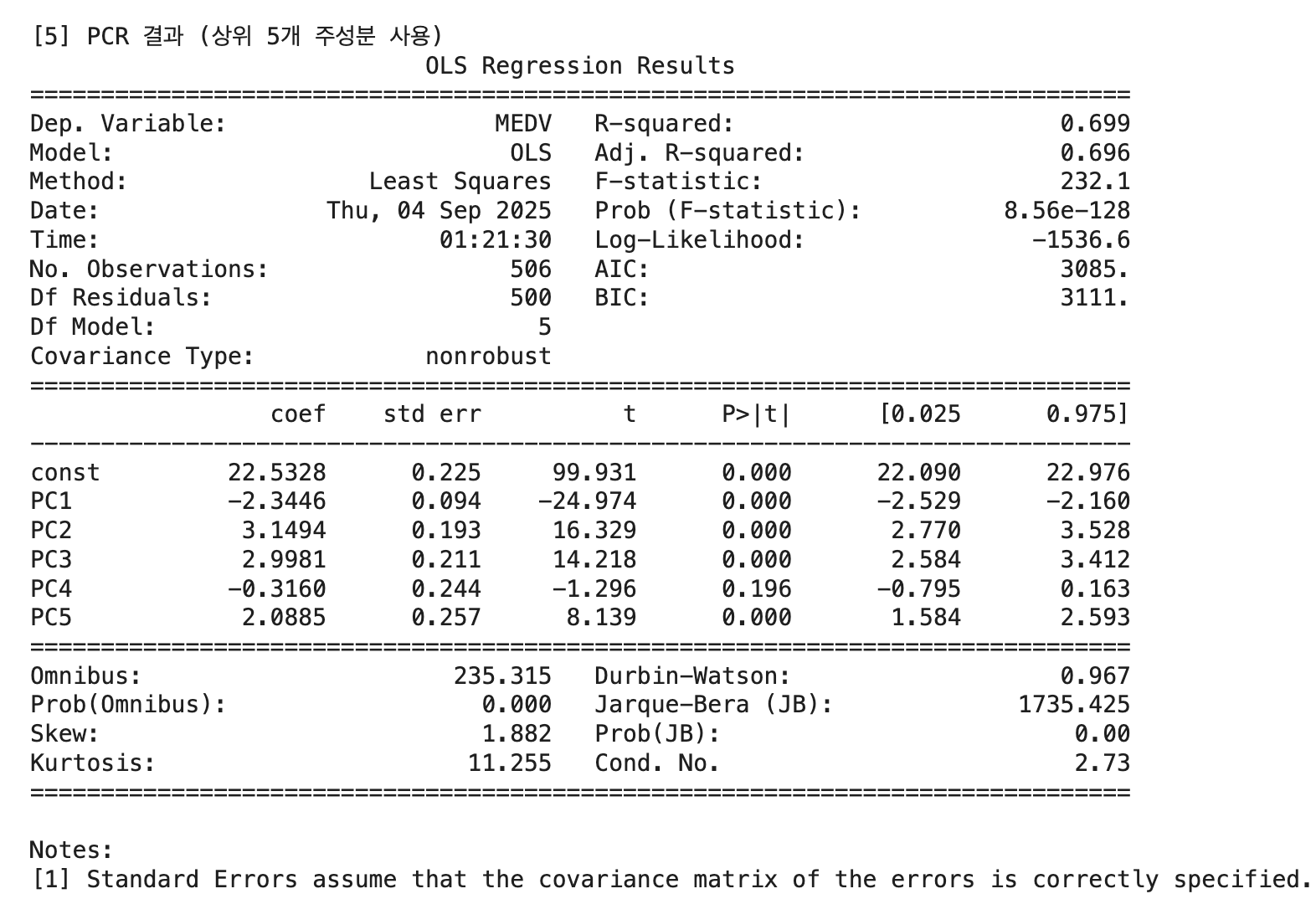
1. PC1 (분산 비율 48.1%)
• CRIM(+), INDUS(+), NOX(+), AGE(+), TAX(+), LSTAT(+) vs RM(-), DIS(-), B(-)
• 해석: 도시집중·노후·환경악화 축
→ 범죄율, 공업비율, 공해, 노후주택, 세금, 저소득층 비율이 높고, 방 개수·쾌적성은 낮은 방향
이름 제안: ”도시 낙후·환경 악화 요인”
2. PC2 (11.4%)
• CHAS(+), RM(+), AGE(+), NOX(+), vs PTRATIO(-), DIS(-)
• 해석: 강변·주거환경·교육조건 축
→ 찰스강 인접, 방 개수와 노후도, 환경이 관련되며, 학급당 학생수(PTRATIO)와 도심거리(DIS)는 반대
이름 제안: ”강변 주거환경·교육 조건 요인”
⸻
3. PC3 (9.5%)
• RM(+), RAD(+), TAX(+), CRIM(+), vs B(-), LSTAT(-)
• 해석: 주거규모·교통·재정 축
→ 방이 많고 교통 접근성(RAD, TAX)과 범죄율이 높을수록, 흑인비율(B)과 저소득층 비율(LSTAT)은 반대
이름 제안: ”주거규모·교통 재정 요인”
⸻
4. PC4 (7.1%)
• CHAS(+), PTRATIO(+), B(+), INDUS(+), 일부 환경 변수와 약한 관련
• 해석: 특수 입지·교육 인프라 축
→ 찰스강 인접, 교육 환경, 일부 산업 비율 등이 섞여 있는 보조 요인
이름 제안: ”입지·교육 보조 요인”
⸻
5. PC5 (6.4%)
• B(+), RM(+), PTRATIO(+), 일부 LSTAT(-)
• 해석: 주택 품질·사회구성 축
→ 흑인비율, 방 개수, 학급당 학생 수와 연관 → 주거 품질과 사회적 요인이 혼합
이름 제안: ”주택 품질·사회구성 요인”
2. 능형 회귀분석 Ridge Regression
다중공선성은 회귀계수의 추정오차를 증가시키므로 불편성(OLS는 불편 추정량이다)을 포기하는 대신 MSE(Mean Square of Error 평균오차자승합)를 최소화 하는 편기(biased) 추정량을 구하는 추정 방법을 사용함으로써 다중공성선 문제를 해결하는데 이를 능형 회귀분석((Ridge Regression)이라 한다.
편기 추정량 \(\widehat{{\underset{¯}{b}}_{*}} = (X'X + \lambda I)X'\underset{¯}{y}\)의 \(MSE(\widehat{{\underset{¯}{b}}_{*}}) = E(\widehat{{\underset{¯}{b}}_{*}} - \underset{¯}{b})^{2}\)를 최소화 하는 \(0 < \lambda\)를 구하면 이를 능형 추정량이라 한다. \(c = 0\)이면 OLS 추정값이다.
상수 \(c\)와 VIF 산점도를 이용하여 각 예측변수의 추정 회귀계수 값이 안정화 되는 \(c\)값을 최적값으로 설정한다. 다소 주관적이다.
Ridge 회귀는회귀계수 해석”보다는 ”예측 안정성 향상에 초점을 두므로 OLS처럼 ”이 변수가 유의하다/아니다”를 말하기 위해 쓰는 기법은 아니다.
# ============================================== # 능형 Regression # ============================================== import numpy as np import pandas as pd from sklearn.datasets import fetch_openml from sklearn.preprocessing import StandardScaler from sklearn.linear_model import RidgeCV from sklearn.pipeline import Pipeline from sklearn.metrics import mean_squared_error from sklearn.model_selection import KFold # 데이터 boston = fetch_openml(name="boston", version=1, as_frame=True) df = boston.frame.dropna().reset_index(drop=True) y = df["MEDV"] X = df.drop(columns=["MEDV","ZN"]) # 후보 λ (alpha)들 alphas = np.logspace(-3, 3, 100) # 파이프라인: 표준화 + RidgeCV(K-fold) pipe = Pipeline([ ("scaler", StandardScaler()), ("ridge", RidgeCV(alphas=alphas, cv=KFold(n_splits=10, shuffle=True, random_state=42), scoring="neg_mean_squared_error")) ]) pipe.fit(X, y) best_alpha = pipe.named_steps["ridge"].alpha_ coefs = pipe.named_steps["ridge"].coef_ print("최적 λ(alpha):", best_alpha) print(“추정 회귀계수:", pd.Series(coefs, index=X.columns).sort_values(key=abs, ascending=False)) |
최적 λ(alpha): 4.9770235643321135
추정회귀 계수(상위 5개): LSTAT -3.625057
RM 2.852304
DIS -2.451308
PTRATIO -2.298852
RAD 2.188506
NOX -1.981206
TAX -1.381737
B 0.855040
CRIM -0.815508
CHAS 0.704650
AGE -0.152481
INDUS -0.094937