다변량분석 2. 주성분분석

Chapter 1. 차원축소 개념

1. 특성 추출이란

대용량 데이터 \(X_{n \times p}\)에서 행 n은 개체, 열 p는 변수를 나타낸다. 개체의 특성을 시각화하거나 분석하기 위해서는 변수가 매우 많을 경우 차원을 축소할 필요가 있다. 이를 feature extraction(특성 추출)이라고 한다. 특성 추출은 원 데이터의 구조적 관계를 활용하여 새로운 변수를 생성하거나, 고차원의 공간을 저차원의 새로운 공간으로 사상하는 방식으로 이루어진다.

예를 들어 변수 간 상관계수를 유사성 척도로 활용하여 변수 구조를 탐색하기도 한다. 대표적인 방법으로는 주성분분석(PCA), 특이값 분해(SVD)에 기반한 차원축소 기법이 있으며, 두 변수 집합 간의 상관성을 극대화하는 정준상관분석(CCA)도 새로운 특성을 생성한다는 점에서 넓은 의미의 특성 추출 과정으로 이해할 수 있다. 이러한 방법들은 협의의 차원 축소에 속한다.

특성 선택은 변수에 중요도나 우선순위를 부여하여 목표 변수에 영향을 주는 주요 변수의 부분집합을 선택하거나, 불필요한 변수를 제거하여 변수의 차원(개수)을 줄이는 과정이다. 예를 들어, 의사결정나무 모형에서는 트리 상단에 위치하는 변수가 중요도가 높으며, 이를 바탕으로 변수별 중요도를 평가할 수 있다. 회귀모형에서는 단계적 선택법과 같은 유의 변수 선택 알고리즘을 활용하여 변수 선택이 가능하다.

특성 선택 기법에는 상관분석과 같은 통계적 방법, 라쏘 회귀·재귀적 특성 제거법·트리 기반 모형, 그리고 판별분석이나 로지스틱 회귀기반 방법 등이 있다.

2. 차원축소와 주성분분석

차원축소는 말 그대로 데이터를 요약하는 과정이다. 변수가 지나치게 많을 때, 모든 변수를 그대로 두고 분석하는 것은 계산량도 커지고 해석도 어렵다. 그래서 정보 손실을 최소화하면서도 적은 수의 새로운 변수로 데이터를 표현하는 방법이 필요하다. 이를 통해 데이터는 단순해지면서도 본질적인 구조와 패턴은 유지할 수 있다. 차원축소의 목적은 크게 두 가지로 볼 수 있는데, 하나는 데이터 시각화를 가능하게 하는 것이고, 다른 하나는 분석 효율성을 높이는 것이다. 시각화는 고차원 데이터를 2차원이나 3차원으로 줄여 그림으로 표현할 수 있게 해 주며, 효율성 측면에서는 계산 속도 향상, 불필요한 잡음 제거, 다중공선성 문제 완화, 저장·전송의 압축 효과 등을 제공한다.

주성분분석(PCA)은 이러한 차원축소 방법 가운데 가장 널리 쓰이는 전형적인 기법이다. PCA는 데이터가 분산을 가장 크게 보이는 방향을 찾아 새로운 좌표축을 세우고, 그 축을 따라 데이터를 재배치한다. 첫 번째 주성분은 데이터가 가장 넓게 퍼진 방향이고, 두 번째 주성분은 첫 번째와 직교하면서 그다음으로 넓게 퍼진 방향이다. 이렇게 이어지는 주성분들은 서로 독립적이면서도 데이터의 구조를 가장 잘 설명하는 순서대로 배열된다. 따라서 처음 몇 개의 주성분만으로도 원래 데이터의 대부분의 변동성을 설명할 수 있다.

주성분분석을 통해 얻어지는 결과는 크게 두 가지이다. 하나는 각 개체가 새로운 좌표축에서 어디에 위치하는지를 보여 주는 점수이고, 다른 하나는 새로운 좌표축이 원래 변수들의 어떤 조합으로 만들어졌는지를 알려 주는 적재치이다. 점수는 개체들 사이의 유사성과 차이를 시각적으로 드러내는 데 유용하며, 적재치는 어떤 변수가 서로 묶여 함께 움직이는지를 해석할 수 있게 해 준다.

결국 차원축소는 데이터의 복잡성을 줄이는 큰 틀의 개념이고, 주성분분석은 그 안에서 가장 대표적이고 직관적인 방법이라고 할 수 있다. 주성분분석은 데이터를 요약하면서도 시각화를 쉽게 하고, 노이즈를 줄이며, 다중공선성과 같은 문제를 완화하는 데 효과적이다. 따라서 차원축소와 주성분분석은 포괄적 개념과 구체적 방법의 관계로 이해할 수 있다.

3. 차원축소 방법론

주성분분석은 차원축소 기법들 가운데 가장 기본적이고 널리 쓰이는 방법이지만, 다른 기법들과의 관계를 이해하면 언제 어떤 방법을 선택해야 하는지 분명해진다.

먼저 특이값분해(SVD)는 구현 관점에서 PCA와 사실상 같은 몸이라고 볼 수 있다. 데이터를 평균 중심화한 뒤 SVD를 적용하면 곧바로 PCA의 주성분을 얻을 수 있다. 실제로 대용량 데이터에서는 SVD 기반의 계산 방식이 주로 사용되며, 속도와 메모리 문제를 해결하기 위해 랜덤화된 SVD나 점진적 SVD와 같은 변형 기법들이 활용된다.

요인분석(FA)은 겉보기에는 PCA와 비슷해 보이지만, 목적은 다르다. 요인분석은 공통된 잠재 요인으로 변수들의 공분산 구조를 설명하려는 모형 기반 접근이다. 반면 PCA는 단순히 분산을 최대화하는 새로운 축을 찾는 기하학적 요약 방식이다. 그래서 요인분석은 해석 가능성을 중시할 때, PCA는 데이터 요약과 압축이 필요할 때 주로 쓰인다.

독립성분분석(ICA)와 비음수행렬분해(NMF)는 데이터 구조를 바라보는 또 다른 시각을 제공한다. ICA는 변수들 간의 독립성을 극대화하려 하고, NMF는 변수들을 음수가 아닌 조합으로만 표현한다는 제약을 둔다. 두 방법 모두 PCA와 달리 분산 대신 다른 기준을 사용해 차원을 축소하며, 데이터의 성질과 해석 목적에 따라 선택된다.

부분최소제곱회귀(PLS)나 선형판별분석(LDA)은 PCA와 달리 감독학습 기반의 차원축소 기법이다. 이들은 목표변수(y)의 정보를 활용하여 새로운 축을 찾기 때문에, 예측 성능을 높이고자 할 때 주로 적용된다. PCA가 목표변수를 고려하지 않는 비감독적 방법이라는 점과 대비된다.

마지막으로 커널 PCA는 비선형 구조를 포착하기 위한 확장판이다. PCA가 선형 변환만으로는 잡아내기 힘든 곡선적·비선형적 패턴을, 고차원 공간에서의 변환을 통해 드러내는 방식이다. 따라서 복잡한 데이터 구조를 다루는 데 유리하다.

정리하면, PCA는 차원축소의 출발점이자 기본형이고, 다른 기법들은 목적과 데이터의 특성에 따라 PCA의 한계를 보완하거나 대체하는 방식으로 발전해왔다고 볼 수 있다.

Chapter 2. 주성분분석

1. 주성분분석 개념

(1) 공간적 개념

이차원 공간 정보(아래 그림)를 1차원(직선)으로 표시한다면 어디에서 봐야 희생되는 정보(나무의 위치와 거리)가 최소일까? 만약 (1)에서 본다면 1번 나무에 가려 2번 나무는 직선 상에 나타나지 않아 나무가 2개 인 것처럼 보인다. (2)의 관점에서 본다면 역시 3번 나무로 인하여 2번 나무가 가려져 직선 상에 나타나지 않는다.

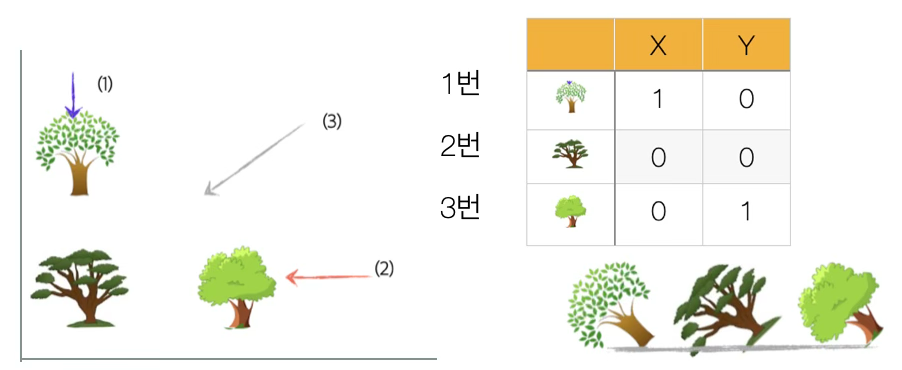
나무의 공간 정보를 최소화하는 관점은 (3)에서 보는 것이다. 그러나 이 역시 희생되는 정보가 있다. 2차원 공간에 있을 때 각 나무의 거리는 직선 상에서는 실제 거리 \(\sqrt{2}\)보다 가까워졌다. 이는 2차원 공간 정보를 1차원 직선으로 표현하여 잃은 정보가 존재한다는 것이다.

주성분분석은 이처럼 희생되는 정보를 최소화 하면서 데이터의 차원을 축약하는 방법이다. 다음은 주성분 분석을 활용하여 다차원 데이터를 2차원 공간에 축소하여 개체를 시각화 하고 개체를 군집화 하는 과정을 보여 준 것이다. 이처럼 주성분 분석은 최종 분석이 아니라 중간 단계 분석에 해당된다.

주성분분석(PCA)은 고차원 데이터 속에서 분산이 가장 큰 방향을 찾아 새로운 축을 설정하는 방법이다. 고차원 공간에 존재하는 데이터 점들은 서로 뒤섞여 있어 구조를 파악하기 어렵다. 그러나 주성분분석을 통해 데이터를 새로운 좌표축, 즉 주성분 축으로 투영하면 원래 보이지 않던 패턴이나 군집이 드러나게 된다.

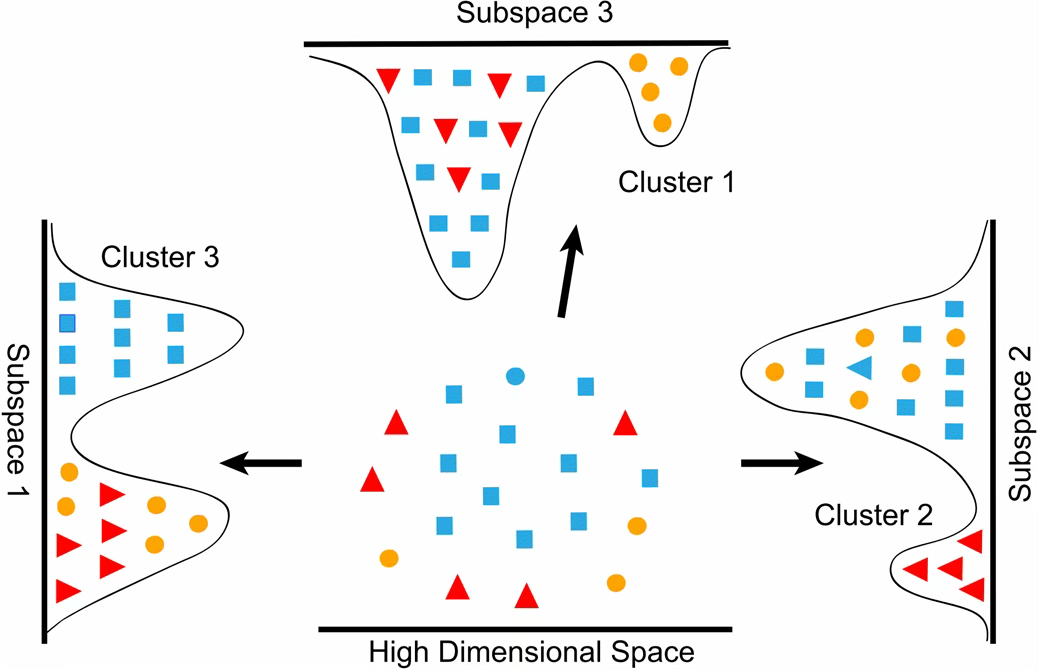
그림의 중앙에 있는 점은 원래의 고차원 공간을 나타낸 것이다. 이 공간에서는 점들이 무질서하게 흩어져 있어 클러스터를 구분하기가 쉽지 않다. 하지만 주성분축(Subspace)으로 투영하면 상황이 달라진다. Subspace 1로 데이터를 비추면 Cluster 3이, Subspace 2로 투영하면 Cluster 2가, Subspace 3에서는 Cluster 1이 명확하게 드러난다. 이는 주성분분석이 데이터의 분산이 큰 방향을 찾아내어 차원을 축소하면서 동시에 데이터의 내재된 구조를 보존한다는 것을 보여준다.

결국 주성분분석은 차원축소를 통해 데이터의 복잡성을 줄이면서도, 군집이나 패턴과 같은 중요한 구조적 특징을 드러내는 대표적인 방법이다.

(2) 활용사례

주성분분석은 많은 변수로 이루어진 데이터를 소수의 핵심 지표로 요약하는 방법이다. 온라인에서 옷을 구입하는 사례가 좋은 비유가 된다. 상의는 단순히 55사이즈, M사이즈와 같이 하나의 값으로 표현되며, 하의 역시 허리둘레 34인치와 같이 하나의 수치로 표시된다. 그러나 맞춤옷을 구입하려면 어깨 넓이, 어깨에서 손목까지의 길이, 허벅지 두께, 허리에서 무릎까지의 길이, 무릎에서 발꿈치까지의 길이 등 다양한 신체 치수를 측정해야 한다. 이 많은 정보가 결국 하나의 단위로 축약된 것이 바로 55사이즈나 34인치라는 값이다. 이러한 값은 다른 여러 치수 정보를 반영하는 일종의 골든 지표, 즉 주성분이라고 볼 수 있다. 따라서 많은 정보를 하나로 요약하는 과정에서 세부적인 차이가 사라지므로, 온라인에서 구매한 옷이 모든 사람의 체형에 꼭 맞지 않는 것이다. 이 때문에 Big & Tall 매장이나 디자이너 매장이 따로 존재한다.

이미지 데이터 역시 주성분분석의 활용을 이해하기 좋은 예다. 이미지 데이터는 기본적으로 가로, 세로, 색상 채널을 포함하는 3차원 공간 데이터이다. 그러나 통계 분석이나 기계학습에 활용하려면 이를 2차원 행렬 데이터로 축약해야 한다. 축약 과정을 사람이 직접 설계한다면 학습지도 기법, 즉 전통적 머신러닝에 해당한다. 반대로 컴퓨터가 스스로 중요한 특징을 찾아내는 경우는 비학습지도 기법, 즉 딥러닝에 해당한다. 이러한 학습 과정에서 널리 쓰이는 알고리즘으로는 서포트 벡터 머신(SVM), 아다부스트(AdaBoost) 등이 있다.

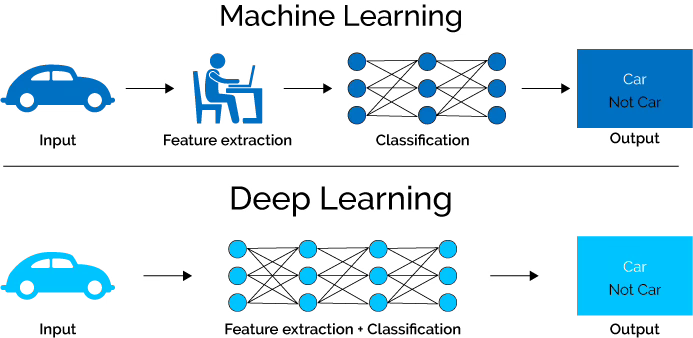
이미지나 음성, 텍스트와 같은 데이터는 본질적으로 고차원 공간에 존재한다. 예를 들어 자동차 사진은 수많은 픽셀 값으로 이루어져 있어 차원이 수천에서 수백만에 이른다. 이렇게 높은 차원의 데이터를 바로 다루기는 어렵기 때문에, 먼저 핵심 정보를 유지하면서 데이터의 차원을 축약하는 과정이 필요하다.

머신러닝은 차원축약과 특징 추출을 사람이 직접 설계하고 정의하는 방식이다. 분석자가 중요한 특징을 선택하거나 PCA와 같은 방법을 통해 차원을 줄인 후, 그 결과를 학습 알고리즘(SVM, AdaBoost 등)에 입력한다. 이때 분류기는 입력된 특징을 바탕으로 자동차인지 아닌지를 판별한다. 따라서 머신러닝은 사람이 특징을 만들어주고, 알고리즘은 그것을 이용해 학습하는 방식이다.

딥러닝은 이와 달리 사람이 직접 특징을 설계하지 않는다. 인공신경망이 여러 층을 거치면서 데이터를 단계적으로 변환하여 스스로 중요한 특징을 추출하고 차원을 축약한다. 즉, 원본 이미지가 그대로 신경망에 입력되면, 네트워크 내부에서 차원축약과 특징 추출이 동시에 이루어지고, 마지막 단계에서 자동차인지 아닌지의 판별이 자동으로 수행된다. 이는 기계가 스스로 특징을 학습하는 방식이다.

따라서 머신러닝과 딥러닝의 차이는 차원축약과 특징 추출이 사람의 설계에 의해 이루어지느냐, 기계가 스스로 학습하느냐에 있다. 그림은 이를 시각적으로 보여주며, ”Car vs Not Car”라는 단순한 예시를 통해 두 접근법의 차이를 직관적으로 설명한다.

2. 주성분 구하기

(1) 데이터 행렬, 변수벡터

데이터 행렬 (개체 행 n, 변수 열 p) : \(X_{n \times p} = \begin{pmatrix} x_{11} & x_{12} & ... & x_{1p} \\ x_{21} & x_{22} & ... & x_{2p} \\ & ... & & \\ x_{n1} & x_{n2} & ... & x_{np} \end{pmatrix}\)

변수벡터 : \({\underset{¯}{x}}_{1 \times p} = \left( \begin{array}{r} x_{1} \\ x_{2} \\ ... \\ x_{p} \end{array} \right)\), \(x_{i}\)는 i -번째 확률변수이며 \(\underset{¯}{x} \sim (\underset{¯}{\mu},\Sigma)\) 다변량 분포이다.

평균벡터: \({\underset{¯}{\mu}}_{1 \times p} = \left( \begin{array}{r} \mu_{1} \\ \mu_{2} \\ ... \\ \mu_{p} \end{array} \right)\), \(E(x_{i}) = \mu_{i}\)

공분산 행렬 \(\Sigma_{p \times p} = \begin{pmatrix} \sigma_{11} & \sigma_{12} & ... & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & ... & \sigma_{2p} \\ & ... & & \\ \sigma_{p1} & \sigma_{p2} & ... & \sigma_{pp} \end{pmatrix}\)

(2) 주성분 전처리

데이터에서 개체를 설명하는 변수의 구조는 변수들의 변동성과 공변동에 의해 요약된다. 이 구조를 수량화하는 대표적 도구가 공분산행렬이며, 변수의 단위와 규모 차이를 제거하여 비교 가능하게 만든 것이 상관행렬이다. 공분산행렬은 각 변수의 측정 단위와 규모(분산)를 그대로 반영하는 반면, 상관행렬은 변수를 평균 0, 분산 1로 표준화한 뒤의 상호 관련성을 반영한다.

따라서 변수의 단위가 같고 분산의 크기 차이가 의미 있는 정보라면 공분산행렬을 사용하는 것이 타당하다. 반대로 변수의 단위가 서로 다르거나, 분산의 규모 차이로 특정 변수가 결과를 지배할 우려가 있으면 상관행렬(= 표준화 후 공분산행렬)을 사용하는 것이 바람직하다. 상관행렬 기반 PCA는 곧 표준화 변수를 입력으로 한 공분산 기반 PCA와 동치이다. 한편, 두 경우 모두 중심화(평균 0)는 필수적이다.

확률변수(데이터) \(x_{i}\)의 평균은 \(\overline{x}\), 표준편차를 \(s(x)\)라 하자.

중심화 centering : \(c_{i} = x_{i} - \overline{x}\), 변수의 평균만 0으로 이동한다.

표준화 standardization : \(z_{i} = \frac{x_{i} - \overline{x}}{s(x)}\): 평균=0, 표준편차 1로 변환한다.

상황 중심화 필요 여부 표준화 필요 여부 사용 행렬
모든 변수가 같은 단위, 분산 차이 의미 있음 필요 불필요 공분산 행렬
모든 변수가 같은 단위, 분산 차이 너무 큼 필요 경우에 따라 공분산/상관행렬
변수가 서로 다른 단위(예: cm, kg) 필요 필요 상관행렬

PCA를 구할 때는 우선 변수를 평균 0으로 중심화해야 한다. 또한 변수의 단위가 서로 다르거나 분산 크기가 크게 차이 나는 경우에는 표준화까지 수행해야 한다. 이때 분석은 상관행렬을 기반으로 하게 된다.

(3) 주성분 구하기

데이터 공분산행렬: \(S_{p \times p} = \begin{pmatrix} s_{11} & s_{12} & ... & s_{1p} \\ s_{21} & s_{22} & ... & s_{2p} \\ & ... & & \\ s_{p1} & s_{p2} & ... & s_{pp} \end{pmatrix}\)

데이터 상관계수 행렬: \({\widehat{R}}_{p \times p} = \begin{pmatrix} r_{11} & r_{12} & ... & r_{1p} \\ r_{21} & r_{22} & ... & r_{2p} \\ & ... & & \\ r_{p1} & r_{p2} & ... & r_{pp} \end{pmatrix}\)

공분산행렬(상관계수행렬)은 양반정치(positive definite) 행렬이므로 다음 식을 만족하는 고유값 \(\lambda\)는 0보다 큰 실수이고 행렬의 차수 p개만큼 존재한다.

선형계수 행렬(부하 행렬) \(L_{n \times n}\)에 의해 원 데이터 행렬로부터 주성분 행렬 \(Y_{n \times p} = X_{n \times p}L_{p \times p}\)가 계산된다. 주성분 데이터의 차원은 원데이터 행렬의 차수와 동일하다.

\({\underset{¯}{y}}_{1 \times p} = \left( \begin{array}{r} y_{1} \\ y_{2} \\ ... \\ y_{p} \end{array} \right)\)\(= \begin{pmatrix} l_{11} & l_{12} & ... & l_{1p} \\ l_{21} & l_{22} & ... & l_{2p} \\ & ... & & \\ l_{p1} & l_{p2} & ... & l_{pp} \end{pmatrix}\)\(\left( \begin{array}{r} x_{1} \\ x_{2} \\ ... \\ x_{p} \end{array} \right)\)=\(L\underset{¯}{x}\)

위의 식에 의해 원데이터와 선형계수를 이용하여 계산된 주성분 값을 주성분 점수 score 라 한다.

선형계수 (부하)

공분산행렬 S의 고유벡터 중 \({\underset{¯}{e}}_{i}'\underset{¯}{e} = 1\)을 만족하는 놈(Norm, 정규) 고유벡터를 k-번째 주성분 변수의 선형계수(부하) 벡터 \({\underset{¯}{l}}_{k}\)로 사용한다.

왜 고유벡터(선형계수)를 이용하나?

주성분분석은 데이터가 가장 넓게 퍼져 있는 방향, 즉 분산이 최대가 되는 축을 찾는 것이 목적이다. 공분산행렬은 변수들의 분산과 공분산을 모두 담고 있어 데이터가 어떤 방향으로 크게 퍼져 있는지를 보여주는 지도를 제공한다. 이 공분산행렬을 고유분해하면 고유벡터와 고유값을 얻을 수 있는데, 고유벡터는 데이터가 퍼져 있는 방향을, 고유값은 그 방향으로의 분산 크기를 의미한다.

따라서 가장 큰 고유값에 대응하는 고유벡터는 데이터가 가장 넓게 퍼진 방향이 되고, 이것이 첫 번째 주성분이 된다. 두 번째로 큰 고유값의 고유벡터는 첫 번째 주성분과 직교하면서 남은 분산을 가장 크게 설명하는 방향이 되고, 이렇게 차례대로 주성분들이 정해진다.

결국 주성분을 공분산행렬의 고유벡터로 구하는 것은 우연이 아니라, 주성분분석의 핵심 목표인 ”데이터의 분산을 가장 잘 보존하는 새로운 좌표축”을 찾는 데에 고유벡터가 정확히 그 역할을 하기 때문이다.

제1 주성분 변수

\({\underset{¯}{e}}_{i}'{\underset{¯}{e}}_{i} = 1\)이면서 \(V({\underset{¯}{e}}_{i}'\underset{¯}{x})\)을 최대화 하는 열벡터를 구하고 이를 \({\underset{¯}{l}}_{1}\)이라 하고 이를 선형계수로 하여 제 1 주성분 변수를 구한다. \({\underset{¯}{y}}_{1} = {\underset{¯}{l}}_{1}'\underset{¯}{x}\)

제2 주성분 변수

\({\underset{¯}{l}}_{1}'{\underset{¯}{e}}_{j} = 1\)이면서 \({\underset{¯}{e}}_{j}'{\underset{¯}{e}}_{j} = 1\) 이면서 \(V({\underset{¯}{e}}_{j}'\underset{¯}{x})\)을 최대화 하는 열벡터를 구하고 이를 \({\underset{¯}{l}}_{2}\)이라 하고 이를 선형계수로 하여 제2 주성분변수 \({\underset{¯}{y}}_{2} = {\underset{¯}{l}}_{2}'\underset{¯}{x}\)을 구한다. 이는 제1 주성분 변수와는 서로 독립이고 원변수 변동에 대한 설명력은 제1 주성분 변수보다 낮다.

제3주성분 변수

\({\underset{¯}{l}}_{1}'{\underset{¯}{e}}_{k} = 1\), \({\underset{¯}{l}}_{2}'{\underset{¯}{e}}_{k} = 1\)이면서 \({\underset{¯}{e}}_{k}'{\underset{¯}{e}}_{k} = 1\) 이면서 \(V({\underset{¯}{e}}_{k}'\underset{¯}{x})\)을 최대화 하는 열벡터를 구하고 이를 이를 선형계수로 하여 제3 주성분변수 \({\underset{¯}{y}}_{3} = {\underset{¯}{l}}_{3}'\underset{¯}{x}\)을 구한다. 제3 주성분 변수는 제1, 제2 주성분변수와는 독립이고 변동 설명력은 제1, 제2 주성분 변수보다 낮다. 이렇게 계속 원변수의 개수만큼 주성분변수를 구한다.

공분산 행렬 고유값 및 고유벡터 성질

  • 양반 정치 행렬인 공분산 행렬의 고유치는 모두 양의 실수이고, 원변수의 개수(차수)만큼 존재한다. \(\lambda_{1} \geq \lambda_{2} \geq ...\lambda_{p} \geq 0\)

  • 고유 값이 제일 큰 \(\lambda_1\) 에 의해 만들어지는 주성분변수를 제1 주성분, \(\lambda_2\) 에 의해 만들어지는 주성분 변수를 제2 주성분 변수, 그리고 제3 주성분 변수 … 이다.

  • 고유값 \(\lambda_{k}\)에 대응하는 고유벡터는 무수히 많이 존재하는데 그 중 놈 벡터(\({\underset{¯}{e}}_{k}'{\underset{¯}{e}}_{k} = 1\))를 선형계수 벡터, 부하 벡터로 하여 제 k-주성분 변수, \({\underset{¯}{y}}_{k} = l_k' \underline x\) 을 구한다.

  • 모든 주성분 변수들은 원 변수의 선형 결합이고 서로 독립이다. 이는 모든 고유 벡터(선형계수 벡터)는 서로 독립이 되도록 하여 구하였기 때문이다. 즉, \({\underset{¯}{y}}_{i}'{\underset{¯}{y}}_{j} = 0,fori \neq j\)이다.

  • k-번째 주성분 변수 \({\underset{¯}{y}}_{k}\)의 분산은 \(V({\underset{¯}{y}}_{k}) = \lambda_{k}\)이고 원 변수의 변동합은 고유값의 합과 같다. \(\sigma_{11} + \sigma_{22} + ... + \sigma_{pp} = \lambda_{1} + \lambda_{2} + ... + \lambda_{p}\)

  • 만약 공분산 행렬의 경우 원 변수의 변동합은 상관계수 대각원소(모두 1)의 합이므로 변수의 개수 p가 대각원소 합이므로 \(p = \lambda_{1} + \lambda_{2} + ... + \lambda_{p}\)이다.

  • 그러므로 제k-번째 주성분 변동 기여율은 \(\frac{\lambda_{k}}{\sum_{i = 1}^{p}\lambda_{i}}\)이다. 즉 고유값 \(\lambda_{k}\)는 k-번째 주성분이 원변수들릐 변동을 설명하는 능력이다. 상관계수 행렬의 변동 기여율은 \(\frac{\lambda_{k}}{p}\)이다.

  • 주성분 변수는 원 변수들의 변동을 설명하고 순서대로 설명력은 줄어든다.

시각적 직관

그림 속 원 데이터는 원형에 가깝게 흩어져 있어 X와 Y 변수 간의 상관관계는 거의 0에 가깝다. 두 변수의 분산 역시 동일하기 때문에, 원래 좌표축에서는 특별히 한쪽 축이 더 큰 변동을 설명한다고 보기는 어렵다. 그러나 데이터를 주성분 축으로 회전시키면 상황은 달라진다.

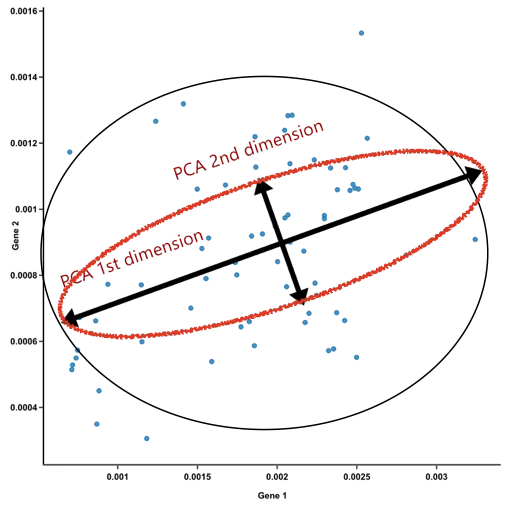
주성분 1과 주성분 2는 서로 직교하는 축이므로 독립적이다. 이때 주성분 1 방향의 분산은 타원의 장축에 해당하며, 주성분 2 방향의 분산은 단축에 해당한다. 따라서 주성분 1이 설명하는 변동성이 주성분 2보다 크다. 즉, 데이터의 구조를 파악하는 데 있어 주성분 1의 설명력이 더 크다고 할 수 있다.

결과적으로 이 경우에는 원래의 두 변수(X, Y)를 모두 사용하는 것과 주성분 1만으로 개체를 설명하는 것 사이에 큰 차이가 없다. 다시 말해, 주성분분석을 통해 얻은 단 하나의 주성분으로도 데이터의 본질적인 분산 구조를 충분히 설명할 수 있다.

(4) 주성분 개수 결정

주성분변수는 원래 변수들의 공분산행렬(혹은 변수 단위가 다른 경우 상관행렬)을 고유분해하여 얻은 고유값과 고유벡터를 바탕으로 구성된다. 각 주성분은 해당 고유값의 크기만큼 원 데이터의 변동을 설명하며, 고유벡터는 주성분을 형성하는 선형계수 역할을 한다. 주성분들은 서로 독립적이며, 제1주성분이 가장 큰 변동을 설명하고, 그다음 제2주성분, 제3주성분 순으로 설명력이 줄어든다. 따라서 주성분의 개수 자체는 원래 변수의 개수와 동일하게 존재한다.

그러나 주성분분석의 본래 목적은 모든 주성분을 다 사용하는 것이 아니다. 주성분분석은 데이터 차원을 줄여서 보다 단순한 구조로 요약하려는 데에 그 의의가 있다. 즉, 원래 변수의 개수가 많더라도 실제로는 누적 설명력이 충분한 일부 주성분만을 선택해 사용함으로써 변수의 차원을 축소하는 것이 주성분분석의 핵심이다.

변동 기여율 기준

주성분분석에서 각 주성분은 원래 데이터의 변동성을 일정 부분 설명한다. 이때 한 주성분이 전체 변동성 가운데 얼마만큼을 차지하는지를 나타내는 비율을 변동 기여율(Explained Variance Ratio)이라 한다.

[공분산행렬] k-번째 주성분변수의 변동설명 기여율(variance explianed ratio) = \(\frac{\lambda_{k}}{\sum_{i}^{p}\lambda_{i}}\)

[상관행렬] k-번째 주성분변수의 변동설명 기여율 = \(\frac{\lambda_{k}}{p}\)

예를 들어 제1주성분의 고유값이 전체 고유값의 합에서 차지하는 비율이 40%라면, 제1주성분이 전체 데이터 변동성의 40%를 설명한다는 의미이다. 또한 변동 기여율을 누적하여 계산하면, 여러 개의 주성분이 함께 전체 변동성을 얼마만큼 설명하는지를 알 수 있다. 이를 누적 변동 기여율이라고 한다. 예를 들어 제1, 제2, 제3주성분까지의 누적 기여율이 85%라면, 이 세 개 주성분만으로도 데이터의 전체 변동성의 85%를 보존할 수 있음을 의미한다.

변동 기여율은 주성분의 개수를 선택할 때 중요한 기준이 된다. 보통 누적 기여율이 일정 수준(예: 70% 이상, 혹은 80~90% 이상)에 도달하는 지점까지만 주성분을 선택한다. 이렇게 하면 원 데이터의 대부분의 정보를 유지하면서도 변수 수를 크게 줄일 수 있다.

【Cochran Rule (Rule of Thumb)】 원변수 변동설명의 누적 기여율이 80%까지 되는 주성분변수까지 선택한다. 즉 20% 정보는 희생된다. 원변수의 상관관계가 높을수록 변수의 차원은 축약이 쉽게되므로 80% 규칙에 의한 주성분변수 개수는 작게 된다.

원 변수들의 상관관계가 높지 않으면 80%를 선택하게 되면 주성분 개수가 많아져 차원 축소가 적어져 일반적으로 주성분은 4개 이상 사용하지는 않는다.

고유값 1이상(Kaiser 기준)

상관행렬을 이용하는 경우 원변수 변동의 합은 p이므로 평균인 1이상 고유값을 갖는 주성분변수만 선택한다. 일반적으로 고유값 1 이상이 주성분을 선택하면 누적 변동설명 기여율 80%와 일치한다.

스크리 플롯(Scree Plot) 방법

고유값의 크기를 순서대로 그래프에 그리면, 설명력이 급격히 감소하다가 완만해지는 지점이 나타난다. 이 꺾이는 부분(엘보 포인트) 이전까지의 주성분을 선택하는 것이 일반적이다. 아래 그림의 스크리 플롯을 기준으로 할 때, 곡선이 꺾이는 지점인 엘보 포인트는 네 번째 주성분 근처에서 나타난다. 따라서 엘보 기준으로 선택되는 주성분의 개수는 4개이다. 반면 Kaiser 기준(고유값이 1보다 큰 경우)을 적용하면 첫 번째, 두 번째, 세 번째 주성분까지만 선택된다. 따라서 이 경우 Kaiser 기준에 따른 주성분 개수는 3개이다.

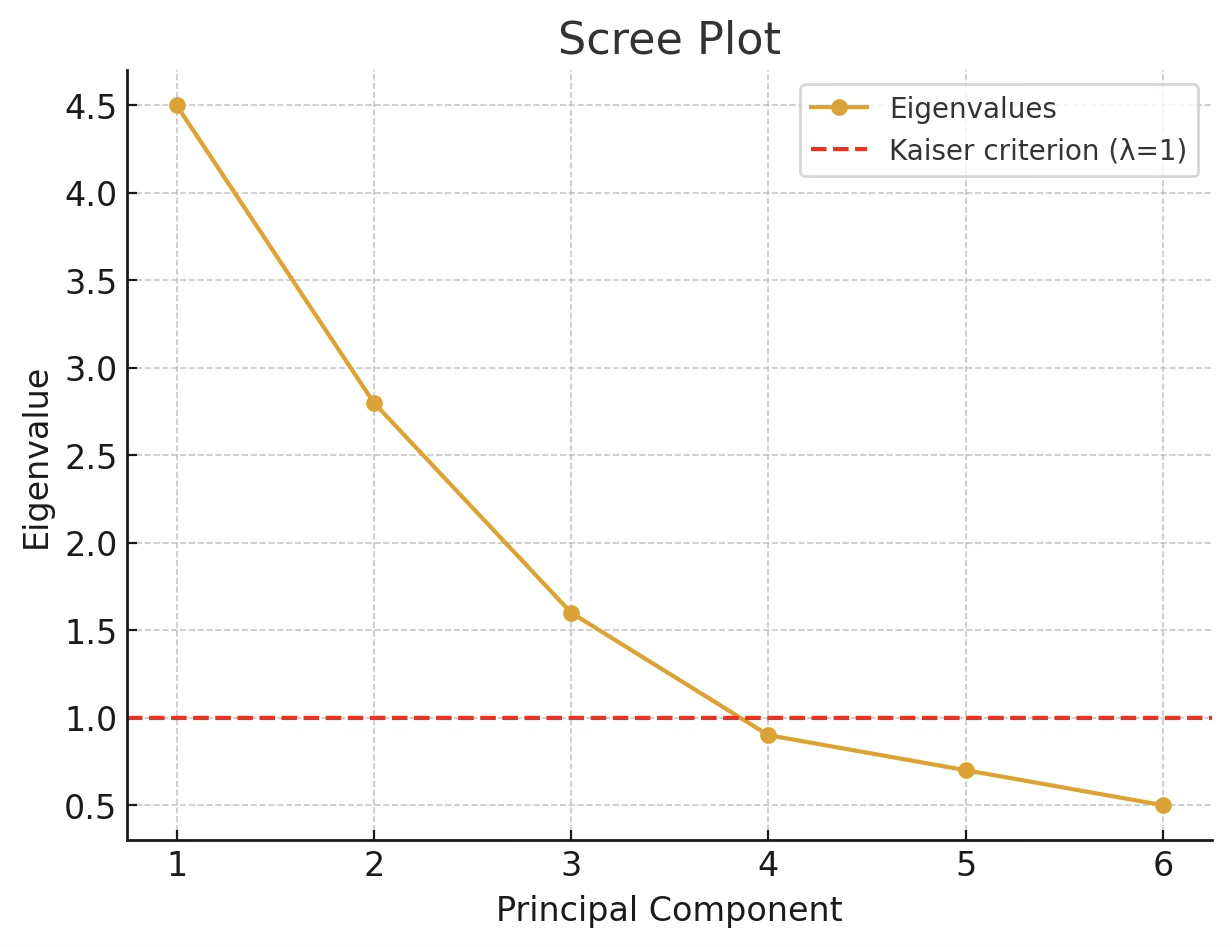
즉, 같은 데이터라도 엘보 기준은 4개, Kaiser 기준은 3개라는 서로 다른 결과를 제시할 수 있으며, 실제 분석에서는 누적 설명 분산비율과 연구 목적까지 함께 고려하여 최종 개수를 결정하게 된다.

(5) 주성분 변수 이름 부여

주성분변수는 원래 변수들의 선형결합으로 정의된다. 즉, 공분산행렬(또는 상관행렬)의 고유벡터를 선형계수로 하여 원 변수를 변환한 것이 주성분변수이다. 이때 각 원 변수의 기여 정도를 나타내는 계수가 바로 부하(loadings)이며, 부하의 절댓값이 클수록 해당 변수가 주성분 형성에 더 큰 영향을 미친다.

따라서 주성분에 이름을 부여하는 과정은, 부하 행렬에서 어떤 변수가 주성분에 강하게 기여하는지를 살펴보고 그 특징을 요약하여 직관적인 이름을 붙이는 것이다.

그러나 이 과정은 결코 단순하지 않다. 하나의 주성분에 여러 변수가 동시에 기여하거나, 서로 해석이 상충되는 부하 값이 섞여 있을 수 있기 때문이다. 또한 부호 방향에 따라 변수 간의 해석이 달라질 수 있고, 실제 데이터의 맥락과 결합해 해석하지 않으면 오해의 소지가 크다.

결국 주성분의 이름 부여는 수학적 계산 결과만으로 자동으로 정해지는 것이 아니라, 연구자가 부하 값의 크기와 방향을 바탕으로 변수군의 공통된 의미를 찾아내는 해석 과정이다. 따라서 단순히 부하의 절댓값만 보는 것이 아니라, 해당 데이터의 맥락과 연구 목적을 종합적으로 고려해야 한다.

즉, 주성분의 이름은 부하 행렬에서 큰 기여를 보이는 변수들의 특성을 요약해 붙이지만, 이는 연구자의 통계적 해석과 도메인 지식이 반드시 결합되어야 하는 작업이다.

3. 주성분 사례분석

(1) Lahman Baseball Database

파이썬의 lahman 모듈은 파이썬에서 메이저리그(MLB) 통계의 표준 데이터베이스인 Lahman Baseball Database를 불러다 쓸 수 있도록 만든 패키지이다.

  • Lahman Baseball Database란? Sean Lahman이 만든 공개 MLB 기록 데이터베이스

  • 1871년부터 최근 시즌까지 선수별/팀별 성적, 경기 기록, 연봉, 올스타, 수상 내역 등을 체계적으로 정리한 자료, 가장 최근 데이터 불러 왔는데 2020년 데이터이다. yearID=2020

  • Lahman DB를 파이썬 pandas DataFrame 형태로 불러오는 간단한 API 제공한다.

batting() → 타자 성적 (연도별, 팀별 기록 포함)
pitching() → 투수 성적
fielding() → 수비 기록
people() → 선수 기본 인적 정보 (이름, 생년월일, 출신국 등)
teams() → 팀별 시즌 기록
salaries() → 연봉 데이터

불러온 데이터프레임은 곧바로 pandas 연산, scikit-learn 모델링, matplotlib 시각화 등에 활용 가능하다.

!pip install lahman #모듈 설치

from lahman import batting, people
import pandas as pd

# 1) 성적 데이터
bat = batting()
latest_year = int(bat['yearID'].max())
bat_latest = bat[bat['yearID'] == latest_year].copy()
bat_latest = bat_latest[bat_latest['AB'].fillna(0) >= 200]

# 2) 이름 데이터
peo = people()

# 필요한 열만 추출 (이름/ID)
peo_names = peo[['playerID','nameFirst','nameLast']]

# 3) merge
bat_with_name = bat_latest.merge(peo_names, on='playerID', how='left')

# 4) 확인
bat_with_name.head()

이하 분석은 200 타석 이상인 66명 타자에 대하여 분석이다.

(2) 상관분석

주성분분석(PCA)은 변수들 간의 상관관계를 토대로 새로운 축을 찾아내어 데이터의 차원을 줄이는 방법이다. 이렇게 도출된 주성분은 다시 개체의 분류나 예측 모델의 설명 변수로 활용되는 등 다양한 2차 분석으로 이어질 수 있다. 따라서 PCA를 수행하기에 앞서 변수들 간의 상관 구조를 사전에 분석하는 것은 매우 중요한 의미를 가진다.

첫째, 상관분석은 변수 간 중복성, 즉 다중공선성의 존재 여부를 파악할 수 있게 해 준다. 주성분분석의 목적은 서로 강하게 연관된 변수들을 요약해 새로운 축으로 재구성하는 데 있다. 만약 변수들 사이의 상관이 거의 없다면 주성분분석을 통해 얻을 수 있는 정보의 압축 효과는 크지 않다. 반대로 변수들이 강하게 상관되어 있다면 소수의 주성분만으로도 전체 변동을 효과적으로 설명할 수 있다. 결국 상관관계의 크기는 PCA를 수행할 가치가 있는지 판단하는 중요한 지표가 된다.

둘째, 상관분석은 변수의 단위 문제를 점검하는 데 도움이 된다. 서로 다른 단위를 가진 변수를 공분산 행렬을 통해 분석하면 단위가 큰 변수가 주성분의 방향을 지배하게 된다. 이때 상관행렬을 사용하면 모든 변수를 표준화한 것과 동일한 효과를 주어 단위 차이를 제거할 수 있다. 따라서 사전 상관분석을 통해 변수 간의 구조를 비교할 때 표준화가 필요한지를 확인할 수 있다.

셋째, 상관분석은 주성분 해석의 방향성을 제공한다. 예를 들어 키와 체중이 강한 양의 상관을 가진다거나, 속도와 시간이 음의 상관을 보인다는 사실은 이후 주성분을 해석할 때 중요한 단서가 된다. 특정 변수들이 함께 움직이는 경향이나 서로 반대 방향으로 움직이는 패턴을 파악해 두면, 추출된 주성분의 의미를 보다 명확하게 해석할 수 있다.

넷째, 상관분석은 불필요한 변수, 즉 노이즈 변수를 걸러내는 데에도 유용하다. 어떤 변수는 다른 변수들과 거의 상관이 없고 독립적으로 움직일 수 있는데, 이런 변수는 전체 구조 요약에 기여도가 낮다. 이 경우 PCA에 포함시키더라도 분석의 효율을 떨어뜨릴 수 있다. 따라서 사전에 상관분석을 실시하면 기여도가 낮은 변수를 미리 파악해 제거함으로써, 보다 간결하고 해석 가능한 주성분 구조를 얻을 수 있다.

이처럼 상관분석은 PCA의 전처리 단계로서 단순한 변수 관계의 탐색을 넘어, 분석 수행의 타당성 점검, 단위 조정 필요성 확인, 주성분 해석의 실마리 제공, 그리고 불필요한 변수 제거를 통한 효율성 제고라는 중요한 역할을 한다고 할 수 있다.

# 1) 분석 변수
cols = ['HR','RBI','SB','BB','SO','H','AB','GIDP']
X = bat_with_name[cols].fillna(0)

# 2) 상관행렬 계산
corr_matrix = X.corr()

# 3) 히트맵 시각화
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(8,6))
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm", fmt=".3f", linewidths=0.5)
plt.title(f"{latest_year} correlation matrix")
plt.show()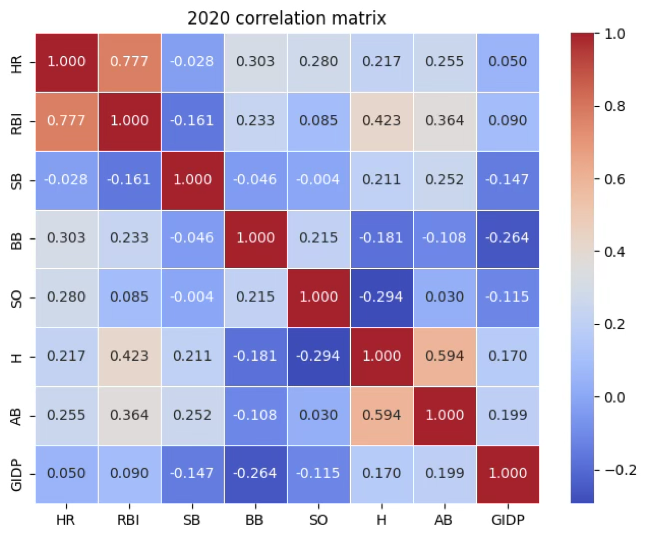

주성분분석을 실시하기 전에 상관행렬을 살펴보면, 변수들 간의 중복성과 구조를 확인할 수 있다. 2020년 타격 지표 상관분석 결과를 보면, 홈런(HR)과 타점(RBI)의 상관계수가 0.777로 매우 높게 나타나는데, 이는 두 지표가 사실상 같은 성향을 반영하고 있음을 의미한다. 따라서 PCA에서는 이 두 변수가 동일한 주성분 축에 강하게 기여할 가능성이 크다. 또한 안타(H)와 타수(AB) 역시 상관계수가 0.594로 높게 나타나, 경기 기회가 많을수록 안타도 많아지는 구조가 반영된 것이다. 이러한 변수 간의 강한 상관은 다중공선성 문제를 드러내며, 바로 PCA를 적용할 필요성을 보여준다.

또한 변수들의 측정 단위가 다르기 때문에, 단위가 큰 변수가 주성분 방향을 지배하지 않도록 상관행렬 기반의 PCA를 활용하는 것이 타당하다. 상관행렬을 사전에 확인하는 과정은 이러한 표준화 필요성을 확인하는 절차가 된다.

상관계수의 패턴은 주성분 해석의 방향성도 제시한다. HR–RBI–BB는 서로 양의 상관을 보이므로 ’장타 및 생산력’ 요인으로 묶일 수 있고, H–AB의 높은 상관은 ’경기 기회와 안타 생산’ 요인을 형성할 수 있다. 한편 삼진(SO)은 안타(H)와 음의 상관(-0.294)을 보이는데, 이는 ’컨택 능력 대 삼진 성향’이라는 대비적 축으로 해석될 수 있다.

마지막으로 상관계수가 전반적으로 낮은 변수들은 노이즈 변수로 볼 수 있다. 병살타(GIDP)는 대부분의 지표와 관련성이 약해 전체 변동 요약에 크게 기여하지 못할 가능성이 크고, 도루(SB) 역시 주요 타격 지표들과는 거의 상관이 없어 별도의 부차적 주성분 축을 형성할 가능성이 있다.

결국 이 상관행렬을 통해 PCA에서 형성될 주성분의 구조를 예측할 수 있다. HR–RBI–BB가 하나의 주성분을, H–AB가 또 다른 주성분을 형성하며, SO는 이와 대립되는 방향의 변동을 설명하고, SB와 GIDP는 부차적이거나 설명력이 낮은 변수로 작용할 것임을 짐작할 수 있다. 이는 곧 PCA가 선수들의 타격 성향을 2~3개의 주성분으로 압축할 수 있음을 보여주는 사전적 근거이다.

(3) 주성분 구하기
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 1) 분석 변수
cols = ['HR','RBI','SB','BB','SO','H','AB','GIDP']
X = bat_with_name[cols].fillna(0)

# 2) 표준화
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# 3) PCA (전체 성분 학습)
pca = PCA()
scores = pca.fit_transform(X_std)

# 3-1) 점수 붙이기
for j in range(scores.shape[1]):
    bat_with_name[f'PC{j+1}'] = scores[:, j]

# 4) 고유값과 Kaiser 필터
eigs = pca.explained_variance_
mask = eigs >= 1
selected_idx = np.where(mask)[0]
selected_eigs = eigs[mask]

# 5) 부하 행렬 (선택된 PC만)
loadings = pd.DataFrame(
    pca.components_.T[:, mask] * np.sqrt(selected_eigs),
    index=cols,
    columns=[f'PC{i+1}' for i in selected_idx]   # ✅ +1 제거!
)

# ✅ 부하 행렬 출력
print("고유값 (전체):", np.round(eigs, 3))
print("선택된 주성분 (λ ≥ 1):", selected_idx+1)
print("부하 행렬 (loadings):")
print(loadings.round(3))

# 6) 각 주성분의 설명 분산 비율
explained_ratio = pca.explained_variance_ratio_

# 7) 누적 설명 분산 비율
cumulative_ratio = np.cumsum(explained_ratio)

# ✅ 출력
print("주성분별 변동 설명 기여율:")
for i, (r, c) in enumerate(zip(explained_ratio, cumulative_ratio), start=1):
    print(f"PC{i}: {r:.3f} (누적 {c:.3f})")

고유값 (전체): [2.423 1.854 1.258 0.945 0.633 0.542 0.306 0.162]
선택된 주성분 (λ ≥ 1): [1 2 3]
부하 행렬 (loadings):
PC1 PC2 PC3
HR 0.776 0.467 -0.070
RBI 0.865 0.282 -0.200
SB 0.090 -0.291 0.838
BB 0.135 0.719 0.186
SO 0.079 0.609 0.175
H 0.696 -0.532 0.122
AB 0.709 -0.371 0.238
GIDP 0.229 -0.403 -0.611

주성분별 변동 설명 기여율:
PC1: 0.298 (누적 0.298)
PC2: 0.228 (누적 0.527)
PC3: 0.155 (누적 0.681)
PC4: 0.116 (누적 0.798)
PC5: 0.078 (누적 0.876)
PC6: 0.067 (누적 0.942)
PC7: 0.038 (누적 0.980)
PC8: 0.020 (누적 1.000)

(4) 주성분 이름부여
#부하 산점도 그리기
import plotly.express as px

# Plotly 산점도 (PC1 vs PC2)
fig = px.scatter(
    loadings.reset_index(),   # index(변수명)를 컬럼으로 복원
    x="PC1",
    y="PC2",
    text="index"              # 변수명을 라벨로 표시
)

fig.update_traces(textposition="top center")
fig.update_layout(title_text="Loading Scatterplot of PC1 and PC2")
fig.show()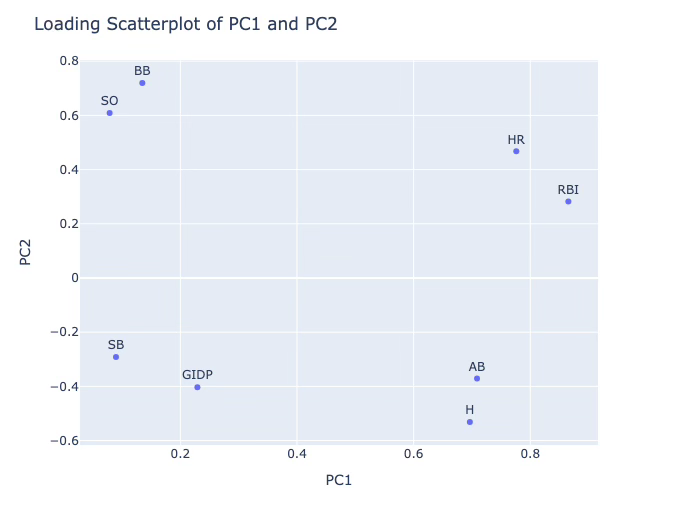

PC1: 파워

  • 높은 부하: RBI (0.865), HR (0.776), H (0.696), AB (0.709) → 타점, 홈런, 안타, 타수 모두 양의 기여.

  • 해석: 타격 생산력과 파워를 반영하는 주성분: ”타격 생산력/파워 성분”

PC2: 선구안

  • 높은 부하: BB (0.719), SO (0.609) (+), HR (0.467)(중간), 음의 부하: H (-0.532), GIDP (-0.403) → 볼넷과 삼진이 동시에 높고, 안타는 음의 방향.

  • 해석: 컨택(안타 중심)과 선구안·삼진 경향의 대비: ”선구안 vs 컨택 성분”

PC3: 주루

  • 높은 부하: SB (0.838) 양수, GIDP (-0.611) 음수 → 도루가 많은 선수일수록 병살타는 적은 경향.

  • 해석: 주루 능력(스피드)을 보여주는 주성분: ”스피드/주루 성분”

(5) 주성분 활용(1) 개체분류
# PC1, PC2 산점도
plt.figure(figsize=(9,7))
plt.scatter(bat_with_name['PC1'], bat_with_name['PC2'], alpha=0.6)

# 선수 이름 표시 (홈런 15개 이상 선수)
for _, row in bat_with_name.iterrows():
    if row['HR'] >= 15:
        plt.text(row['PC1']+0.05, row['PC2']+0.05,
                 f"{row['nameFirst']} {row['nameLast']}", fontsize=8)

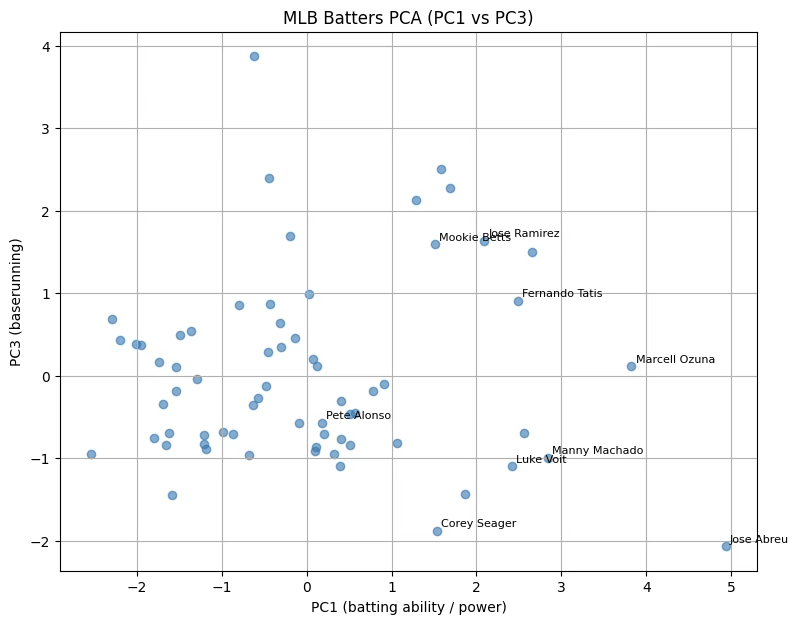
plt.xlabel("PC1 (batting ability / power)")
plt.ylabel("PC2 (plate discipline vs contact)")
plt.title("MLB Batters PCA (PC1 vs PC2)")
plt.grid(True)
plt.show()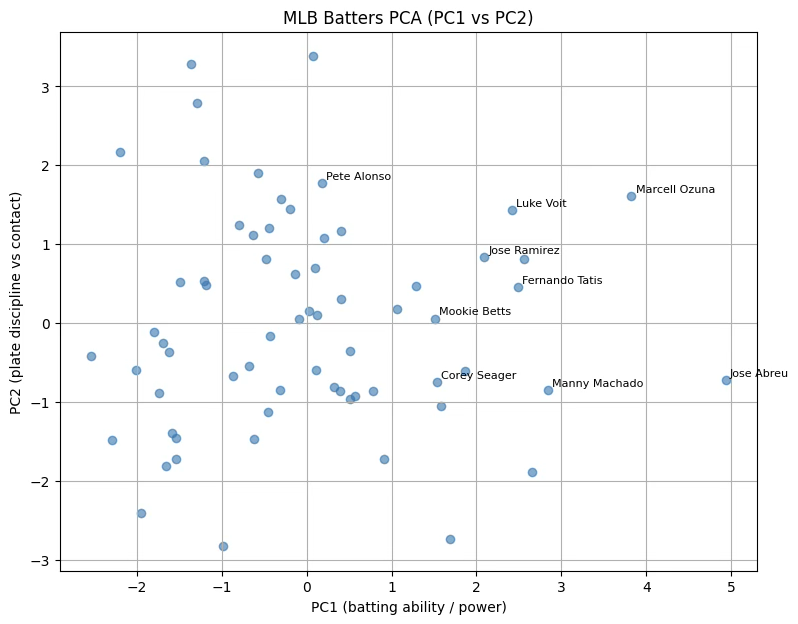

# 각 주성분별 상위 5명 출력
for pc in [‘PC1','PC2','PC3']:
    print(f"\n{pc} 상위 5명:")
    top5 = (bat_with_name[['nameFirst','nameLast','HR','RBI','SB',pc]]
             .sort_values(pc, ascending=False)
             .head(5))
    print(top5.to_string(index=False))

PC1 타격 상위 5명

nameFirst nameLast HR RBI SB PC1
Jose Abreu 19 60.0 0.0 4.934120
Marcell Ozuna 18 56.0 0.0 3.823145
Manny Machado 16 47.0 6.0 2.837655
Trea Turner 12 41.0 12.0 2.651955
Freddie Freeman 13 53.0 2.0 2.554560

PC2 선구안 상위 5명
nameFirst nameLast HR RBI SB PC2
Matt Olson 14 42.0 1.0 3.382615
Christian Yelich 12 22.0 4.0 3.281660
Max Muncy 12 27.0 1.0 2.790429
Yoan Moncada 6 24.0 0.0 2.166739
Carlos Santana 8 30.0 0.0 2.059597

PC3 주루 상위 5명

nameFirst nameLast HR RBI SB PC3
Adalberto Mondesi 6 22.0 24.0 3.875285
Trevor Story 11 28.0 15.0 2.501421
Trent Grisham 10 26.0 10.0 2.397888
Whit Merrifield 9 30.0 12.0 2.271729
Dansby Swanson 10 35.0 5.0 2.135323

(6) 주성분 활용(2) 타자 능력 종합지표

PCA의 큰 장점은 여러 개의 서로 다른 변수들을 중복 없이 압축해 낼 수 있다는 점이다. 예컨대 PCA 결과에서 PC2, PC3, PC4가 각각 파워, 선구안, 그리고 주루 능력을 나타낸다. 그러면 이 세 가지 축은 서로 독립적이면서도 타자의 주요 특성을 대표하는 성분이라고 볼 수 있다.

이때 각 선수의 타격 능력을 하나의 종합 지표로 나타내고 싶다면, 세 성분을 단순 합이 아니라 설명 분산 기여율을 가중치로 반영한 가중합으로 설계할 수 있다. 즉, 각 주성분의 설명력이 큰 만큼 그 성분의 기여도를 더 크게 반영하는 방식이다.

이렇게 하면 최종적으로 얻어지는 PCA-Batting Index는 단일 수치로 선수의 타격 능력을 요약하면서도, 원래 다양한 변수들의 정보를 균형 있게 담아낼 수 있다. 말하자면 OPS나 WAR 같은 전통적 지표와는 다른, 데이터 축약 기반의 통합 평가 지표가 되는 셈이다.

# 선택된 PC 점수만 추출 (예: PC1, PC2, PC3)
selected_pcs = ['PC1','PC2','PC3']
weights = explained_ratio[0:3] / explained_ratio[0:3].sum()  # PC1~PC3 비율 정규화

# 종합 지표 계산
bat_with_name['PCA_Batting_Index'] = (
    bat_with_name[selected_pcs].values @ weights
)

# 상위 10명 확인
print(bat_with_name[['nameFirst','nameLast','HR','RBI','SB','PCA_Batting_Index']]
      .sort_values('PCA_Batting_Index', ascending=False)
      .head(10))

nameFirst nameLast HR RBI SB PCA_Batting_Index
43 Marcell Ozuna 18 56.0 0.0 2.237267
46 Jose Ramirez 17 46.0 10.0 1.567421
59 Fernando Tatis 17 45.0 11.0 1.446034
0 Jose Abreu 19 60.0 0.0 1.446032
63 Luke Voit 22 52.0 0.0 1.287682
22 Freddie Freeman 13 53.0 2.0 1.231654
42 Matt Olson 14 42.0 1.0 1.209545
58 Dansby Swanson 10 35.0 5.0 1.205611
7 Mookie Betts 16 39.0 10.0 1.043342
57 Trevor Story 11 28.0 15.0 0.910111

(7) 주성분 활용(4) 이상치 진단

주성분 분석은 원 변수들의 선형함수를 이용하여 그 변수들의 공분산 구조를 설명하는 방법이다. 표본이 \(n\), 변수 개수가 \(p\)개인 데이터 행렬 로부터의 공분산 행렬을 \(S_{p \times p}\)라 하고, \(\Sigma\)의 고유값을\(\lambda_{1} \geq \cdots \geq \lambda_{p}\), 대응 고유벡터를 \(e_{i}\)라 하자. 고유벡터 \(e_{i}\)를 계수로 하는 원변수의 선형결합 \(y_{i} = e_{i}^{\top}(x - \mu)\)를 i-번째 주성분이라 한다. 다변량 정규 \(x \sim N_{p}(\mu,\Sigma)\)를 가정하면 \(y_{i} \sim N(0,\lambda_{i})\)이며 서로 독립이다.

이상치 진단은 공통 변동을 대표하는 주요 주성분과, 그 밖의 잔차(부) 주성분을 구분하여 수행할 수 있다. 데이터의 전체 변동 중 주요 공통 요인을 설명하는 상위 k개의 주성분을 선택하는 기준은 누적기여율, 스크리 플롯, Kaiser 기준, 병렬분석 등으로 정하는 것이 일반적이다. 이때 Cochran 정리에 의해 정규화된 제곱합은 다음과 같은 카이제곱 분포를 가진다.(Johnson과 Wichern, 2007).

주요 주성분에 의한 이상치 진단 통계량: \(\overset{k}{\sum_{i = 1}}\frac{y_{i}^{2}}{\lambda_{i}} \sim \chi^{2}(k)\)

잔차 주성분에 의한 이상치 발견 통계량: \(\overset{p}{\sum_{i = k + 1}}\frac{y_{i}^{2}}{\lambda_{i}} \sim \chi^{2}(p - k)\)

두 통계량은 서로 독립이다. 첫 번째 통계량은 공통 구조(저차 공간)에서의 이상 행동을, 두 번째 통계량은 공통 구조로 설명되지 않는 잔차 공간에서의 이상 행동을 포착한다. 실무에서는 \(\Sigma\) 대신 표본공분산 S와 표본 고유분해를 사용하므로 분포는 엄밀히 근사이며, 대응 임계값은 경험적 기준 또는 모니터링 기법(Hotelling의 T^2, Q-통계 등)과 함께 사용되는 것이 권장된다.

# === PCA 기반 이상치 진단 ==========================================
from scipy.stats import chi2
import numpy as np
import pandas as pd

# 0) 준비 (위에서 이미 계산된 것들 사용)
# - scores: PCA 점수 (표준화된 X에 대해 학습)
# - eigs:   고유값 (explained_variance_)
# - selected_idx: Kaiser(λ>=1)로 선택된 성분의 인덱스 (0-based)
p = scores.shape[1]
sel = np.array(sorted(selected_idx))                     # 주요 주성분 index
res = np.setdiff1d(np.arange(p), sel)                   # 잔차 주성분 index
k = len(sel)
df_main = k
df_res  = p - k
alpha_main = 0.05
alpha_res  = 0.05

# 1) 정규화된 PC 점수 (각 성분을 표준편차 sqrt(λ)로 나눔)
z = scores / np.sqrt(eigs)                              # shape: (n_samples, p)

# 2) 통계량 계산
T2_main = (z[:, sel]**2).sum(axis=1) if k > 0 else np.zeros(len(z))
T2_res  = (z[:, res]**2).sum(axis=1) if df_res > 0 else np.zeros(len(z))

# 3) 임계값 (카이제곱)
crit_main = chi2.ppf(1 - alpha_main, df_main) if df_main > 0 else np.inf
crit_res  = chi2.ppf(1 - alpha_res,  df_res)  if df_res  > 0 else np.inf

# 4) 데이터프레임에 부착 및 플래그
bat_with_name["T2_main"] = T2_main
bat_with_name["T2_res"]  = T2_res
bat_with_name["flag_main"] = (T2_main > crit_main) if np.isfinite(crit_main) else False
bat_with_name["flag_res"]  = (T2_res  > crit_res)  if np.isfinite(crit_res)  else False
bat_with_name["flag_any"]  = bat_with_name["flag_main"] | bat_with_name["flag_res"]

print(f"[선택 성분 개수 k={k}, df_main={df_main}, df_res={df_res}]")
print(f"임계값(α=0.05): main χ²({df_main})={crit_main:.3f}, residual χ²({df_res})={crit_res:.3f}")

# 5) 상위 이상치 후보 확인 (주요/잔차 각각 상위 10명씩)
top_main = bat_with_name.sort_values("T2_main", ascending=False).head(10)[
    ["nameFirst","nameLast","T2_main","flag_main"]
]
top_res  = bat_with_name.sort_values("T2_res",  ascending=False).head(10)[
    ["nameFirst","nameLast","T2_res","flag_res"]
]

print("\n[주요 주성분 영역 이상치 후보 TOP 10]")
print(top_main.to_string(index=False))
print("\n[잔차 주성분 영역 이상치 후보 TOP 10]")
print(top_res.to_string(index=False))

[선택 성분 개수 k=3, df_main=3, df_res=5]
임계값(α=0.05): main χ²(3)=7.815, residual χ²(5)=11.070

[주요 주성분 영역 이상치 후보 TOP 10]
nameFirst nameLast T2_main flag_main
Jose Abreu 13.735414 True
Adalberto Mondesi 13.266429 True
Whit Merrifield 9.340053 True
Marcell Ozuna 7.434100 False
Christian Yelich 6.806291 False
Trea Turner 6.614026 False
Trevor Story 6.595463 False
Matt Olson 6.206043 False
Trent Grisham 5.437111 False
Hanser Alberto 5.087521 False

[잔차 주성분 영역 이상치 후보 TOP 10]
nameFirst nameLast T2_res flag_res
Cesar Hernandez 15.628843 True
Adalberto Mondesi 14.008599 True
Freddie Freeman 13.942985 True
Javier Baez 11.264646 True
Dansby Swanson 10.582634 False
Carlos Santana 10.357712 False
Tim Anderson 10.154598 False
Kyle Seager 9.084776 False
Kyle Tucker 8.849439 False
Keston Hiura 8.728401 False

# 6) 2D 타원 시각화 (PC1 vs PC2, 95%)
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from scipy.stats import chi2
import numpy as np

# (1) 좌표와 공분산
pcx, pcy = 0, 1                          # 필요시 주성분은 pc1=0, pc2=1, ...
x = scores[:, pcx]
y = scores[:, pcy]
XY = np.column_stack([x, y])
mu = XY.mean(axis=0)
cov = np.cov(XY, rowvar=False)

# (2) 타원 파라미터
vals, vecs = np.linalg.eigh(cov)
order = vals.argsort()[::-1]
vals, vecs = vals[order], vecs[:, order]
chi2_val = chi2.ppf(0.95, df=2)
width, height = 2*np.sqrt(vals*chi2_val)
angle = np.degrees(np.arctan2(*vecs[:,0][::-1]))

# (3) 마할라노비스 거리^2로 이상치 판정(타원 밖)
inv_cov = np.linalg.inv(cov)
d = XY - mu
d2 = np.einsum('ij,jk,ik->i', d, inv_cov, d)            # 거리^2
outlier_mask = d2 > chi2_val

# 4) 플롯 (수정 버전)
fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(x, y, s=25)
ax.scatter(mu[0], mu[1], c='black', s=30)               # 중심점

# 🔧 angle을 keyword argument로 명시!
ellipse = Ellipse(xy=mu, width=width, height=height, angle=angle,
                  edgecolor='orange', facecolor='none', lw=2)
ax.add_patch(ellipse)

# 라벨: 타원 밖만 표시 (playerID 없으면 nameFirst+nameLast 사용)
label_col = 'playerID' if 'playerID' in bat_with_name.columns else None
for i in np.where(outlier_mask)[0]:
    if label_col:
        txt = str(bat_with_name.iloc[i][label_col])
    else:
        txt = f"{bat_with_name.iloc[i]['nameLast']}{bat_with_name.iloc[i]['nameFirst']}"
    ax.text(x[i], y[i]+0.12, txt, fontsize=9)

# 축 라벨: 분산 기여율 표시
vx = pca.explained_variance_ratio_[pcx]*100
vy = pca.explained_variance_ratio_[pcy]*100
ax.set_xlabel(f'PC{pcx+1} component ({vx:.0f}%)')
ax.set_ylabel(f'PC{pcy+1} component ({vy:.0f}%)')
ax.set_title('scatter plot of POWER and Hitting components (Anomaly)')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()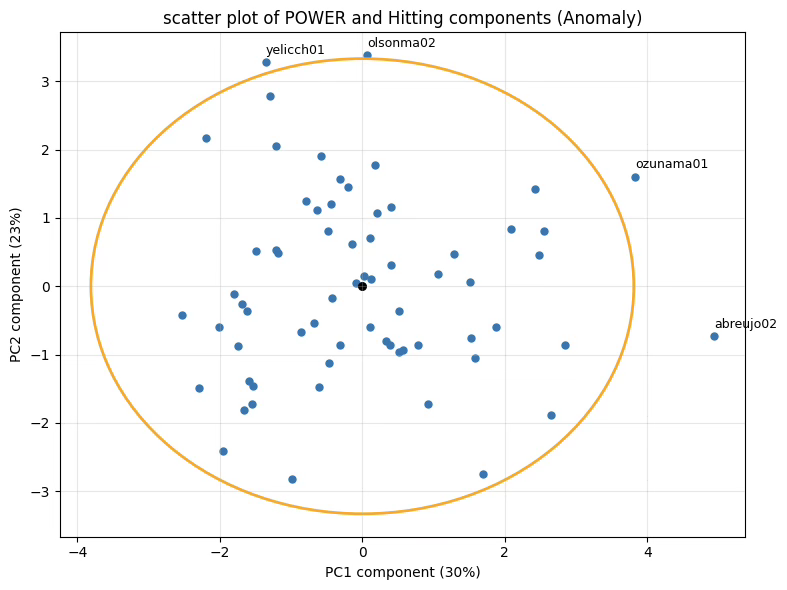

주성분 활용(5) 연봉과 상관관계

연봉과 주성분 점수 간의 관계를 살펴볼 때는 굳이 회귀분석까지 갈 필요는 없는데 이유는 다음과 같다.

연봉은 잡음이 많음: MLB 연봉은 단순히 성적뿐 아니라 나이, 계약 시점, FA·ARB 제도, 포지션, 팀 재정 여건 등 외생 변수가 강하게 작용하여 예측력 지표인 결정계수가 매우 낮아 타격 성적만으로 설명하는 회귀모형은 편향적일 가능성이 크다.

분석 목적이 ”설명력”이 아니라 ”관계 파악”: 분석 목적은 ”어떤 능력(PC2=파워, PC3=선구안, PC4=스피드)이 시장에서 평가받는가?“를 보는 것이므로 상관분석 정도로 충분히 의미를 전달할 수 있다.

연봉 데이터는 2020년 데이터가 없어 타자 능력 데이터와 달리 2016년 데이터를 이용하여 분석 대상 선수는 33명이다(최초 분석 데이터 66명).

from lahman import salaries

# 연봉 데이터 불러오기
sal = salaries()

# 분석 시즌(예: latest_year) 연봉 데이터 선택
sal_latest = sal[sal['yearID'] == 2016] #2020 연봉이 없어 2016년 연봉을 사용

# 선수 이름+PCA 점수 데이터와 연봉 join
bat_with_salary = bat_with_name.merge(
    sal_latest[['playerID','salary']],
    on='playerID',
    how='left'
)

# 결측치 제거
bat_with_salary = bat_with_salary.dropna(subset=['salary'])

# 상관계수 계산 (연봉과 PC 점수)
corrs = bat_with_salary[[‘salary','PC1','PC2','PC3']].corr()

print("연봉과 PCA 성분 상관계수:")
print(corrs['salary'].round(3))

연봉과 PCA 성분 상관계수

salary 1.000
PC1(타격 생산력/파워 성분) 0.074
PC2 (plate discipline vs contact) 0.259
PC3 (speed/baserunning) -0.215

연봉(5salary)–PC1(타격 생산력/파워 성분): +0.074

PC1은 홈런(HR), 타점(RBI), 안타(H) 등 공격 생산력의 공통 변동을 대표하는 성분이다. 상관계수 +0.07은 매우 약한 양(+)의 상관으로, 파워 중심의 성적이 연봉에 일부 긍정적 영향을 주지만, 설명력은 미미하다는 의미이다. 즉, MLB 연봉이 단순히 타격 지표(홈런·타점 등)에 의해 결정되지 않으며, 계약 시기·경력·포지션·수비력 등 복합적 요인이 작용함을 시사한다.

연봉(salary)–PC2(plate discipline vs contact): +0.259

PC2는 볼넷(BB)과 삼진(SO)의 대립 구조로, ”선구안·출루력 vs 컨택 능력”의 대비를 나타내는 축이다. 상관계수 +0.26은 약한 양(+)의 상관으로, 볼넷이 많고 삼진이 적은, 즉 선구안이 좋은 타자일수록 연봉이 높은 경향이 있음을 보여준다. 이는 현대 MLB 시장이 ”출루(OBP)“와 ”타석 퀄리티(plate discipline)”를 일정 부분 보상하고 있음을 시사한다. 다만 0.26 정도면 여전히 제한적 관계이므로, 선구안이 뛰어나도 파워·포지션 프리미엄이 더 큰 영향력을 가질 가능성이 높다.

연봉(salary)–PC3(speed/baserunning): -0.215

PC3은 도루(SB)·주루 능력 등 스피드형 변동을 나타내는 성분이다. 상관계수 -0.22는 음(-)의 약한 상관으로, 주루 능력이 좋은 선수일수록 오히려 연봉이 낮은 경향이 있음을 의미한다. 이는 현대 MLB 시장에서 스피드보다는 파워·출루 중심의 효율적 공격이 더 높은 경제적 가치를 지니는 흐름을 반영한다.

과거 ’도루왕=고액 연봉’의 공식이 이미 무너졌으며, 스피드는 부가적 능력으로만 평가되고 있음을 보여준다. 연봉과 PCA 성분 간의 상관 구조는 전반적으로 약하며, 시장 가치가 특정 기술(파워, 주루, 선구안) 하나로 결정되지 않는다는 점을 드러낸다.

특히 plate discipline(PC2)의 양(+)의 상관이 가장 높게 나타났다는 점은, 최근 MLB에서 ’볼넷 관리 능력’이 점차 중요해지고 있다는 신호로 해석할 수 있다. 결국 연봉은 성적 지표 + 나이 + 계약제도 + 포지션 희소성 + 팀 전략적 필요가 교차하여 형성되는 복합 함수임을 시사한다.

Chapter 3. SVD 차원축소

1. PCA와 SVD 비교

PCA는 원래 변수들 간의 공분산 구조를 분석하여 변수의 수를 줄이는 차원 축소 방법이다.즉, 여러 변수가 내포한 중복된 정보를 제거하고, 분산이 큰 방향으로 축을 회전시켜 소수의 주성분 변수로 요약한다.

반면, SVD는 데이터 행렬 자체를 직교 행렬과 특이값 대각행렬로 분해하는 행렬 분해 기법으로, 변수뿐 아니라 관측치(행) 의 차원까지 함께 축소할 수 있다.

이 때문에 SVD는 데이터의 행과 열을 동시에 저차원 공간으로 표현할 수 있으며, 특히 이미지나 문서처럼 고차원 행렬 데이터를 다루는 기계학습(예: 이미지 분류, LSA 등) 에 널리 활용된다.

PCA는 공분산행렬을 기반으로 하므로 각 주성분의 부하량(loadings) 을 통해 원래 변수들이 주성분에 어떻게 기여하는지를 해석할 수 있지만, SVD는 행렬 전체를 수치적으로 분해하기 때문에 변수의 해석보다는 구조적 압축과 근사에 초점을 둔다.

요약하자면, PCA는 ”변수를 줄이고 해석하는” 통계적 방법이고 SVD는 ”행렬 전체를 축소하고 근사하는” 수학적 방법이다.

2. Sigular Value Decomposition

원데이터 행렬분해
\[X_{n \times p}\] \[=\] \[U_{n \times n}\Sigma_{n \times p}V_{p \times p}\]
(단위 표준화)

\(U\):  특이값 직교행렬
\(\Sigma\) : 대각행렬

\(V\) : 특이값 직교행렬
(1) Full SVD and Reduced SVD

  • \(\Sigma_{n \times p} = \begin{bmatrix} \text{diag}(\sigma_{1},\sigma_{2},\ldots,\sigma_{r}) & 0 \\ 0 & 0 \end{bmatrix}\), 여기서 \(\sigma_{i} = \sqrt{\lambda_{i}}\)(\(X'X\)의 고유치)이며 \(r = \text{rank}(X)\)이다. \(\Sigma_{n \times p}\)은 비대칭 대각행렬이다.

  • \(U'U = I_{n}\): \(U\)가 \(n \times n\) 정사각행렬이면 \(U'U = I_{n}\)이다(Full SVD). 그러나 실제 SVD 계산에서는 보통 Reduced SVD 형태를 사용하므로 \(U\)가 \(n \times r\) 정사각행렬이면 \(U'U = I_{r}\)이다.

  • \(V'V = I_{p}\): 같은 이유로, Reduced SVD에서는 \(V'V = I_{r}\)이다. \(X'X\)의 고유벡터는 \(p \times p\) 행렬 \(V\)의 열로 구성되지만, 실제 계산에서는 \(r\)개의 주축만 사용한다.

(2) Truncated SVD

reduced SVD은 원 데이터 행렬의 계수 r 까지 차원을 줄인다면 Truncated SVD는 그 중에서도 상위 \(k( < r)\)개의 특이값과 대응하는 성분만 남겨, 정보의 손실을 최소화하면서 행렬을 근사하는 방법이다.

즉, 전체 구조를 완전히 복원하는 Reduced SVD와 달리, Truncated SVD는 데이터의 주요 패턴(가장 큰 변동 방향)만 보존하고 미세한 변동이나 노이즈에 해당하는 뒷부분 성분을 버림으로써 데이터를 압축하고 계산 효율을 높이는 목적을 가진다.

\(k\)를 결정할 때는 일반적으로 누적 설명변동 비율(예: 80%)을 기준으로 하므로, 주성분분석에서 차원을 선택하는 방식과 동일하다.

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD

# 1) 변수 선택
cols = ['HR','RBI','SB','BB','SO','H','AB','GIDP']
X = bat_with_name[cols].fillna(0)

# 2) 표준화: 평균 0, 표준편차 1
scaler = StandardScaler()
Z = scaler.fit_transform(X)

# Full SVD: 모든 직교기저 포함
U_full, S_full, Vt_full = np.linalg.svd(Z, full_matrices=True)

print("U_full:", U_full.shape)   # (n, n)
print("S_full:", S_full.shape)   # (min(n, p),)
print("Vt_full:", Vt_full.shape) # (p, p)

# 복원 확인 (완벽하게 동일해야 함)
Z_recon_full = (U_full[:, :len(S_full)] * S_full) @ Vt_full
np.allclose(Z, Z_recon_full, atol=1e-10)

U_full: (66, 66)
S_full: (8,)
Vt_full: (8, 8)
True

# 3) Reduced (Thin) SVD: 정확한 분해
U_r, S_r, Vt_r = np.linalg.svd(Z, full_matrices=False)

# r = rank(Z)
r = len(S_r)

print("rank:", r)   # (Z 행렬 계수)
print("U_r:", U_r.shape)   # (n, n)
print("S_r:", S_r.shape)   # (min(n, p),)
print("Vt_r:", Vt_r.shape) # (p, p)


# 복원 확인
Z_recon = (U_r * S_r) @ Vt_r

rank: 8
U_r: (66, 8)
S_r: (8,)
Vt_r: (8, 8)

# 4) Truncated SVD (상위 k개 성분만 근사)
k = 3
svd_k = TruncatedSVD(n_components=k, random_state=0)
Z_k = svd_k.fit_transform(Z)      # U_k Σ_k
Vk = svd_k.components_            # Vt_k
Sk = svd_k.singular_values_

# 5) 누적 분산비율로 정보량 확인
explained_var = (S_r**2)
ratio = explained_var / explained_var.sum()
cumulative = np.cumsum(ratio)

print(f"Reduced rank r = {r}")
print(f"상위 {k}개 누적 분산 비율: {cumulative[:k]}")

print("Sk:", Sk.shape)   # (min(n, p),)
print("Vk:", Vk.shape) # (p, p)

Reduced rank r = 8
상위 3개 누적 분산 비율: [0.29831468 0.52653148 0.68138709]
Sk: (3,)
Vk: (3, 8)