수리 통계 4. 이변량 확률변수

chapter 1. 확률변수와 확률분포함수

두 개 이상의 확률변수를 포함하는 확률 모형을 다루는데, 이는 자연스럽게 다변량 모형이라고 불린다.

실험적 상황에서 단 하나의 확률변수 값만을 관측하는 것은 매우 이례적일 것이다. 즉, 모든 수집된 데이터가 단 하나의 숫자로 이루어진 실험은 매우 드문 경우이다. 은행 고객이 창구에서 기다리는 시간과 실제로 서비스를 받는 시간은 서로 연관될 수 있다. 대기 시간이 길어지면 서비스 시간이 짧아질 수도 있고, 반대로 복잡한 업무로 인해 서비스 시간이 길어질 경우 대기 시간이 더욱 증가할 수도 있다. 이러한 두 확률변수를 함께 분석하면 은행의 서비스 효율성을 평가하는 데 유용하다.

특정 시간에 바이러스에 감염된 환자 수와 24시간이 지난 후 치료된 환자 수는 상관관계를 가질 수 있다. 예를 들어, 감염 환자가 많을수록 치료된 환자 수도 많을 가능성이 크지만, 치료 속도나 의료 시스템의 효율성에 따라 그 관계는 다르게 나타날 수 있다.

동일한 개체에서 여러 물리적 특성을 측정함으로써 다변량 데이터가 생성될 수도 있다. 예를 들어, 체중뿐만 아니라 체온, 키, 혈압 등의 다양한 건강 지표가 함께 측정될 수 있다. 이와 같이 서로 다른 특성에 대한 측정값들은 각각 개별적인 확률변수로 모델링될 수 있다. 따라서 우리는 두 개 이상의 확률변수를 동시에 다루는 확률 모형을 기술하고 활용하는 방법을 알아야 한다.

이변량 확률변수는 \((X,Y)\)등 알파벳 대문자를 사용하며 다변량 확률변수는 \((X_{1},X_{2},\ldots,X_{n})\) 알파벳 대문자와 아래 첨자를 사용하여 표현한다.

1. 결합 확률밀도함수

\(n\)차원 확률벡터는 표본공간 \(S\)에서 \(\mathbb{R}^{n}\)(즉, \(n\)차원 유클리드 공간)으로 가는 함수이다.

【정의】 이차원 확률벡터는 \((x,y) \in \mathbb{R}^{2}\)(이차원 평면) 된다. 두 개의 주사위를 던지는 실험을 고려하자. 이 실험의 표본공간은 36개의 동일한 확률을 가지는 결과들로 이루어진다.

【예제 ①】 확률변수 \(X\)을 두 주사위 눈금의 합, 확률변수 \(Y\)을 두 주사위 눈금의 차이의 절대값으로 정의하자.

표본점 (4,1)과 (1,4)는 주사위 두 개의 눈이 각각 (4,1) 또는 (1,4)로 나오는 경우이므로 \(P(\{(4,1)\}) = P(\{(1,4)\}) = 1/36\)이다.

\[P(X = 5,Y = 3) = P(\{ 1,4\},\{ 4,1\}) = 1/18\]

위에서 정의된 확률벡터 \((X,Y)\)는 이산확률벡터라고 불린다. 이는 가능한 값들의 개수가 셀 수 있으며(이 경우 유한한 개수) 존재하기 때문이다. 이산확률벡터의 경우 확률밀도함수는 다음과 같다.

\(f(x,y) = P(X = x,Y = y)\).

\((X,Y)\)를 이산형 이변량 확률벡터라고 하자. 이때, 함수 \(f(x,y)\)는 \(\mathbb{R}^{2}\)에서 \(\mathbb{R}\)로 정의되며, 다음과 같이 표현된다.

【정의 이산형】 \(f_{X,Y}(x,y) = P(X = x,Y = y)\) . 이 함수는 이산형 결합확률질량함수(joint probability mass function)라고 불린다.

함수 \(f(x,y)\)가 \(\mathbb{R}^{2}\)에서 \(\mathbb{R}\)로 가는 함수일 때,

【정의 연속형】 이 함수가 연속 이변량 확률벡터 \((X,Y)\)의 연속형 결합확률밀도함수라고 불리려면, 모든 \(A \subset \mathbb{R}^{2}\)에 대해 다음 조건을 만족해야 한다.

\[P((X,Y) \in A) = \int_{A}\int f(x,y)dxdy\]

【예제 ① 계속】 위의 주사위 두 개를 굴리는 경우로 정의된 \((X,Y)\)가 가질 수 있는 21가지 가능한 값이 있다. 이 21가지 가능한 값에 대한 확률, \(f(x,y)\) 값을 정의하는 함수가 결합확률밀도함수이다.

결합확률밀도함수를 이용하면 \((X,Y)\)에 대한 임의의 사건 \(A \subseteq \mathbb{R}^{2}\)에 대한 확률은 \(P((X,Y) \in A) = \sum_{(x,y) \in A}f(x,y)\)이다. 예를 들어, \(A = \{(x,y):x = 7\text{and}y \leq 4\}\)애 대한 확률을 계산해 보자.

\[P(X = 7,Y \leq 4) = P((X,Y) \in A) = f(7,1) + f(7,3) = \frac{1}{18} + \frac{1}{18} = \frac{1}{9}\]

【예제 ① 계속】 \(E(XY)\)을 구하시오.

\(E\lbrack XY\rbrack = (2)(0) \cdot \frac{1}{36} + (4)(0) \cdot \frac{1}{36} + \cdots + (8)(4) \cdot \frac{1}{18} + (7)(5) \cdot \frac{1}{18} = 13\frac{11}{18}\)

\(g_{1}(x,y)\)와 \(g_{2}(x,y)\)가 두 확률밀도함수이고, \(a,b,c\)가 상수일 때 다음의 기대값 합의 연산자가 성립한다.

\[\mathbb{E}\left\lbrack ag_{1}(X,Y) + bg_{2}(X,Y) + c \right\rbrack = a\mathbb{E}\lbrack g_{1}(X,Y)\rbrack + b\mathbb{E}\lbrack g_{2}(X,Y)\rbrack + c\]

【예제 ②】 다음은 두 확률변수 \((X,Y)\)의 결합확률밀도함수, \(f(x,y)\) 이다. \(f(0,0) = f(0,1) = \frac{1}{6},f(1,0) = f(1,1) = \frac{1}{3}.\)

확률계산은 \(P(X = Y) = f(0,0) + f(1,1) = \frac{1}{2}\) 바로 가능하다.

【연속형】 \(\mathbb{E}\lbrack g(X,Y)\rbrack = \int_{- \infty}^{\infty}\int_{- \infty}^{\infty}g(x,y)f(x,y)dxdy\).

2. 주변 확률밀도함수

(1) 이산형

【정리】 이산 이변량 확률벡터 \((X,Y)\)가 결합 확률질량함수 \(f_{X,Y}(x,y)\)를 가진다고 하자. 그러면, \(X\)와 \(Y\)의 주변 확률질량함수(marginal pmf)는 각각 다음과 같이 주어진다.

\[f_{X}(x) = \sum_{y \in \mathbb{R}}f_{X,Y}(x,y),f_{Y}(y) = \sum_{x \in \mathbb{R}}f_{X,Y}(x,y)\]

【예제 ① 계속】 확률변수 \(Y\)의 주변 확률밀도함수는 다음과 같다.

\[f_{Y}(0) = f_{X,Y}(2,0) + f_{X,Y}(4,0) + f_{X,Y}(6,0) + f_{X,Y}(8,0) + f_{X,Y}(10,0) + f_{X,Y}(12,0) = \frac{1}{6}\]

\[f_{Y}(1) = \frac{5}{18},f_{Y}(2) = \frac{2}{9},f_{Y}(3) = \frac{1}{6},f_{Y}(4) = \frac{1}{9},f_{Y}(5) = \frac{1}{18}\]

【예제 ① 계속】 \(P(Y < 3)\)과 \(E(Y^{3})\)을 구하시오.

\[P(Y < 3) = f_{Y}(0) + f_{Y}(1) + f_{Y}(2) = \frac{1}{6} + \frac{5}{18} + \frac{2}{9} = \frac{2}{3}\]

\[\mathbb{E}\lbrack Y^{3}\rbrack = 0^{3}f_{Y}(0) + \cdots + 5^{3}f_{Y}(5) = 20 \cdot \frac{11}{18}\]

(2) 연속형

\(X\)와 \(Y\)의 주변 확률밀도함수는 다음과 같이 주어진다.

\[f_{X}(x) = \int_{- \infty}^{\infty}f(x,y)dy, - \infty < x < \infty,\]

\[f_{Y}(y) = \int_{- \infty}^{\infty}f(x,y)dx, - \infty < y < \infty.\]

【예제 ③】 이변량 확률변수 \((X,Y)\)의 연속형 이변량 확률밀도함수는

\(f(x,y) = \{\begin{matrix} 6xy^{2} & \text{if}0 < x < 1\text{and}0 < y < 1 \\ 0 & \text{otherwise} \end{matrix}\)이다.

\(P(X + Y \geq 1)\) 확률 값은?

\[\begin{matrix} A & = \{(x,y):x + y \geq 1,0 < x < 1,0 < y < 1\} \\ & = \{(x,y):x \geq 1 - y,0 < x < 1,0 < y < 1\} \\ & = \{(x,y):1 - y \leq x < 1,0 < y < 1\} \end{matrix}\]

\[P(X + Y \geq 1) = \int_{A}f(x,y)dxdy = \int_{0}^{1}\int_{1 - y}^{1}6xy^{2}dxdy = \frac{9}{10}\]

【예제 ④】 이변량 확률변수 \((X,Y)\)의 연속형 이변량 확률밀도함수는 \(f(x,y) = e^{- y},0 < x < y < \infty\)이다. \(P(X + Y \geq 1)\)?

\[\begin{matrix} P(X + Y \geq 1) & = 1 - P(X + Y < 1) \\ & = 1 - \int_{0}^{\frac{1}{2}}\int_{x}^{1 - x}e^{- y}dydx \\ & = 1 - \int_{0}^{\frac{1}{2}}\left( e^{- x} - e^{- (1 - x)} \right)dx \\ & = 2e^{- 1/2} - e^{- 1} \end{matrix}\]

3. 조건부 확률밀도함수와 독립

GPA와 SAT 점수가 어느 정도 관련이 있다고 생각할 수 있다. 예를 들어, 어떤 학생이 GPA가 3.9라고 하면, 그의 SAT 점수가 1400 이상일 확률이 높다고 예상할 수 있다. 반면 GPA가 2.0인 학생이라면, SAT 점수가 1400 이상일 가능성은 상대적으로 낮을 수 있다.

즉, GPA(X)를 알고 나면 SAT 점수(Y)의 분포에 대한 정보를 얻을 수 있다는 것인데 이는 조건부 확률 \(P(Y = y \mid X = x)\)으로 표현된다.

【정의 이산형】 \((X,Y)\)가 이산 이변량 확률벡터이고, 결합 확률질량함수가 \(p(x,y)\), \(X\) 주변 확률질량함수가 각각 \(p_{X}(x)\)라고 하자.

\(P(X = x) = p_{X}(x) > 0\)인 임의의 \(x\)에 대해, \(X = x\)라는 정보가 주어졌을 때의 \(Y\)의 조건부 확률질량함수는 다음과 같이 정의된다:

\[p(y|x) = P(Y = y \mid X = x) = \frac{p(x,y)}{p_{X}(x)}\]

【예제 ①】 \((X,Y)\)가 이산 이변량 확률벡터이고, 결합 확률질량함수가 \(p(x,y)\)는 다음과 같다.

\[\begin{matrix} p(0,10) & = p(0,20) = \frac{2}{18},p(1,10) = p(1,30) = \frac{3}{18}, \\ p(1,20) & = \frac{4}{18},p(2,30) = \frac{4}{18}. \end{matrix}\]

\[p_{X}(0) = \frac{4}{18},p_{X}(1) = \frac{10}{18},p_{X}(2) = \frac{4}{18}\]

\(p(10 \mid 0) = \frac{p(0,10)}{p_{X}(0)} = \frac{\frac{2}{18}}{\frac{4}{18}} = \frac{1}{2}\)\(p(20 \mid 0) = \frac{p(0,20)}{p_{X}(0)} = \frac{\frac{2}{18}}{\frac{4}{18}} = \frac{1}{2}\)이다.

\[p(10 \mid 1) = p(20 \mid 1) = 3/10,p(30 \mid 1) = 3/10\]

\[p(30|2) = 1\]

【예제 ②】 이산형 결합 확률밀도함수는 \(p(x,y) = \frac{x + y}{21},x = 1,2,3,y = 1,2\) 이다. \(Y = y\)가 주어졌을 때 확률변수 \(X\) 조건부 확률밀도함수를 구하고 \(P(X = 2|Y = 1)\) 확률을 구하라.

\(Y\) 주변 확률밀도함수 : \(p_{Y}(y) = \sum_{x}^{}{\frac{x + y}{21} = \frac{3y + 6}{21}},y = 1,2\).

\(Y = y\)가 주어졌을 때 확률변수 \(X\) 조건부 확률밀도함수 : \(p\left( x \middle| y \right) = \frac{x + y}{3y + 6},x = 1,2,3wheny = 1,2\).

\(P\left( X = 2 \middle| Y = 1 \right) = \frac{3}{9} = \frac{1}{3}\).

【정의 연속형】 \((X,Y)\)가 연속 이변량 확률벡터이고, 결합 확률질량함수가 \(f(x,y)\), \(X\) 주변 확률질량함수가 각각 \(f_{X}(x)\)라고 하자.

\(f_{X}(x) > 0\)인 임의의 \(x\)에 대해, \(X = x\)라는 정보가 주어졌을 때의 \(Y\)의 조건부 확률질량함수는 다음과 같이 정의된다:

\[f(y|x) = = \frac{f(x,y)}{f_{X}(x)}\]

【예제 ③】 결합 확률밀도함수는 \(f(x,y) = \frac{1}{2},0 \leq x \leq y \leq 2\)이다. \(P(X \leq 1|Y = 2)\) 확률을 구하라.

확률변수 \(Y\) 주변 확률밀도함수 : \(f(y) = \int_{0}^{y}{\frac{1}{2}dx = \frac{x}{2}}\left. \ \right|_{0}^{y} = \frac{y}{2},0 \leq y \leq 2\).

조건부 확률밀도함수 : \(f\left( x \middle| y \right) = \frac{f(x,y)}{f(y)} = \frac{1}{y},,0 \leq x \leq y \leq 2\).

\[P\left( X \leq 1 \middle| Y = 2 \right) = \int_{0}^{1}{f\left( x \middle| y \right)dx =}\int_{0}^{1}{\frac{1}{2}dx = \frac{x}{2}\left. \ \right|_{0}^{1} = \frac{1}{2}}\]

(1) 조건부 기대값 및 분산

【정의 조건부 기대값】 만약 \(g(Y)\)가 Y에 대한 함수라면, \(X = x\)라는 조건 하에서의 \(g(Y)\)의 조건부 기대값은 다음과 같이 정의된다.

\[\mathbb{E}(g(Y) \mid x) = \sum_{y}g(y)f(y \mid x)\text{(이산형 경우)}\]

\[\mathbb{E}(g(Y) \mid x) = \int_{- \infty}^{\infty}g(y)f(y \mid x)dy\text{(연속형 경우)}\]

조건부 분산: \(Var(g(Y) \mid x) = \mathbb{E}((g(Y))^{2} \mid x) - \left( \mathbb{E}(g(Y) \mid x) \right)^{2}\)

【예제 ④】 결합밀도함수: \(f(x,y) = e^{- y},0 < x < y < \infty\)

\(X\)의 주변 확률밀도함수: \(f_{X}(x) = \int_{- \infty}^{\infty}f(x,y)dy = \int_{x}^{\infty}e^{- y}dy = e^{- x}\)

\(Y\)의 조건부 확률밀도함수 : \(f(y \mid x) = \frac{f(x,y)}{f_{X}(x)} = \frac{e^{- y}}{e^{- x}} = e^{- (y - x)},y > x\)

조건부 확률밀도함수는 위치모수 \(\alpha = x\), 척도모수 \(\beta = 1\)인 감마분포이므로 \(\mathbb{E}(g(Y) \mid x) = x\)이다.

(2) 독립

【정의 독립】 \((X,Y)\)를 결합 확률밀도함수 \(f(x,y)\)와 주변 확률함수 \(f_{X}(x),f_{Y}(y)\)를 가지는 이변량 확률벡터라고 하자. 다음을 만족하는 \(X\)와 \(Y\)는 독립 확률변수라고 정의한다.

모든 \(x \in \mathbb{R},y \in \mathbb{R}\)에 대해 \(f(x,y) = f_{X}(x)f_{Y}(y)\)이다.

즉, 결합 확률함수가 두 변수의 주변 확률함수의 곱으로 표현될 수 있으면, 두 변수는 서로 독립이다.

【정리】 \(F_{X,Y}(x,y) = F_{X}\left( x)F_{Y}(y \right)\)이면 두 확률변수 \((X,Y)\)는 서로 독립이고 역도 성립한다.

【정리】 \((X,Y)\) 독립이면 조건부 확률밀도함수는 주변 확률밀도함수와 동일하다. \(p_{X|Y}\left( x|y \right) = p_{X}(x)\), \(f_{X|Y}\left( x \middle| y \right) = f_{X}(x)\).

【정리】 확률변수 \(X\)의 확률 밀도함수는 \(f(x)\), 확률변수 \(Y\)의 확률밀도함수는 \(f(y),y \in S_{Y}\) 이다. 결합 확률밀도함수 \(f(x,y))\)가 두 확률변수의 함수의 곱(\(g(x)h(y)\))으로 표현되고 \(x \in S_{X}\)이고 \(y \in S_{Y}\) (영역이 서로 의존하지 않으면) 두 확률변수 \((X,Y)\)는 서로 독립이고 역도 성립한다. 【필요 충분 조건】

【정리】 \(P(a < X \leq b,c < Y \leq d) = P(a < X \leq b)P(c < X \leq d)\)이면 두 확률변수 \((X,Y)\)는 서로 독립이고 역도 성립한다.

【예제 ①】 결합 확률밀도함수: \(p(x,y) = \frac{x + y}{21},x = 1,2,3,y = 1,2\)두 확률변수는 서로 독립인가?
\(P(X = 1,Y = 1) = \frac{2}{21} \neq P(X = 1)P(Y = 1) = \frac{5}{21}\frac{9}{21} = \frac{45}{21^{2}}\) 독립 아니다.

\(X\) 주변 확률밀도함수 : \(p_{X}(x) = \sum_{y}^{}{\frac{x + y}{21} = \frac{x + 1}{21} + \frac{x + 2}{21}} = \frac{2x + 3}{21},x = 1,2,3\)

\(Y\) 주변 확률밀도함수 : \(p_{Y}(y) = \sum_{x}^{}{\frac{x + y}{21} = \frac{3y + 6}{21}},y = 1,2\)

\(p(x,y) \neq p_{X}(x)p_{Y}(y)\)이므로 독립이 아니다.

【예제 ②】 이변량 결합 확률밀도함수 \(f(x,y) = e^{- (x + y)},0 < x,y\)을 갖는 (\(X,Y\))는 서로 독립인가?

결합 확률밀도함수가 \(g(x) = e^{- x}\), \(h(y) = e^{- y}\)의 곱으로 표현되고 각 영역도 \(S_{X} = \{ x;0 < x\}\)와 \(S_{Y} = \{ y;0 < y\}\) 독립이므로 (\(X,Y\))는 서로 독립이다.

\(X\) 주변 확률밀도함수 : \(f(x) = \int_{0}^{\infty}{e^{- (x + y)}dy} = e^{- x},0 < x\).

\(Y\) 주변 확률밀도함수 : \(f(y) = \int_{0}^{\infty}{e^{- (x + y)}dx} = e^{- y},0 < y\).

\(f(x,y) = f(x)f(y)\)이므로 서로 독립이다.

【예제 ③】 이변량 결합 확률밀도함수 \(f(x,y) = x + y,0 < x,y < 1\)을 갖는 (\(X,Y\))는 서로 독립인가?

결합 확률밀도함수를 \(x\)의 함수와 \(y\)의 함수 곱으로 표현되지 않으므로 (\(X,Y\))는 서로 독립이 아니다.

\(f(x) = \int_{0}^{1}{x + y}dy = x + \frac{1}{2},0 < x < 1\).

\(f(y) = \int_{0}^{1}{x + y}dx = y + \frac{1}{2},0 < y < 1\).

\(f(x,y) \neq f(x)f(y)\)이므로 (\(X,Y\))는 서로 독립이 아니다.

chapter 2. 변수변환

이변량 확률변수 \((X,Y)\)의 함수, \(U = g(X,Y),V = h(X,Y)\)의 확률밀도함수를 구하는 방법에 대하여 살펴보기로 하자.

1. 이산형 이변량 변수변환

이변량 이산형 확률변수 \((X,Y)\)의 결합 확률밀도함수를 \(p_{X,Y}(x,y),(x,y) \in \mathcal{S}\)라 하자. \(u = g(x,y),v = h(x,y)\) 일대일 변환(\(\mathcal{S} \rightarrow \mathcal{T}\))이라 정의하면 이변량 확률변수 \((U,V)\)의 결합밀도함수는 다음과 같다.

\[p_{U,V}(u,v) = p_{X,Y}\left( x = w(u,v),y = z(u,v) \right),(u,v) \in \mathcal{T}where\]

\(x = w(u,v),y = z(u,v)\)은 \(u = g(x,y),v = h(x,y)\)의 일대일 변환 함수이다.

【예제 ①】 이산형 이변량 확률변수 \((X,Y)\)의 결합밀도함수는 \(p(x,y) = \frac{\lambda_{1}^{x}\lambda_{2}^{y}e^{- x}e^{- y}}{x!y!},x,y = 0,1,2,\ldots\)이다. \(U = X + Y\)의 확률밀도함수를 구하라.

1. 이변량 확률변수의 변수 변환이므로 \(U\)변환 이외 관심 변환은 아니지만 간단한 변환변환을 고려하여 \((X,Y) \rightarrow (U,V)\) 이변량 변수 변환을 실시한다.

2. \(U = X + Y,V = Y\)변환을 고려하면 \(X = U - V,Y = V\)이다.

3. \(\mathcal{S} = \left\{ (x,y);x = 0,1,2,\ldots,y = 0,1,2,\ldots \right\}\) ▷ \(\mathcal{T} = \left\{ (u,v);v = 0,1,\ldots,u,v = 0,1,2,\ldots \right\}\)이다.

4. \((U,V)\)의 결합 확률밀도함수는 \(p_{U,V}(u,v) = \frac{\lambda_{1}^{(u - v)}\lambda_{2}^{v}e^{- (\lambda_{1} + \lambda_{2})}}{v!(u - v)!},(u,v) \in \mathcal{T}\)이다.

5. 확률변수 \(U\)에 대한 주변 확률밀도함수를 구하면 된다.\(p_{U}(u) = \sum_{v = 0}^{u}\frac{\lambda_{1}^{(u - v)}\lambda_{2}^{v}e^{- \left( \lambda_{1} + \lambda_{2} \right)}}{v!(u - v)!} = \frac{e^{- \left( \lambda_{1} + \lambda_{2} \right)}}{u!}\sum_{v = 0}^{u}{\frac{u!}{v!(u - v)!}\lambda_{1}^{u - v}\lambda_{2}^{v}}\) \(= \frac{e^{- \left( \lambda_{1} + \lambda_{2} \right)}}{u!}\left( \lambda_{1} + \lambda_{2} \right)^{u} \sim Poisson(\lambda_{1} + \lambda_{2})\).

2. 연속형 이변량 변수변환

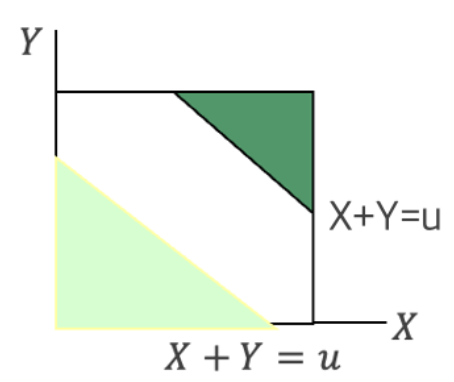
【예제 ②】 이변량 연속형 확률변수 \((X,Y)\)의 결합 확률밀도함수를 \(f(x,y) = 1,0 < x,y < 1\)라 하자. \(U = X + Y\)의 확률밀도함수를 구하라.

1. 확률변수 영역 : \(0 < x,y < 1\)으로부터 \(0 < u < 2\)이다.

2. 만약 \(0 < u \leq 1\), \(F_{U}(u) = P(U \leq u) = P(X + Y \leq u)\)\(= \int_{0}^{u}{\int_{0}^{u - x}{1dydx = \int_{0}^{u}{y\left. \ \right|_{0}^{u - x}dx =}\int_{0}^{u}{(u - x)dx = \frac{u^{2}}{2}}}}\).

3. 만약 \(1 < u < 2\), \(F_{U}(u) = P(U \leq u) = P(X + Y \leq u)\) \(= 1 - \int_{u - 1}^{1}{\int_{u - x}^{1}{1dydx = 1 - \frac{(2 - u)^{2}}{2}}}\).

4. 확률변수 \(U\)의 확률밀도함수는 다음과 같다. \(f_{U}(u) = \left\{ \begin{array}{r} u,0 < u \leq 1 \\ (2 - u),1 < u < 2 \end{array} \right.\ \)

(2) 연속형 이변량 확률변수 Jacobian 방법 이용하기

이변량 연속형 확률변수 \((X,Y)\)의 결합 확률밀도함수를 \(f(x,y),(x,y) \in \mathcal{S}\)라 하자. 이변량 변환 확률변수 \(U = g(X,Y),V = h(X,Y)\)의 결합 확률밀도함수를 \(f(u,v),(u,v) \in \mathcal{T}\)라 정의하고 \(A \in \mathcal{S}\)에 대하여 \(u = g(x,y),v = h(x,y)\) 일대일 변환 함수에 의해 \(B \in \mathcal{T}\)에 대응된다고 하자.

1. 일대일 변환 함수 : \(u = g(x,y),v = h(x,y) \Longleftrightarrow x = w(u,v),y = z(u,v)\)

2. \(J = \left| \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix} \right|\).

3. \(P\left\lbrack (U,V) \in B \right\rbrack = P\left\lbrack (X,Y) \in A \right\rbrack = \int\int f_{X,Y}(x,y)dxdy\).

4. \(f_{U,V}(u,v) = f_{X,Y}\left( w(x,y),z(x,y) \right),(u,v) \in \mathcal{T}\).

【예제 ③】 이변량 연속형 확률변수 \((X,Y)\)의 결합 확률밀도함수를 \(f(x,y) = 1,0 < x,y < 1\)라 하자. \(U = X + Y,V = X - Y\)의 이변량 결합 확률밀도함수를 구하라.

1. 확률변수 \((X,Y)\)의 영역 : \(\mathcal{S} = \{(x,y);0 < x < 1,0 < y < 1\}\)

2. \(U = X + Y,V = X - Y\) 변환 : \(X = \frac{1}{2}(U + V),Y = \frac{1}{2}(U - V)\)

3. \(\mathcal{S} = \{(x,y);0 < x < 1,0 < y < 1\}\) 의 경계 값 확률변수 \((U,V)\)의 영역 \(\mathcal{T} = \{(u,v)\}\) 매핑
   \(x = 0into0 = \frac{1}{2}(u + v)\) \(x = 1into1 = \frac{1}{2}(u + v)\) \(y = 0into0 = \frac{1}{2}(u - v)\) \(y = 1into0 = \frac{1}{2}(u - v)\)

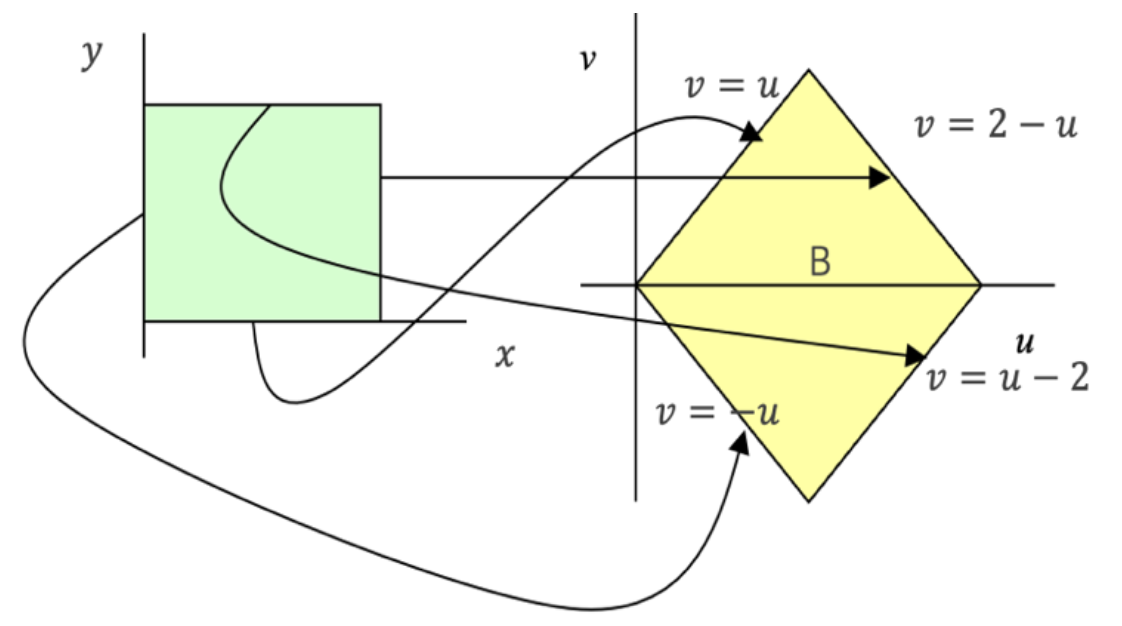
4. Jacobian 구하기 : \(J = \left| \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix} \right| = \left| \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & - \frac{1}{2} \end{matrix} \right| = \left( \frac{1}{2} \right)\left( - \frac{1}{2} \right) - \left( \frac{1}{2} \right)\left( \frac{1}{2} \right) = - \frac{1}{2}\)

5. \(0 < x < 1,0 < y < 1 \leftrightarrow 0 < \frac{1}{2}(u + v) < 1,0 < \frac{1}{2}(u - v) < 1 \leftrightarrow - u < v,v < 2 - u,v < u,u - 2 < v\). 그러므로 \(\mathcal{T} = \{(u,v);u < v,v < 2 - u,v < u,u - 2 < v\}\)

6. \[f_{U,V}(u,v) = f_{X,Y}\left( \frac{1}{2}(u + v),\frac{1}{2}(u - v) \right)|J| = \frac{1}{2},(u,v) \in \mathcal{T}\]

(3) convolution 방법

이변량 결합 확률밀도함수 \(f_{X,Y}(x,y),\mathcal{S} = \{(x,y); - \infty < x,y < \infty\}\)이고 \(U = X + Y,V = Y\) 변환에서 \(U = X + Y\)의 확률밀도함수는 다음과 같다.

\(f_{U}(u) = \int_{- \infty}^{\infty}{f_{X,Y}(u - v,v)dv}\).

【예제 ④】 이변량 결합 확률밀도함수 \(f(x,y) = 2,0 < x < y < 1\)인 경우 \(U = \frac{X}{Y},V = Y\) 이변량 결합 확률밀도함수를 구하시오.

1. \(U = \frac{X}{Y},V = Y\) 변환 : \(X = UV,Y = V\)

2. \[\mathcal{S} = \left\{ (x,y);0 < x,y \right\}\mathcal{} \rightarrow \mathcal{T} = \{(u,v);0 < v < 1,0 < v < 1\}\]

3. \(J = \left| \begin{matrix} V & U \\ 0 & 1 \end{matrix} \right| = UV\)

4. \(f_{U,V}(u,v) = f_{X,Y}(uv,v)|J| = 2v,(u,v) \in \mathcal{T}\)

3. 변수변환에 의한 분포함수의 관계

코쉬 분포

서로 독립인 표준정규분포의 비는 표준 코쉬분포를 따른다.

카이제곱 분포

서로 독립인 정규분포 \(Z_{i} \sim \mathcal{N}(0,1)\)에 대해 \(X = \overset{k}{\sum_{i = 1}}Z_{i}^{2} \sim \chi_{k}^{2}\).

감마 분포

지수분포 \(X_{i} \sim \text{Exp}(\lambda)\)인 n개의 독립 변수 합 \(Y = \overset{n}{\sum_{i = 1}}X_{i} \sim \text{Gamma}(n,\lambda)\).

베타분포

독립인 두 감마분포 변수 \(X \sim \text{Gamma}(\alpha,1),Y \sim \text{Gamma}(\beta,1)\)일 때, \(\frac{X}{X + Y} \sim \text{Beta}(\alpha,\beta)\).

F 분포

독립인 두 카이제곱 변수 \(U \sim \chi_{m}^{2},V \sim \chi_{n}^{2}\)에 대해 \(F = \frac{\frac{U}{m}}{\frac{V}{n}} \sim F_{m,n}\).

t-분포

정규분포 \(Z \sim \mathcal{N}(0,1)\)와 독립된 카이제곱 분포 \(V \sim \chi_{n}^{2}\)를 이용하여 \(T = \frac{Z}{\sqrt{V/n}} \sim t_{n}\).

4. 계층적 모형

어떤 확률변수는 하나의 분포를 갖고 있으며, 그 분포는 어떤 모수에 의존할 수 있다. 일반적으로, 확률변수는 하나의 분포만을 가진다고 보지만, 상황을 계층적으로 바라보는 것이 오히려 더 쉽게 모델링을 가능하게 하는 경우가 많다.

가장 고전적인 계층모형(hierarchical model) 중 하나는 다음과 같다. 한 곤충이 매우 많은 수의 알을 낳고, 각 알은 확률 \(p\)로 생존한다고 하자. 그렇다면 평균적으로 몇 개의 알이 생존하는가? 이때 ”많은 수”의 알은 실제로는 확률변수이며, 흔히 포아송 분포 \(\text{Poisson}(\lambda)\)로 모델링한다. 또한, 각 알의 생존 여부가 독립적이라고 가정하면, 이는 베르누이 시행의 반복이고, 이항분포를 따른다.

낳은 알의 수를 \(Y\), 생존한 알의 수를 \(X\) 라고 하면,

\(X \mid Y \sim \text{Binomial}(Y,p),Y \sim \text{Poisson}(\lambda)\)이다.

\[P(X = x) = \overset{\infty}{\sum_{y = 0}}P(X = x,Y = y) = \overset{\infty}{\sum_{y = 0}}P(X = x \mid Y = y)P(Y = y)\]

\[= \overset{\infty}{\sum_{y = x}}\left\lbrack \binom{y}{x}p^{x}(1 - p)^{y - x} \right\rbrack\left\lbrack \frac{e^{- \lambda}\lambda^{y}}{y!} \right\rbrack\]

이제 이 표현을 단순화하면, \(\frac{\lambda^{x}}{\lambda^{x}}\)로 약분하고 정리하면,

\(P(X = x) = \frac{(\lambda p)^{x}e^{- \lambda}}{x!}\overset{\infty}{\sum_{y = x}}\frac{((1 - p)\lambda)^{y - x}}{(y - x)!}\).

\(t = y - x\) 적용하면, \(P(X = x) = \frac{(\lambda p)^{x}}{x!}e^{- \lambda p} \sim \text{Poisson}(\lambda p)\).

그러므로 \(E(X) = \lambda p\) 생존하는 알의 수이다.

【정리】

\(\mathbb{E}\lbrack X\rbrack = \mathbb{E}\left( \mathbb{E}\lbrack X \mid Y\rbrack \right)\)

\(\mathbb{E}\left( \mathbb{E}\lbrack X \mid Y\rbrack \right) = \mathbb{E}(pY)\) (왜냐하면 \(X|Y \sim B(Y,p)\))

\(\mathbb{E}\left( \mathbb{E}\lbrack X \mid Y\rbrack \right) = \lambda p = \mathbb{E}(X)\) (왜냐하면 \(Y \sim Poisson(\lambda)\))

chapter 3. 기대값

【정의】 이변량 확률변수 \((X,Y)\)의 함수 \(g(X,Y)\) 기대값은 \(E\left( g(X,Y) \right) = \sum_{x}^{}{\sum_{y}^{}{g(X,Y)p(x,y)}}\).\(E\left( g(X,Y) \right) = \int_{x}^{}{\int_{y}^{}{g(X,Y)f(x,y)dydx}}\).

【정리】 이변량 확률변수 \((X,Y)\)가 독립이면\(E(XY) = E(X)E(Y)\)이다.

\(E(XY) = \int\int xyf(x,y)dxdy = (independence)\int\int xyf\left( x)f(y \right)dxdy\)

\(= \int xf(x)dx\int yf(y)dy\) \(= E(X)E(Y)\)

【정리】 이변량 확률변수 \((X,Y)\)가 독립이면 각각의 함수 \(g(X),h(Y)\)에 대해서도 다음이 성립한다.

\(E\left( g(X)h(Y) \right) = E(g(X))E(h(Y))\)이다.

【예제 ①】 결합 확률밀도함수는 \(f(x,y) = 2x,0 \leq x,y \leq 1\) 일 경우 \(E(XY),E(X),V(X)\)을 구하시오.

\[E(XY) = \int\int xyf(x,y)dxdy = \int_{0}^{1}{\int_{0}^{1}{xy(2x)dydx =}}2\int_{0}^{1}{x^{2}\int_{0}^{1}{ydydx =}}2\int_{0}^{1}{x^{2}(\frac{1}{2})dx = \frac{1}{3}}x^{3}\left. \ \right|_{0}^{1} = \frac{1}{3}\]

\[E(X) = \int_{0}^{1}{\int_{0}^{1}{x(2x)dydx =}}2\int_{0}^{1}{x^{2}\int_{0}^{1}{1dydx =}}2\int_{0}^{1}{x^{2}dx = \frac{2}{3}}x^{3}\left. \ \right|_{0}^{1} = \frac{2}{3}\]

\[E(Y) = \int_{0}^{1}{\int_{0}^{1}{y(2x)dydx =}}2\int_{0}^{1}{x\int_{0}^{1}{ydydx =}}2\int_{0}^{1}{x(\frac{1}{2})dx =}\frac{1}{2}x^{2}\left. \ \right|_{0}^{1} = \frac{1}{2}\]

확률변수 \((X,Y)\)가 독립이므로 \(E(XY) = \frac{1}{3} = E(X)E(Y) = \frac{2}{3}\frac{1}{2} = \frac{1}{3}\)

\[E\left( X^{2} \right) = \int_{0}^{1}{\int_{0}^{1}{x^{2}(2x)dydx =}}2\int_{0}^{1}{x^{3}\int_{0}^{1}{1dydx =}}2\int_{0}^{1}{x^{3}dx = \frac{2}{4}}x^{4}\left. \ \right|_{0}^{1} = \frac{1}{2}\]

\[V(X) = E(X^{2}) - E(X)^{2} = \frac{1}{2} - \left( \frac{2}{3} \right)^{2} = \frac{1}{18}\]

【예제 ②】 결합 확률밀도함수는 \(f(x,y) = 8xy,0 < x < y < 1\) 일 경우 \(E\left( XY^{2} \right),E(Y),E(\frac{X}{Y})\)을 구하시오.

\(E\left( X^{2}Y \right) = \int_{0}^{1}{\int_{0}^{y}{xy^{2}(8xy)dxdy =}}\int_{0}^{1}{\frac{8}{3}y^{6}dy =}\frac{8}{21}\).

\(E(Y) = \int_{0}^{1}{\int_{0}^{y}{y(8xy)dxdy =}}\int_{0}^{1}{y\left( 4y^{3} \right)dy =}\frac{4}{5}\).

\(U = \frac{X}{Y}\)라 놓자. \(U\)의 확률분포함수 \(F_{U}(u) = P(U \leq u) = P(X \leq uY) = \int_{0}^{1}{\int_{0}^{uy}{8xydxdy = \int_{0}^{1}{4u^{2}y^{3}dy = u^{2},0 < u < 1}}}\)이다. 그러므로 \(f(u) = F_{U}'(u) = 2u,0 < u < 1\)이다.

\(E\left( U = \frac{X}{Y} \right) = \int_{0}^{1}udu = \frac{2}{3}\).

【예제 ③】 결합 확률밀도함수는 \(f(x,y) = 3x,0 \leq y \leq x \leq 1\) 일 경우 \(E(X - Y)\)을 구하시오.

\(E(X) = \int_{0}^{1}{\int_{0}^{x}{x(3x)dydx = \int_{0}^{1}{3x^{2}(x)dx = \frac{3}{4}x^{4}\left. \ \right|_{0}^{1} = \frac{3}{4}}}}\).

\[E(Y) = \int_{0}^{1}{\int_{0}^{x}{y(3x)dydx = \int_{0}^{1}{3x\left( \frac{1}{2}x^{2} \right)dx = \frac{3}{2}(\frac{1}{4}x^{4})\left. \ \right|_{0}^{1} = \frac{3}{8}}}}\]

\(E(X - Y) = E(X) - E(Y) = \frac{3}{4} - \frac{3}{8} = \frac{3}{8}\).

\[E(X - Y) = \int_{0}^{1}{\int_{0}^{x}{(x - y)3xdydx =}}\int_{0}^{1}{\int_{0}^{x}{(x - y)3xdydx =}}\int_{0}^{1}{\int_{0}^{x}{x3xdydx - \int_{0}^{1}{\int_{0}^{x}{yxdydx =}\frac{3}{4} - \frac{3}{8} = \frac{3}{8}}}}\]

【정의】 이변량 확률변수 벡터 \(\overline{X} = (X,Y)'\)의 기대값 벡터는 \(E\left( \overline{X} \right) = \lbrack\begin{array}{r} E(X) \\ E(Y) \end{array}\rbrack\)이다.

【예제 ④】 결합 확률밀도함수는 \(f(x,y) = 3x,0 \leq y \leq x \leq 1\) 일 경우 \(E\)(\(\lbrack\begin{array}{r} X \\ Y \end{array}\rbrack\))을 구하라.

\(E(X) = \int_{0}^{1}{\int_{0}^{x}{x(3x)dydx = \int_{0}^{1}{3x^{2}(x)dx = \frac{3}{4}x^{4}\left. \ \right|_{0}^{1} = \frac{3}{4}}}}\).

\(E(Y) = \int_{0}^{1}{\int_{0}^{x}{y(3x)dydx = \int_{0}^{1}{3x\left( \frac{1}{2}x^{2} \right)dx = \frac{3}{2}(\frac{1}{4}x^{4})\left. \ \right|_{0}^{1} = \frac{3}{8}}}}\).

\(E\)(\(\lbrack\begin{array}{r} X \\ Y \end{array}\rbrack\))= \(\lbrack\begin{array}{r} 3/4 \\ 3/8 \end{array}\rbrack\) (차수가 2인 열 벡터임)

【정의】 이변량 확률변수 \((X,Y)\)에서 \(X = x\)가 주어졌을 때 \(Y\)의 조건부 기대값 \(E\left( Y \middle| x \right) = \int yf_{Y|X}\left( y \middle| x \right)dy = \frac{\int yf(x,y)dy}{f_{X}(x)},y \in \mathcal{S}_{Y}\)

【예제 ⑤】 결합 확률밀도함수는 \(f(x,y) = 2,0 < x < y < 1\)이다. \(E\left( Y \middle| x \right),V(Y|x)\)을 구하라.

\(f(x) = \int_{y}^{1}{2dy} = 2(1 - x),0 < x < 1\)

\[f\left( y \middle| x \right) = \frac{f(x,y)}{f(x)} = \frac{2}{2(1 - x)} = \frac{1}{1 - x},0 < x < y < 1\]

\[E\left( Y \middle| x \right) = \int_{x}^{1}{\frac{1}{1 - x}ydy = \frac{1}{2(1 - x)}}y^{2}\left. \ \right|_{x}^{1} = \frac{1 + x}{2},0 < x < 1\]

\[E\left( Y^{2} \middle| x \right) = \int_{x}^{1}{\frac{1}{1 - x}y^{2}dy = \frac{1}{3(1 - x)}}y^{3}\left. \ \right|_{x}^{1} = \frac{x^{2} + x + 1}{3},0 < x < 1\]

\(V\left( Y^{} \middle| x \right) = \frac{x^{2} + x + 1}{3} - \left( \frac{1 + x}{2} \right)^{2}\)

【정리】 이변량 확률변수 \((X,Y)\)에 대하여 다음이 성립한다.

\((a)E(E(Y|X)) = E(Y)\)

\((b)V(E(Y|X)) = V(Y)\)

【예제 ⑥】 결합 확률밀도함수는 \(f(x,y) = 6y,0 < y < x < 1\)이다. 위의 정리를 보여라.

확률변수 \(Y\)주변 확률밀도함수 : \(f(y) = \int_{y}^{1}{6ydx} = (6y)x\left. \ \right|_{y}^{1} = 6y(1 - y),0 < y < 1\)

\[E(Y) = \int y(6y(1 - y))dy = 6\left( \frac{1}{3}y^{3} - \frac{1}{4}y^{4} \right)\left. \ \right|_{0}^{1} = \frac{1}{2}\]

확률변수 \(X\)주변 확률밀도함수 : \(f(x) = \int_{0}^{x}{6ydx} = 3x^{2},0 < y < 1\)

\(X = x\)가 주어졌을 때 \(Y\)의 조건부 확률밀도함수 : \(f\left( y \middle| x \right) = \frac{6y}{3x^{2}} = \frac{2y}{x^{2}},0 < y < x < 1\)

\(X = x\)가 주어졌을 때 \(Y\)의 조건부 기대값 : \(E\left( Y \middle| x \right) = \int_{0}^{x}{y\left( \frac{2y}{x^{2}} \right)dy = \frac{2}{3}x,0 < x < 1}\).

\(E\left( Y \middle| x \right) = \frac{2}{3}X\)는 확률변수이므로 \(U = g(X) = \frac{2}{3}X\)의 확률밀도함수를 구해야 \(E(E\left( Y|x \right))\) 기대값을 구할 수 있다. \(0 < x < 1 \rightarrow 0 < u < \frac{2}{3}\) 이고\(X = \frac{3}{2}U\)이다.

\(\frac{2}{3}X\)는 증가 함수이므로 \(f_{X}(u) = f\left( x = \frac{3}{2}u \right)|J| = 3\left( \frac{3}{2}u \right)^{2}\left| \frac{3}{2} \right| = \frac{81}{8}u^{2},0 < u < \frac{2}{3}\)

그러므로 \(E\left( E\left( Y \middle| x \right) \right) = \int_{0}^{\frac{2}{3}}{u\left( \frac{81}{8}u^{2} \right)du = \frac{81}{8*4}u^{4}\left. \ \right|_{0}^{\frac{2}{3}} = \frac{1}{2}}\).

chapter 4. 상관계수

두 확률변수 간의 직선적(선형) 관계의 정도를 측정하는 지표로 공분산(covariance) 이 사용된다. 하지만 공분산은 각 변수의 단위(scale)에 영향을 받기 때문에, 이를 비교 가능하도록 변수의 표준편차로 나눈 값을 상관계수(correlation coefficient) 라 한다.

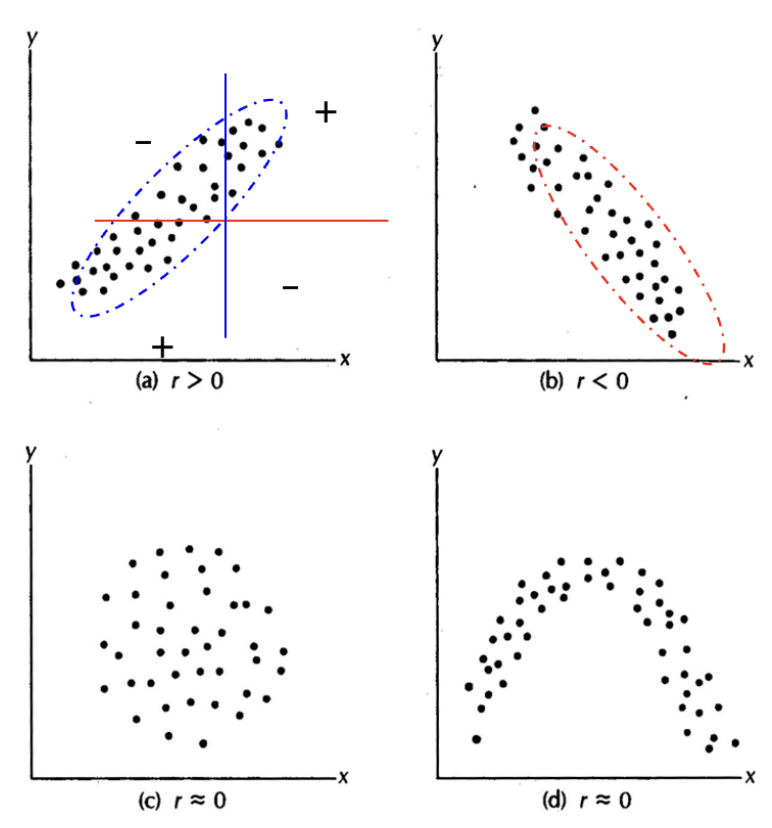
상관계수는 단위에 무관하며, 두 변수 사이의 선형 관계의 강도와 방향을 -1에서 1 사이의 값으로 나타낸다.

선형(직선) 관계

상관계수는 두 변수 사이의 선형 관계를 측정하는 지표로, 두 변수가 일정한 비율로 함께 증가하거나 감소할 때 높은 값을 갖는다. 그러나 두 변수 간에 비선형적인 관계가 존재하는 경우, 상관계수는 이러한 관계를 적절히 반영하지 못할 수 있다. 따라서 상관계수는 선형성 가정 하에서만 해석하는 것이 적절하며, 비선형 관계를 탐색할 때는 다른 분석 도구가 필요하다.

범위

상관계수의 값은 -1에서 1 사이의 범위를 가지며, 이 값은 두 변수 사이의 선형 관계의 방향과 강도를 나타낸다. 상관계수가 1에 가까울수록 두 변수는 같은 방향으로 강하게 함께 움직이며, 이는 완전한 양의 선형 관계를 의미한다. 반대로 상관계수가 -1에 가까울수록 두 변수는 서로 반대 방향으로 강하게 움직이며, 이는 완전한 음의 선형 관계를 뜻한다. 상관계수가 0이면 두 변수 사이에 선형적인 관련성은 없다고 해석할 수 있다. 다만, 상관계수가 0이라 하더라도 비선형적인 형태의 관계가 존재할 수 있으므로, 상관계수만으로 변수 간 관계를 전부 설명할 수 있는 것은 아니다.

부호

상관계수의 부호는 두 변수 간 관계의 방향을 나타낸다. 상관계수가 양수일 경우, 한 변수가 증가할 때 다른 변수도 함께 증가하는 양의 관계가 존재함을 의미한다. 반대로 상관계수가 음수이면, 한 변수가 증가할 때 다른 변수는 감소하는 음의 관계가 있음을 뜻한다. 이처럼 상관계수의 부호는 변수 간의 변화 방향이 서로 같은지 혹은 반대인지를 판단하는 데 중요한 정보를 제공한다.

무작위성

상관계수는 두 변수 간의 선형적인 관련성만을 측정할 뿐, 인과관계를 입증하는 지표는 아니다. 즉, 두 변수 사이에 높은 상관관계가 나타난다고 해서 한 변수가 다른 변수에 영향을 준다고 단정할 수는 없다. 상관관계는 단지 두 변수 간에 일정한 방향성과 강도로 변화가 함께 나타나는 경향을 보여줄 뿐이며, 이러한 관계가 우연인지, 제3의 변수에 의한 것인지, 혹은 실제 인과관계인지는 별도의 분석과 검증을 통해 확인해야 한다.

【정의】 확률변수 \(X\)의 기대값과 분산을 \(E(X),V(X)\), 확률변수 \(Y\)의 기대값과 분산을 \(E(Y),V(Y)\)라 하자. 이변량 확률변수 \((X,Y)\)의 공변량 covariance는 다음과 같이 정의한다. \(COV(X,Y) = E\left( \left( X - E(X) \right)\left( Y - E(Y) \right) \right)\).

【정의】 이변량 확률변수 \((X,Y)\)의 상관계수correlation coefficient는 다음과 같이 정의한다.

\(\rho = \frac{COV(X,Y)}{\sqrt{V(X)}\sqrt{V(Y)}}\).

상관계수 해석

공분산 간편식

\(COV(X,Y) = E\left( \left( X - E(X) \right)\left( Y - E(Y) \right) \right) = E(XY) - E(X)E(Y)\)만약 두 확률변수가 서로 독립이면 공분산은 0이다. 그러나 역은 성립하지 않는다. 즉, 공분산이 0이어도 서로 독립이 아닐 수 있다.

\(E(XY) = \int\int xyf(x,y)dxdy = \left( \because indepentf(x,y) = f(x)f(y) \right)\)

\(= \int xf(x)dx\int yf(y)dy = E(X)E(Y)\) 이므로 \(COV(X,Y) = 0\).

【예제 ①】 결합 확률밀도함수는 \(f(x,y) = 3x,0 \leq y \leq x \leq 1\) 일 경우 공분산 \(COV(X,Y)\)을 구하라.

\[E(XY) = \int_{0}^{1}{\int_{0}^{x}{xy(3x)dydx = \int_{0}^{1}{3x^{2}\left( \frac{1}{2}x^{2} \right)dx = \frac{3}{10}5\left. \ \right|_{0}^{1} = \frac{3}{10}}}}\]

\[E(X) = \int_{0}^{1}{\int_{0}^{x}{x(3x)dydx = \int_{0}^{1}{3x^{2}(x)dx = \frac{3}{4}x^{4}\left. \ \right|_{0}^{1} = \frac{3}{4}}}}\]

\[E(Y) = \int_{0}^{1}{\int_{0}^{x}{y(3x)dydx = \int_{0}^{1}{3x\left( \frac{1}{2}x^{2} \right)dx = \frac{3}{2}(\frac{1}{4}x^{4})\left. \ \right|_{0}^{1} = \frac{3}{8}}}}\]

\(COV(X,Y) = \frac{3}{10} - \left( \frac{3}{4} \right)\left( \frac{3}{8} \right) = \frac{3}{160}\).

【예제 ②】 결합 확률밀도함수는 \(f(x,y) = x + y,0 \leq x,y \leq 1\) 일 경우 상관계수 \(corr(X,Y)\)을 구하라.

\[E(XY) = \int_{0}^{1}{\int_{0}^{1}{xy(x + y)dxdy = \int_{0}^{1}{\frac{1}{3}y + \frac{1}{2}y^{2}dy = \frac{1}{6}y^{2} + \frac{1}{6}y^{3}\left. \ \right|_{0}^{1} = \frac{1}{3}}}}\]

\[E(X) = \int_{0}^{1}{\int_{0}^{1}{x(x + y)dxdy = \int_{0}^{1}{\frac{1}{3} + \frac{1}{2}ydy = \frac{1}{3}y + \frac{1}{4}y^{2}\left. \ \right|_{0}^{1} = \frac{7}{12}}}}\]

\[E\left( X^{2} \right) = \int_{0}^{1}{\int_{0}^{1}{x^{2}(x + y)dxdy = \int_{0}^{1}{\frac{1}{4} + \frac{1}{3}ydy = \frac{1}{4}y + \frac{1}{6}y\left. \ \right|_{0}^{1} = \frac{5}{12}}}}\]

\[V(X) = E\left( X^{2} \right) - E(X)^{2} = \frac{5}{12} - \left( \frac{7}{12} \right)^{2} = \frac{11}{144}\]

동일하게 \(E(Y) = \frac{7}{12}\), \(V(Y) = \frac{11}{144}\)

\[COV(X,Y) = \frac{7}{12}\frac{7}{12} - \frac{48}{144} = \frac{1}{144}\]\[corr(X,Y) = \rho = \frac{COV(X,Y)}{\sqrt{}V(X)\sqrt{}V(Y)} = \frac{\frac{1}{144}}{\frac{11}{144}} = 1/11\]

【예제 ③】 다음은 공분산은 0이지만 서로 독립은 아니다.

\(X\) \(Y\)	0	1	2	주변 합
0	1/16	3/16	1/16	5/16
1	3/16	0	3/16	6/16
2	1/16	3/16	1/16	5/16
주변 합	5/16	6/16	5/16	1

\(E(X) = 0*\frac{5}{16} + 1*\frac{6}{16} + 2*2*\frac{5}{16} = 1\), \(E(Y) = 1\)

\(E(XY) = (0)(0)\frac{1}{16} + (0)(1)\frac{1}{16} + \ldots + (1)(2)\frac{1}{16} = 1\).

그러므로 \(COV(X,Y) = E(XY) - E(X)E(Y) = 1 - 1 = 0\)\(P(X = 0,Y = 0) = \frac{1}{16} \neq P(X = 0)P(Y = 0) = \frac{5}{16}\frac{5}{16}\) 독립이 아니다.

【정리】 이변량 확률변수 \((X,Y)\)의 평균과 분산을 각각 \(\left( \mu_{X},\mu_{Y} \right),(\sigma_{X}^{2},\sigma_{Y}^{2})\)라 하고 상관계수를 \(\rho\)라 하자. \(E\left( Y \middle| x \right)\)는 확률변수 \(X\)의 선형함수이다. \(E\left( Y \middle| X \right) = \mu_{Y} + \rho\frac{\sigma_{Y}}{\sigma_{X}}(X - \mu_{X})\).

그리고 \(E\left( V(Y) \middle| X \right) = \sigma_{Y}^{2}(1 - \rho^{2})\).

【예제 ④】 결합 확률밀도함수는 \(f(x,y) = 2,0 \leq x \leq y \leq 1\)이다. \(E(Y|x)\)을 구하라.

\(\int_{x}^{1}{y(2)dy = y^{2}\left. \ \right|_{x}^{1} = 1 - x^{2} = (1 - x)(1 + x)}\).

확률변수 \(X\) 주변 확률밀도함수 : \(f(x) = \int_{x}^{1}{2dy = 2y}\left. \ \right|_{x}^{1} = 2(1 - x),0 \leq x \leq 1\).

\(E\left( Y \middle| x \right) = \frac{(1 - x)(1 + x)}{2(1 - x)} = \frac{1 + x}{2}\).

chapter 5. 다변량 확률변수

1. 개념

【정의】 확률실험의 표본공간을 \(\mathcal{S}\)에서 정의된 \(n\)개의 확률변수 \(X_{i}(w) = x_{i},i = 1,2,\ldots,n,w \in \mathcal{S}\)에 대하여 다음을 n-차 랜덤 벡터라 정의한다.

랜덤 벡터: \(\overline{X} = (X_{1},X_{2},\ldots,X_{n})'\)

영역:\(\mathcal{D} = \{\left( x_{1},x_{2},\ldots,x_{n} \right);x_{1} = X_{1}(w),X_{2}(w),\ldots,x_{n} = X_{n}(w),w \in \mathcal{S}\}\)

다변량 확률 분포함수 \(F_{\overline{X}}\left( \overline{x} \right) = P(X_{1} \leq x_{1},X_{2} \leq x_{2},\ldots,X_{n} \leq x_{n})\)

다변량 결합 확률밀도함수

(연속형) \(f_{\overline{x}}\left( \overline{x} \right) = \frac{\partial^{n}}{\partial x_{1}\partial x_{2}\ldots\partial x_{n}}F_{\overline{x}}\left( \overline{x} \right) = f(x_{1},x_{2},\ldots,x_{n})\)

(이산형) \(p_{\overline{x}}\left( \overline{x} \right) = p(x_{1},x_{2},\ldots,x_{n})\)

【정의】 확률변수 \((X_{1},X_{2},\ldots,X_{n})\)의 함수 \(U = g(X_{1},X_{2},\ldots,X_{n})\)(확률변수) 기대값은 다음과 같이 정의된다.

(연속형) \(E(U) = \int\int\cdots\int uf\left( x_{1},x_{2},\ldots,x_{n} \right)dx_{1}dx_{2}\ldots dx_{n}\)

(이산형) \(E(U) = \sum_{x_{1}}^{}{\sum_{x_{2}\cdots}^{}{\sum_{x_{n}}^{}{p(x_{1},x_{2},\ldots,x_{n})}}}\)

【정의】 동일한 모집단 분포 \(f(x)\)으로부터 서로 독립적으로 추출한 크기 \(n\)인 표본 \((X_{1},X_{2},\ldots,X_{n})\)을 확률표본이라 한다.

확률변수 \(X_{i}\)의 확률 밀도함수 :\(f\left( x_{i} \right) = f(x)\) (동일한 모집단 분포)

\((X_{1},X_{2},\ldots,X_{n})\) 결합 확률밀도함수 :

\(f\left( x_{1},x_{2},\ldots,x_{n} \right) = (iid)f\left( x_{1} \right)f\left( x_{2} \right)\ldots f\left( x_{n} \right) = f(x)^{n}\)

【정의】 확률표본 \((X_{1},X_{2},\ldots,X_{n})\)의 평균은 \((\mu_{1},\mu_{2},\ldots,\mu_{n})\), 분산은 \((\sigma_{1}^{2},\sigma_{2}^{2},\ldots,\sigma_{n}^{2})\)인 경우 확률표본의 선형함수 \(U = \sum_{i}^{n}{a_{i}X}_{i}\)의 평균은 \(\sum_{i}^{n}{a_{i}\mu_{i}}\)이고 분산은 \(\sum_{i}^{n}{a_{i}^{2}\sigma_{i}^{2}}\)이다. 단, \(a_{i}\)는 상수이다.

【정리】 확률표본 \((X_{1},X_{2},\ldots,X_{n})\)의 선형함수 \(U = \sum_{i}^{n}{a_{i}X}_{i}\)의 적률생성함수는 다음과 같다. \(M_{\sum_{i}^{}{a_{i}X_{i}}}(t) = \prod_{i}^{n}{M_{X_{i}}(a_{i}t)}\).

2. 공분산 행렬

랜덤 확률 벡터 \(\overline{X} = (X_{1},X_{2},\ldots,X_{n})'\)의 평균 벡터와 공분산 행렬은 다음과 같이 정의된다.

기호 : \(E\left( X_{i} \right) = \mu_{i},\)

\(COV\left( X_{i},Y_{j} \right) = \sigma_{ij} = E\left( X_{i} - \mu_{i} \right)\left( X_{j} - \mu_{j} \right) = \sigma_{ji}fori \neq j,\sigma_{ii} = \sigma_{i}^{2}fori = j\)

랜덤 확률변수 벡터 : \(\overline{X} = \left\lbrack \begin{array}{r} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \end{array} \right\rbrack\)

평균 벡터 : \(E(\overline{X}) = \left\lbrack \begin{array}{r} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{n} \end{array} \right\rbrack\)

공분산 행렬 : \(COV\left( \overline{X} \right) = \Sigma = \begin{pmatrix} \sigma_{ii} & \cdots & \sigma_{in} \\ \vdots & \ddots & \vdots \\ \sigma_{ni} & \cdots & \sigma_{nn} \end{pmatrix}\)

【정리】 만약 \(X_{i}\)가 서로 독립이면 공분산이 0이므로 공분산 행렬은 대각원소가 분산인 대각 행렬이다.

\(COV(\overline{X}) = \begin{pmatrix} \sigma_{ii} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{nn} \end{pmatrix}\)

【정의】 \(\overline{X} \sim (E\left( \overline{X} \right) = \overline{\mu},COV\left( \overline{X} \right) = \Sigma)\)이고 \(\overline{a} = (a_{1}a_{2}\ldots a_{n})'\)이 상수 벡터인 경우 다음이 성립하다.

\(E\left( {\overline{a}}'\overline{X} \right) = {\overline{a}}'\overline{\mu} = \sum_{i}^{n}{a_{i}\mu_{i}}\).

\(COV\left( {\overline{a}}'\overline{X} \right) = {\overline{a}}'COV(\overline{X})\overline{a} = {\overline{a}}'\Sigma\overline{a}\).

【정리】 \(X_{i} \sim iidN(\mu_{i},\sigma_{i}^{2})\)이면\(\sum_{i}^{n}{a_{i}X_{i} \sim N(\sum_{i}^{n}{a_{i}\mu_{i}},\sum_{i}^{n}{a_{i}^{2}\sigma_{i}^{2}})}\)

\(X_{i} \sim N(\mu_{i},\sigma_{i}^{2})\) 적률생성함수 : \(M_{X_{i}}(t) = exp(\mu_{i}t + \frac{\sigma_{i}^{2}t^{2}}{2})\)

\[{M_{\sum_{i}^{n}a_{i}X}}_{i}(t) = \prod_{i}^{n}{M_{X_{i}}(a_{i}t)} = \prod_{n}^{n}{\exp\left( \mu_{i}(a_{i}t) + \frac{\sigma_{i}^{2}{(a_{i}t)}^{2}}{2} \right)} = \exp\left( \sum_{i}^{n}{{(\mu}_{i}a_{i}})t + \frac{\sum_{i}^{n}{{(\sigma}_{i}^{2}{a_{i})t}^{2}}}{2} \right)\]

그러므로 \(\sum_{i}^{n}{a_{i}X_{i} \sim N(\sum_{i}^{n}{a_{i}\mu_{i}},\sum_{i}^{n}{a_{i}^{2}\sigma_{i}^{2}})}\)

【정리】 \(X \sim iidN(\mu,\sigma^{2})\)의 확률표본\((X_{1},X_{2},\ldots,X_{n})\)의 평균 \(\frac{\sum_{i}^{n}X_{i}}{n} \sim N(\mu,\frac{\sigma^{2}}{n})\)이다.

【정리】 \(X \sim iidN(\mu,\sigma^{2})\)의 확률표본\((X_{1},X_{2},\ldots,X_{n})\)의 분산 \(S^{2} = \frac{\sum_{i}^{n}\left( X_{i} - \overline{X} \right)^{2}}{n - 1}\)이면 \(\frac{(n - 1)S^{2}}{\sigma^{2}} \sim \chi^{2}(n - 1)\).

【정리】 위의 2 정리를 통합하면 다음과 같다. \(X \sim iidN(\mu,\sigma^{2})\)의 확률표본\((X_{1},X_{2},\ldots,X_{n})\)의 평균 \(\overset{¯}{X} = \frac{\sum_{i}^{n}X_{i}}{n}\), 분산 \(S^{2} = \frac{\sum_{i}^{n}\left( X_{i} - \overline{X} \right)^{2}}{n - 1}\)에 대하여 다음이 성립한다.

표본평균 \(\overline{X}\), 표본분산 \(S^{2}\) 서로 독립이다.

\(\overset{¯}{X} \sim N(\mu,\frac{\sigma^{2}}{n})\).

\(\frac{(n - 1)S^{2}}{\sigma^{2}} \sim \chi^{2}(n - 1)\).